一种三维仿真中服装搭配穿透问题解决方法与流程

本发明涉及三维仿真技术领域，特别是涉及一种Unity3D环境下的服装仿真穿透问题解决方法。

背景技术：

服装仿真是三维仿真技术领域中一个重要的技术方向。随着虚拟现实技术和服装电子商务的快速发展，更真实、更高效的服装仿真技术能够提供客户更加真实的服装购买体验。目前主流的服装仿真技术有弹簧质点模型、骨骼蒙皮等。这些技术能够很好的解决服装在物理和动作环境中的服装状态问题，但是服装模型的不均匀会产生服装搭配之间多件服装之间的网格穿透问题。

多件服装之间的网格穿透会导致服装仿真效果不真实，影响仿真效果。传统解决服装穿透问题大多采用递归查找和射线求交的方法。这些方法能够求出两个服装网格之间的相交网格，但计算量很大不适用于移动端。

技术实现要素：

为了克服上述现有技术的不足，本发明提供了一种三维仿真中服装搭配穿透问题的解决方法。本发明旨在通过较低计算量来解决多件服装之间搭配时的网格穿透问题，使服装仿真更加真实。

本发明所采用的技术方案是：

一种三维服装搭配穿透问题解决方法，包括Unity 3D环境下局部透明着色器、服装模型重叠部分计算及透明方法。

其中，Unity 3D环境下局部透明着色器部分，其特征在于，包含：

通过Unity 3D下ShaderLab语言编写局部透明着色器。该着色器能够通过一张带有特定透明通道的贴图，将该贴图映射至模型UV空间，再通过Shader渲染，使得模型中由贴图透明通道为0的部分透明，实现模型局部透明效果。由于Unity 3D中具有透明通道的着色器渲染时会产生深度错误，所以本发明通过使用不同的pass，达到深度测试的正常化。具体实现方法如下：

1、通过多通道语言结构来人为控制渲染顺序。2、采用双pass的渲染顺序来实现控制渲染顺序：第一个pass实现对back部分网格的渲染，同时叠加透明通道。第二个pass实现对front部分网格的渲染，同时叠加透明通道。

对于，服装模型重叠部分计算及透明方法，其特征在于，包含：

本发明提出的方法针对不同的服装类型和不同的服装层次做出不同的处理方法，达到的最优效果。对于同时穿上上衣和裤子的情况，上衣的穿戴层次较裤子大，所以需要处理裤子穿透上衣部分的网格。这一部分的处理方法如下：

首先查找到上衣下边缘的边缘最高点。由于服装边缘是不规则的曲线，且服装面片具有不连续性，要查找到边缘最高点不能使用传统找边缘的方法来寻找边缘最高点。本发明使用按角度切割，查找角度最低点的方法查找到近似的边缘最高点。按角度切割面片首先需要将面片中的顶点坐标由笛卡尔坐标系转换为极坐标系，再由极坐标系中按角度进行分割。笛卡尔坐标系转换为极坐标系中需要进行转换计算，将原坐标系中转换为 ,极坐标中极坐标中，xoz平面中的半径值，值为xoz平面中的角度值。转化公式为：

转化后在极坐标空间中，通过判断一个角度范围 中的y 值，找到该范围中的最小值，当前的值为局部最小值。找到所有范围中的值 ，求出所有的最大值，即可求出对应的上衣下边缘的最大值的逼近值。

上述判断一个角度范围。由于服装网格布局具有不确定性，每一个角度范围的局部最小值不一定是服装的下边缘顶点值。为了保证查找算法的鲁棒性，本发明专利提出了一个经验值，即在每60度角度中查找局部最小值。找到下边缘的最大值的逼近值后，需要求出裤子被上衣遮住的部分网格。将之前查找出的上衣最大值的逼近值，求出裤子网格中高于该值的面片，同时记录三角面片中的三个顶点的UV坐标值。为避免覆盖部分网格穿透，本发明提出将被覆盖网格透明化处理的思路，由于穿透的网格透明度为0，所以避免了裤子网格穿透遮住了上衣网格。

上述将裤子模型被覆盖网格透明化处理，通过计算被覆盖网格UV空间所对应的贴图方位透明通道置零实现。通过三角形向量计算算法，计算出被覆盖的网格UV空间对应的区域。

上述计算被覆盖网格UV空间，其方法为：

当找到裤子被上衣覆盖的顶点之后，查找对应的点的UV空间坐标。将这部分顶点视为一个点集，同时这部分点在UV空间中所映射点所包围的若干区域视为待透明区域。将三角顶点映射至UV空间，并将在UV空间中的坐标值扩展至二维透明贴图空间。即 ,W为透明贴图宽度，H为透明贴图高度。将三角面片中三个点在透明贴图空间求出最小包围盒，求出包围盒中所有贴图像素是否在三角形内。如果在三角形内则透明化，如果不在则不透明。将所有在三角面片中的点视为一个集合，该集合就是上述透明贴图中的透明区域。对于同时穿上上衣和裤子的情况，当裤子穿戴层次较上衣大，上衣穿透裤子部分网格。这一部分的处理方法如下：

首先查找到裤子上边缘最低点，其方法为：

转换裤子网格顶点的笛卡尔坐标系至三维极坐标系。将笛卡尔坐标系中 ，转换为 ，给定一个角度区间将面片进行切分，在该角度区间中找到局部高度最大值。将按照角度切分的网格局部高度最大值集合求出该集合中的最小值，将该值视为裤子上边缘的逼近最小值，将逼近最小值作为参数，将衣服模型网格中低于该值的所有面片视为一个集合。由于衣服网格较为复杂，所以需要进行面片过滤，将除服装躯干部分网格过滤。

上述所说面片过滤计算，其方法为：1、区分子网格。如果一个三角形与另一个三角形有两个顶点索引值相同，这认为两个三角形相连，求出两个三角面片组成的小网格的包围盒。2、网格过滤。求出所有相连的三角面片，可以组成若干个较大的三角网格，同时求出该网格的矩形包围盒。对比矩形包围盒中心点，根据服装模型躯干中心经验值进行过滤得到躯干部分网格。

上述服装模型躯干中心经验值，本发明提出为0.2。根据Unity 3D中单位转换，该值为20dm。将三角顶点映射至UV空间，并将在UV空间中的坐标值扩展至二维透明贴图空间。即 ,W为透明贴图宽度，H为透明贴图高度。计算出三角面片在透明贴图空间中的矩形包围盒。通过三角形向量计算算法，对比矩形包围盒中每一个像素点是否在三角形中，若点在三角形中则透明化如果不在则不透明。

上述计算贴图像素是否在三角形内，采用三角形向量计算算法，其方法为：求出点P与三角形一点A的向量AP，与该点和其他三角形顶点B,C 的向量 ,如果所得向量在同一方向，返回为真。分别求出是否在同一边,以及所得结果是否在同一边，如果三次计算都在同一边,认定该点在三角形中。

与现有技术相比，本发明的有益效果是：1、计算模型之间相交部分的计算量与计算时间，能够很好的适用于手机等计算能力较低的移动端。2、将透明部分的渲染交给gpu渲染，提高整个方法的效率。3、采用包围盒计算方法，极大减少计算量。4、在视觉上，减少服装层次之间的面片穿透，提高用户体验。

附图说明

图1为服装搭配穿透问题解决方案流程简图。

图2为服装搭配穿透问题解决方法流程图。

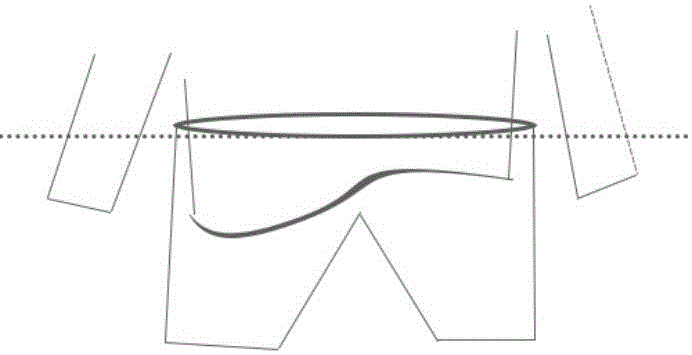
图3为裤子模型层次比衣服模型大的情况。

图4为衣服模型层次比裤子模型大的情况。

图5为上衣模型过滤示意图。

具体实施方式

为了使本发明实现的技术手段、创作特征、达成目的与功效易于明白了解，下面进一步阐述本发明。

本发明效果基于Unity 3D游戏引擎实现。Unity3D游戏引擎以其快速开发能力被众多游戏开发者接受，同时Unity 3D基于3D计算引擎OpenGL等，适合虚拟仿真、虚拟现实等应用开发，也适合3D图形学、3D计算机仿真等实验开发。

本发明中所提到的算法分为上衣层次高于裤子、裤子层次高于上衣两方面对服装上下衣的穿透进行处理。如图1所示，图1表示本发明所提出的服装穿透解决方法。在输入上衣和裤子模型后，确定两个模型所在的层次关系，如果上衣层次较裤子层次高，则上衣模型在显示时需要覆盖裤子模型，则需要确定裤子模型的透明区域。如果裤子层次较上衣层次高，则裤子模型在显示时需要部分覆盖上衣模型，则需要确定上衣模型的透明区域。当上衣层次较裤子层次高时：首先初始化网格模型，通过Unity 3D接口获取到上衣模型网格顶点数据，和裤子模型网格顶点数据。当初始化模型数据完成后，先通过坐标转化公式将上衣顶点坐标所对应的笛卡尔坐标系，转换为极坐标系。由于Unity 3D中坐标系为右手系，所以转换为极坐标系的平面为XOZ平面。将原笛卡尔坐标系中 ，x,z值转化为极坐标系。坐标系转换公式如下：

在转换后坐标系中，代表该点与中心轴连接的向量与x轴所成角度夹角，代表点离中心点的半径。通过对顶点进行角度划分就能找到在同一角度下的顶点的集合。找到同一角度范围中的顶点的集合就能实现将网格竖直分割，从而避免服装的复杂性。

转化后在极坐标空间中，通过判断一个角度范围中的值，找到该范围中的最小值，当前的值为局部最小值。由于不同服装模型网格布局的复杂性，往往查找的最小值是衣服下边缘的顶点最小值。为了提高本发明中提出的查找最低点算法的鲁棒性，本发明中提供一个角度经验值。即在每的角度空间中查找一个最小值。通过遍历一个圆周中所有的角度范围，找到所有范围中的值，求出所有的最大值，即可求出对应的上衣下边缘的最大值的逼近值，该值接近于衣服下边缘的最大值。

查找到上衣下边缘的最大值的逼近值后，需要求出裤子被上衣遮住的部分网格。首先将初始化所得到的裤子模型网格数据获取，通过遍历与上衣下边缘的值进行对比，查找空间坐标系中y值到高于的所有裤子网格面片，将所有的查找的面片视为同一集合，同时记录所有顶点的UV坐标值。

将查找到的面片集合中的顶点所对应的UV空间中的坐标值扩展至透明贴图空间中,W为透明贴图的宽度值，H为透明贴图的高度值。扩展函数为：。找到不同模型顶点所对应的贴图空间坐标值后，将单个面片的三个顶点在贴图空间中的坐标值记录，并查找到三角面片的x最大值 最小值 ，y的最大 最小值 ，通过这四个值构建三角形的矩形包围盒 ，。w为包围盒的宽，h为包围盒的高。遍历该包围盒中所有像素值，判断是否在三角形中。

本发明专利使用三角形向量算法求出像素值是否在三角面片映射在透明贴图的二维三角形中。首先遍历包围盒中所有像素点，假设有像素点P，求出点P与三角形一点A的向量AP，与该点和其他三角形顶点B,C 的向量 ,如果所得向量在同一方向，返回为真。分别求出是否在同一边，以及所得结果是否在同一边，如果三次计算都在同一边，认定该点在三角形中。

将计算在三角形中的每个像素点所在的透明通道值设为0。将所有被遮盖的三角形所对应的UV空间中的透明通道设为0。在渲染时将被遮盖三角形网格透明化，即可避免裤子网格穿透上衣网格。

当裤子模型层次高于上衣层次时：首先初始化网格模型，通过unity3D接口获取到裤子、上衣网格模型的顶点和面片数据。

将上述获取的裤子面片数据获取后，首先将面片默认的笛卡尔坐标系转化成极坐标系。将笛卡尔坐标系中，转换为，给定一个角度区间将面片进行切分，在该角度区间中找到局部高度最大值。将按照角度切分的网格局部高度最大值集合求出该集合中的最小值，将该值视为裤子上边缘的逼近最小值。将最小值的逼近值作为参数将衣服模型网格中低于该值的所有面片视为一个集合。之后将这个点面集合中除躯干部分网格进行过滤。

上述所说的面片过滤计算，其流程为：1、区分子网格。如果一个三角形与另一个三角形有两个顶点索引值相同，这认为两个三角形相连。求出两个三角面片组成的小网格的包围盒。2、网格过滤。求出所有相连的三角面片，可以组成若干个较大的三角网格，同时求出该网格的矩形包围盒。对比矩形包围盒中心点，根据服装模型躯干中心经验值进行过滤得到躯干部分网格。

上述服装模型躯干中心经验值，本发明提出为0.2。根据Unity 3D中单位转换，该值为20dm。将查找到的面片集合中的顶点所对应的UV空间中的坐标值[0,1]扩展至透明贴图空间中 ,W为透明贴图的宽度值，H为透明贴图的高度值。扩展函数为： 找到不同模型顶点所对应的贴图空间坐标值后，将单个面片的三个顶点在贴图空间中的坐标值记录，并查找到三角面片的x最大值最小值，y的最大值最小值，通过这四个值构建三角形的矩形包围盒，。w为包围盒的宽，h为包围盒的高。遍历该包围盒中所有像素值，判断是否在三角形中。

通过上述三角形向量计算算法，对比矩形包围盒中每一个像素点是否在三角形中，若点在三角形中则透明化如果不在则不透明。