一种改进的K_MEANS算法对解决制造业物料采购问题的制作方法

本发明涉及企业管理领域，具体地涉及用算法解决制造业物料采购问题。

背景技术：

随着全球市场一体化以及信息时代的到来，企业采购的比重大大增加。在全球范围内，工业企业的产品构成中，采购的原料以及零部件成本平均水平在60％以上。从世界范围来说，对于一个典型的企业，采购成本(包括原材料，零部件)要占60％。而在中国的工业企业，各种物资的采购成本要占到企业销售成本的70％。显然采购成本是企业管理中的主体和核心部分，采购是企业管理中“最有价值”的部分。另外，根据国家经贸委1999年发布的有关数据，如果国有大中型企业每年降低采购成本2％-3％,可增加效益500多亿远人民币，相当于1997年国有工业人企业实现利润的总和。因此，采购越来越受到人们的关注和重视，对采购的研究也称为当今社会的热点问题之一。

然而，研究一种高效的智能优化方法来解决物料采购问题非常有意义。企业采购的主要目标是降低企业成本。

K_means算法在大量数据处理中有着非常广泛的应用，它的主要思想是通过迭代过程把数据集划分为不同的类别，使得评价聚类性能的准则函数达到最优，从而使生成的每个聚类内紧凑，类间独立。K_means算法有计算时间短、速度快、容易解释等优点。但是对异常值敏感、对一些问题的解不够精确。

技术实现要素：

针对现有技术的上述不足，本发明要解决的技术问题是提供一种改进的K_MEANS算法对解决制造业物料采购问题。

本发明的目的是克服现有技术中存在的问题：针对制造业采购问题，K_means算法计算精度不够高，对异常值敏感，制造业物料采购问题存在很多折中问题没有解决。

本发明为实现上述目的所采用的技术方案是：一种改进的K_MEANS算法对解决制造业物料采购问题。

该算法的步骤如下：

步骤1：初始化数据集。初始化采购商数据集P，属性(物料)数据集A，采购物料标准X。

步骤2：对供应商数据集进行聚类。用改进的K_Means算法对供应商数据集聚类，把具有相似性较高的供应商聚为一类，具体的为：

(1)确定聚类数量k。

(2)选择聚类中心。随机在供应商集合中选择k个供应商作为初始聚类中心。

(3)计算相异度。用物料种类数量来刻画两个用供应商集合中供应商与聚类中心的距离来表示相异度。

(4)聚类。将每个供应商聚类到与它相异度最小的聚类中心中去。

(5)计算聚类平均值。计算每个聚类中所有供应商的物料种类平均值，并将这个平均值作为新的聚类中心。

(6)反复执行(3)、(4)，直到聚类中心不再进行大范围移动或者聚类次数达到要求为止。

(7)输出聚类。

步骤3：选择最优聚类进行成本考量。最优聚类的选择规则如下：

(1)计算所有类中心到标准采购量的距离。

(2)选择距离最小的聚类作为最优聚类，统计出最优聚类所包含的供应商数量N_best。

(3)成本考量如步骤4所述。

步骤4：计算最优聚类里面每个供应商的成本。

步骤5：计算商家的合适指数。

步骤6：选出适应度最大的物料供应商。

步骤7：计算找出最优成本商家。

步骤8：算法结束，输出最佳结果。

本发明的有益效果是：

1、首先对数据集进行聚类，再对聚类最优集进行属性相似度的考量，较少了算法的计算量，提高算法搜索效率，另一方面，提高了算法解的实用度。

2、以标准购买物料种类数目作为聚类数量，简单有效，减少了算法的复杂度。

3、用物料种类数量来刻画两个用供应商集合中供应商与聚类中心的距离来表示相异度，易于理解，实用性高。

4、选择最优聚类进行成本考量，降低了算法对异常值的敏感程度，同时减小了算法搜寻最优解的范围，同时在最优类内搜寻，得到的解跟理想解会更接近。

5、通过计算最优聚类里面每个供应商的成本，比较，得到最优解。提高的算法解的精确度。

6、通过商家的合适指数，利用成本来刻画供应商的合适指数，使最终解更加可靠。

附图说明

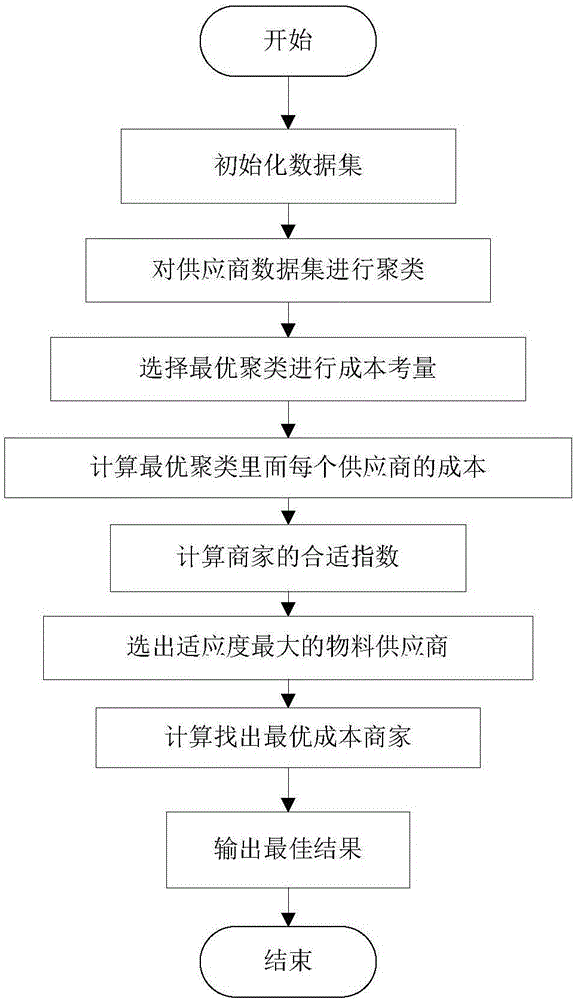
图1为一种改进的K_MEANS算法对解决制造业物料采购问题。

图2为供应商聚类算法图。

具体实施方式

为了使本发明的目的、技术方案及优点更加清楚明白，以下结合算法流程图进行详细、具体说明。

一、物料采购问题的描述

初始化采购商数据集P，属性(物料)数据集A，采购物料标准X。设有K类物资X＝{X_i|i＝1，2，...，K}。分别从供应商资P＝{P_j|i＝1，2，...，N}处采购，每种物资都有采购指标，如价格和运输费用等。在进行采购时，每种物资都选择一个指标作为主要指标，其他指标作为参考指标。如何选择不同物资的供应商，制定一个采购方案X＝{X₁，X₂，...，X_k}，在满足采购量、订货期和资金等约束条件的前提下，使总的采购成本最低。建立规划模型如下：

目标函数：

其中q_i＝f(x₁，x₂，...，x_m)为第i类物资的采购量，q_ix_ij表示第i类物资关于指标j的成本，x_ij表示第j个采购指标值，C(X_i)表示第i类物资的采购成本，C(x^*)为最优采购方案x^*的成本，即最优成本。

约束条件：

1)采购量约束：采购者和供应商对每一项指标都允许有一个浮动的区间，即：x_ij∈[T₁(j)，T₂(j)]，i＝1，2，...，n；j＝1，2，...，m

T₁(j)，T₂(j)分别为指标的下限和上限。

2)资金约束：每类物资的采购资金需满足：

q_i＝f(x₁，x₂，...，x_m)是k次齐次方程，成本函数c(q_i)反映了采购成本与采购量之间的约束关系，l为采购成本。

二、具体实施步骤

步骤1：初始化数据集。初始化采购商数据集P，属性(物料)数据集A，采购物料标准X。P＝{P_j|i＝1，2，...，N}，X＝{X_i|i＝1，2，...，K}，A＝{A_i|i＝1，2，...，N·K}

步骤2：对供应商数据集进行聚类。用改进的K_Means算法对供应商数据集聚类，把具有相似性较高的供应商聚为一类，具体的为：

(1)确定聚类数量k。

(2)选择聚类中心。随机在供应商集合中选择k个供应商作为初始聚类中心。记为V＝{v_c|c＝1，2，...k}。

(3)计算相异度。用物料种类数量来刻画两个用供应商集合中供应商与聚类中心的距离来表示相异度。具体计算为：

其中，n_i为供应商i所能提供的物料种类数目,n_ic为中心点供应商c所能提供的物料种类数目。

(4)聚类。将每个供应商聚类到与它相异度最小的聚类中心中去。

(5)计算聚类平均值。计算每个聚类中所有供应商的物料种类平均值，并将这个平均值作为新的聚类中心。

(6)反复执行(3)、(4)，直到聚类中心不再进行大范围移动或者聚类次数达到要求为止。

(7)输出聚类。

步骤3：选择最优聚类进行成本考量。最优聚类的选择规则如下：

(1)计算所有类中心到标准采购量的距离。计算公式为:

D_c＝|(n_ic-k)|

(2)选择距离最小的聚类作为最优聚类，统计出最优聚类所包含的供应商数量N_best。

(3)成本考量如步骤4所述。

步骤4：计算最优聚类里面每个供应商的成本。

步骤5：计算商家的合适指数。

步骤6：选出适应度最大的物料供应商。选择准则如下：

其中Better对应的供应商记为p。

步骤7：计算找出最优成本商家。计算方法如下:

目标函数：

其中q_i＝f(x₁，x₂，...，x_k)为第i类物资的采购量，q_ix_ij表示第i类物资关于指标j的成本，x_ij表示第j个采购指标值，C(X_i)表示第i类物资的采购成本，C(x^*)为最优采购方案x^*的成本，即最优成本。

约束条件：

1)采购量约束：采购者和供应商对每一项指标都允许有一个浮动的区间，即：x_ij∈[T₁(j)，T₂(j)]，i＝1，2，...，k；j＝1，2，...，N_best

T₁(j)，T₂(j)分别为指标的下限和上限。

2)资金约束：每类物资的采购资金需满足：

q_i＝f(x₁，x₂，...，x_k)是k次齐次方程，成本函数c(q_i)反映了采购成本与采购量之间的约束关系，l为采购成本。

其中最优成本供应商记为q。

步骤8：算法结束，输出最佳结果。