一种改进的自适应多字典学习的图像超分辨率重建方法与流程

本发明属于图像处理技术领域，涉及一种改进的自适应多字典学习的图像超分辨率重建方法，可用于图像的诊断、分析以及进一步的处理。

背景技术：

高分辨率图像包含很多细节信息，这些信息在医学影像、视频监控、遥感成像等领域至关重要，它有利于图像的诊断、分析以及进一步的处理，所以获取高分辨率具有重要意义。若要获得高分辨率图像，有两种途径：一是从硬件方面着手改造成像系统，二是从软件方面通过算法提高图像的分辨率。但是，由于现有芯片与传感器制造工艺、系统成本等方面的限制，从硬件方面提高图像的分辨率很困难，所以从软件方面着手成为提高图像分辨率的重要手段。图像超分辨率(Super-resolution，SR)方法就是利用图像处理技术从一幅或多幅同一场景的低分辨率(Low-resolution，LR)图像中恢复出一幅高分辨率(High-resolution，HR)图像的技术，它将低分辨率成像设备获取图像的过程看作是由HR图像降质得到的，这个问题求解的关键是如何弥补降质过程中丢失的高频信息^[1]。

经典的SR重建方法^[2]是利用同一场景下的多幅图像之间存在的亚像素位移所提供的互补信息来重建HR图像的。这种方法重建效果好，但它受配准精度的影响较大、运作成本高，而且有些领域很难获得同一场景、相近时相下的多幅LR图像。所以基于单幅图像的SR重建方法逐渐发展起来，它主要是利用先验知识或样本学习来获取高频信息的。这其中最简单的是基于插值^[3]的方法，如双线性插值、双立方插值等，这种方法计算简单，运算量低，但重建后图像边缘比较模糊，且存在棋盘和振铃效应。第二种是基于重建的方法，它主要是通过先验知识来获取丢失的高频信息，如凸集投影法^[4]、迭代反投影法^[5]、正则化方法^[6]等，这种方法在一定程度上缓解了插值法的缺点，但当抽取率较大时，重建效果会急剧下降。第三种基于单幅图像的SR重建方法是基于学习的方法^[7，8]，通过学习高、低分辨率图像之间的统计关系，并把这种关系运用到重建过程中来实现图像SR重建，相较于前两种重建方法，基于学习的方法能够获得更多的细节信息，因此重建效果更好。

稀疏表示是在给定的超完备字典中用尽可能少的原子来表示图像，图像经过稀疏表示后可以获得更为简洁的表示方式，从而更容易获取图像中所蕴含的信息，而且图像越稀疏最后重建出的图像精度越高。近几年，稀疏表示模型在基于学习的超分辨率重建算法中取得了较好的效果。Yang等^[9]提出了一种基于稀疏表示的超分辨率算法，该算法从高、低分辨率图像中分别选取图像块作为字典训练样本，利用FSS(Feature-Sign Search)算法训练出一对高、低分辨率字典，然后利用低分辨率字典求出待处理的LR图像的稀疏系数，再利用这个稀疏系数和高分辨率字典重建出HR图像。Zeyde等^[10]在Yang的基础上提出了一种新的基于稀疏表示的超分辨率算法，他提出在字典训练时用K-SVD算法代替Yang的FSS算法，既加快了字典训练速度也提高了重建效果。这两种算法都是利用图像在字典下具有稀疏性这一性质，将这种稀疏性看作正则化项来约束解的唯一性，从而实现图像的SR重建。此外，自然图像中普遍存在大量的重复图案和结构，利用这种局部和非局部的自相似性也可以提高重建效果。例如Glasner等^[11]提出利用图像自相似性产生金字塔，然后在金字塔的不同层搜索相似图像块重建高分辨率图像。Dong等^[12]首先对图像库中的图像块进行聚类，然后对每类样本用主成分分析法训练出多个字典，在重建过程中引入自回归模型和非局部结构自相似性作为正则化项，取得了较好的重建效果。以上方法中，Yang和Zeyde的方法都是仅仅利用图像库来训练字典的，这种通过图像库训练的字典称为全局字典，由于图像库含有丰富的高频信息，所以全局字典能够获取充足的附加信息，但无法保证这些附加信息的准确性和可靠性，因此往往具有较好的视觉效果，却存在较大的均方误差。况且由于图像的多样性，实际上并不存在能够稀疏表示所有图像块的全局字典。Glasner提出的方法利用输入的LR图像自身的自相似性重建图像，这种方法充分利用了自身图像的先验知识，能够保证获取附加信息的准确性和可靠性，但自身图像所蕴含的高频信息是有限的，所以重建效果也存在一定的局限性。Dong的方法虽然利用了自身图像的自相似性信息，增加了获取信息的准确性和可靠性，但其仍然是利用图像库训练全局字典，并不能稀疏表示所有的图像块。此后为了进一步提高重建效果，潘宗序等^[13]将自身图像与图像库相结合提出了一种基于自适应多字典学习方法SR重建算法，他将LR图像进行金字塔分解，对金字塔中的图像块进行聚类，在聚类结果的引导下将图像库中的图像块进行分类，针对各类中的样本构建多个字典，这样每个图像块可根据自身特点自适应的选取适合自己的字典实现SR重建。

本发明在训练字典时，用待处理图像的自相似性生成的金字塔上层图像作为自身样本，以此获得更多的不同尺度下的图像信息；此外，在重建时将金字塔的顶层作为初始重建图像，将稀疏编码的非局部结构自相似性作为正则化约束项来实现图像的超分辨率重建，这样也能利用图像相同尺度下的相似信息来重建图像。实验结果表明，本发明中重建的HR图像无论是在主观评价还是客观评价上都有较好的效果。

本发明能更充分的利用图像相同尺度与不同尺度的相似信息，使重建的图像效果更好、更准确。

参考文献：

[1]潘宗序，禹晶，胡少兴，孙卫东.基于多尺度结构自相似性的单幅图像超分辨率算法[J].自动化学报，2014，40(4)：594-603.Kim S P，Bose N K，and Valenzuela H M.Recursive reconstruction of high resolution image from noisy undersampled multiframes[J].IEEE Transactions on Acoustics，Speech and Signal Processing.1990，38(6)：1013-1027.

[2]Rajan D and Chaudhuri S.Generalized interpolation and its application in super-resolution imaging[J].Image and Vision Computing，2001，19(13)：957-969.

[3]Stark H and Oskoui P.High-resolution image recovery from image-plane arrays，using convex projections[J].Journal of the Optical Society of America A(Optics and Image Science).

[4]Irani M and Peleg S.Motion analysis for image enhancement：resolution，occlusion，and transparency[J].Journal of Visual Communication and Image Representation，1993，4(4)：324-335.

[5]韩玉兵，吴乐南，张冬青.基于正则化处理的超分辨率重建[J].电子与信息学报，2007，29(7)：1713-1716.doi：10.3724/SP.J.1146.2005.01631.

[6]Chang H，Yeung D，and Xiong Y.Super-resolution through neighbor embedding[C].Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition，2004，1：1063-6919.

[7]Freeman W T，Jones T R，and Pasztor E C.Example-based super-resolution[J].IEEE Computer Graphics and Applications，2002，22(2)：56-65.

[8]Yang J，Wright J，Huang T S，and Ma Y.Image super-resolution via sparse representation[J].IEEE Transaction on Image Processing，2010，19(11)：2861-2873.

[9]Zeyde R，Elad M，and Protter M.On single image scale-up using sparse-representation[C].In Proc.of Internation Conferenceon Curves and Surfaces，2010，6920：711-730.

[10]Glasner D，Bagon S，and Irani M.Super-resolution from a single image[C].Proceedings of IEEE Conference on Computer Vision and Pattern Recognition，2009，30(2)：349-356.

[11]Dong W S，Zhang L，Shi G M，and Wu X L.Image deblu rring and super-resolution by adaptive sparse domain selection and adaptive regularization[J].IEEE Transactions on Image Processing，2011，20(7)：1838-1857.

[12]潘宗序，禹晶，肖创柏，孙卫东.基于自适应多字典学习的单幅图像超分辨率算法[J].电子学报，2015，43(2)：209-216.doi：10.3969/j.issn.0372-2112.2015.02.001.

[13]Candès E，Romberg J，and Tao T.Robust uncertainty principles：Exact signal reconstruction from highly incomplete frequency information[J].IEEE Transactions on Information Theory，2006，52(2)：489-509.

[14]Dong W S，Zhang L，Lukac R，and Shi G M.Sparse representation based image interpolation with nonlocal autoregressive modeling[J].IEEE Transactions on Image Processing，2013，22(4)：1382-1394.

[15]Daubechies I，Defrise M，and De Mol C.An iterative thresholding algorithm for linear inverse problems with a sparsity constraint[J].Communications on Pure and Applied Mathematics，2004，57(11)：1413-1457.

[16]Freeman G and Fattal G.Image and Video Upscaling from Local Self-Examples[J].ACM Transactions on Graphics，2011，30(2)：1-11.

[17]Wang Z，Bovik A C，and Sheikh H R，et al.Image quality assessment：from error visibility to structural similarity[J].IEEE Transactions on Image Processing，2004，13(4)：600-612.

[18]http：//www.ifp.illinois.edu/～jyang29/

[19]http：//www.cs.technion.ac.il/～elad/software/.

[20]https：//eng.ucmerced.edu/people/cyang35

[21]http：//see.xidian.edu.cn/faculty/wsdong/wsdong_Publication.htm

技术实现要素：

为了提高图像超分辨率重建效果，综合利用待处理图像自身的信息与自然图像库提供的高频信息，提出一种改进的自适应多字典学习的图像超分辨率重建方法。在训练字典时，用待处理低分辨率图像的自相似性生成的金字塔上层图像作为自身样本代替现有的自适应多字典学习中利用金字塔分解得到的样本，并且在重建的过程中将金字塔的顶层作为初始重建图像，将稀疏编码的非局部结构自相似性作为正则化约束项来实现图像的超分辨率重建。本发明能更充分的利用图像相同尺度与不同尺度的相似信息，使重建的图像效果更好、更准确。实验结果表明，与双三次插值法、Yang算法、Zeyde算法、Glasner算法和Dong算法相比，本发明无论是在视觉效果上还是峰值信噪比和结构自相似性定量指标上都有显著提高。实现本发明目的技术方案，包括下列步骤：

步骤1：根据图像的降质过程确定降采样矩阵D和模糊矩阵B；

步骤2：利用图像自相似性建立金字塔，将金字塔的上层图像和自然图像作为字典学习的样本，用PCA法构建各类的字典并将金字塔的顶层图像作为初始重建图像

步骤3：计算稀疏编码非局部结构自相似的权值矩阵A；

步骤4：设置迭代终止误差e，最大迭代次数Max_Iter、控制非局部正则化项贡献量的常数η以及更新参数的条件P；

步骤5：更新图像的当前估计：

步骤6：更新稀疏表示系数：

其中，soft(·，τ_i，j)为阈值τ_i，j的软阈值函数；

soft(x，τ)＝sgn(x)max(|x|-τ，0)

其中，sgn(x)是符号函数；

步骤7：新图像的当前估计

步骤8：如果mod(k，P)＝0，则更新X的自适应稀疏域，用更新矩阵A；

步骤9：重复(5)～(8)，直到迭代满足或k≥Max_Iter迭代终止。

与现有技术相比，本发明的有益效果是：

1.本发明是对潘宗序提出的算法的改进，在训练字典时，用待处理图像的自相似性生成的金字塔上层图像作为自身样本代替潘宗序提出的自适应多字典学习中利用金字塔分解得到的样本，以此获得更多的不同尺度下的图像信息；此外，在重建时将金字塔的顶层作为初始重建图像，将稀疏编码的非局部结构自相似性作为正则化约束项来实现图像的超分辨率重建，这样也能利用图像相同尺度下的相似信息来重建图像。

2.本发明重建结果更准确，图像边缘更加尖锐，细节更丰富，与其它算法相比，本发明重建出的结果视觉效果最好，恢复了更多的细节，图像更加清晰。

附图说明

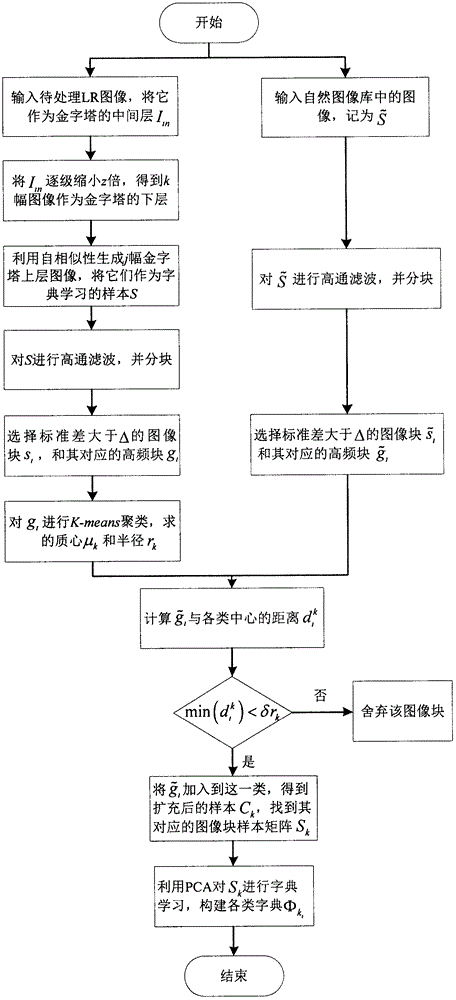
图1：本发明的流程图；

图2：(a)Butterfly原始图像，(b)为Butterfly低分辨率图像，(c)双三次插值算法的重建结果图，(d)Yang算法的重建结果图，(e)Zeyde算法的重建结果图，(f)Glasner算法的重建结果图，(g)Dong算法的重建结果图，(h)为本发明的结果图；

图3：(a)hat原始图像，(b)hat低分辨率图像，(c)双三次插值算法的重建结果图，(d)Yang算法的重建结果图，(e)Zeyde算法的重建结果图，(f)Glasner算法的重建结果图，(g)Dong算法的重建结果图，(h)为本发明的结果图。

具体实施方式

下面结合具体实施方式对本发明作进一步详细地描述。

本发明通过以下步骤实现了基于自适应多字典学习及结构自相似性的图像超分辨率重建方法，具体步骤如下：

步骤1：根据图像的降质过程确定降采样矩阵D和模糊矩阵B；

步骤2：利用图像自相似性建立金字塔，将金字塔的上层图像和自然图像作为字典学习的样本，用PCA法构建各类的字典并将金字塔的顶层图像作为初始重建图像为了得到丢失的高频信息，需要获取包含高频信息的字典。本发明用于字典训练的样本为待处理的图像自身和自然图像库，其中自然图像库主要是选取纹理细节丰富的高分辨率图像，同时利用待处理图像自相似性生成图像金字塔，选取金字塔的上层图像作为字典训练时用于提供图像自身信息的训练样本。利用自相似性生成图像金字塔的原理如下：

将输入低分辨率图像作为中间层I_in，然后将它逐级缩小z倍，得到金字塔的下层图像I_in-1，I_in-2，…，I_in-k(k为缩小的级数)。对于I_in中的图像块M，假设能够在I_in-1和I_in-2中搜索到M的相似图像块P₁和P₂，则可以确定P₁和P₂在I_in中的相应区域Q₁和Q₂，然后将Q₁和Q₂作为图像块M在I_in+1和I_in+2中的相应区域D₁和D₂的估计，根据这一原理逐块计算，从而求得金字塔的上层图像I_in+1，I_in+2，…，I_in+j(j为重建的级数)。如果同一图像块的相似图像块有多个，则可以通过加权计算重建的图像块，即I_in+j中的图像块D_i是由I_in+j-1中M_i的相似图像块P₁～P_m对应的Q₁～Q_m加权得到，公式如下：

D_i＝∑ω_mQ_m

其中，权值

ω_m＝exp(-||M_i-P_m||²/σ²)

式中σ为控制相似度的权值。将所有的D_i叠加就得到了金字塔的上层图像I_in+j。然而并非所有的图像块都能在金字塔中找到它的相似图像块，所以本发明利用反投影算法^[5]来填补这些区域，提高图像的分辨率。自适应多字典的训练原理如下：

首先，对待处理图像进行处理将上面得到的金字塔上层图像作为字典训练的样本S，考虑到人的视觉系统只对高频信息敏感，所以本发明对这些图像进行高通滤波提取它们的高频信息，然后将它们裁剪成大小的图像块，为了保证排除平滑区域，只保留边缘结构，这里只选择图像块标准差大于Δ的图像块。记s_i，i＝1，2，...，m为选择的样本图像块，g_i，i＝1，2，...，m为其对应的高通滤波后的高频成分，通过K-means算法将g_i聚成K类，m_k为每类中包含的样本数，保证计算每类的类中心和类半径

其次，对自然图像库中的图像同样进行高通滤波，然后裁成大小的块，选择图像块标准差大于Δ的块，记为选择的样本图像块，为其对应的高通滤波后的高频成分。计算与上面聚类得到的各类质心μ_k的距离，记为如果则将加入到C_k，否则舍弃该图像块，其中，δ是用来控制图像块与类中心的相似程度的参数。经过上述操作后，样本得到扩充，每类扩充后的样本记为q_k为扩充后样本个数。

然后，根据高频成分样本C_k找到与其对应的图像块样本矩阵k＝1，2，...，K，根据下式进行字典学习，得到K个子字典：

其中，Λ_k为稀疏系数矩阵，λ为控制稀疏程度的参数。为了减少计算量，本发明采用主成分分析法(principal component analysis，PCA)进行字典学习。设S_k的协方差矩阵为Ω_k，对Ω_k进行主成分分析，得到一个正交变换矩阵P_k，假设P_k为字典，则稀疏系数我们期望为了更好的平衡稀疏程度与数据保真项之间的关系，本发明只选择P_k中r个最重要的特征向量组成字典Φ_r＝[p₁，p₂，...，p_r]，则当r减小时，中的重建误差将会增加，||Λ_r||₁的值将会减小。因此，对于K类中的每一类，各自寻找一个最优的r值，记为r₀，用来平衡重建误差与||Λ_r||₁之间的关系，公式如下：

最终求得各类字典

最后，在Φ_k(k＝1，2，...，K)中寻找待重建图像块对应的自适应字典。本发明将利用自相似性生成的金字塔的顶层作为初始重建图像将分为的待重建图像块其对应的高频成分为根据公式求得k_i就可以确定表达图像块的字典

步骤3：计算稀疏编码非局部结构自相似的权值矩阵A；

步骤4：设置迭代终止误差e，最大迭代次数Max_Iter、控制非局部正则化项贡献量的常数η以及更新参数的条件P；

步骤5：更新图像的当前估计：

步骤6：更新稀疏表示系数：

其中，soft(·，τ_i，j)为阈值τ_i，j的软阈值函数；

soft(x，τ)＝sgn(x)max(|x|-τ，0)

其中，sgn(x)是符号函数；

步骤7：新图像的当前估计

步骤8：如果mod(k，P)＝0，则更新X的自适应稀疏域，用更新矩阵A；

步骤9：重复5～8，直到迭代满足或k≥Max_Iter迭代终止。

现结合附图对整个过程做详细介绍：

1.实验中，将原图像作为高分辨率参考图像，然后对它进行模糊、降采样操作生成待重建的低分辨率图像，高斯模糊核尺寸为7×7，标准差为1.6，降采样因子为3。在重建时将待处理的低分辨率彩色图像转换为YCbCr形式，只对亮度分量进行重建，其他两个分量由双三次插值求得。将本发明算法重建结果分别与双三次插值法、Yang算法、Zeyde算法、Glasner算法、Dong算法得到的结果进行比较(后四种算法的程序均可从其相应网站下载[19-22])。实验相关参数设置如下：自然图像库中的样本是从Yang算法样本库中随机选取的20幅图像；建立金字塔时，z＝1.25，k＝4，j＝5；图像块大小n＝36；选取样本时Δ＝4.4；字典中的元素个数为36；相似图像块个数为12；重建时最大迭代次数为999；迭代终止误差为2×10^-6。图2、图3分别为Butterfly和hat这两幅图像的各种算法重建结果图，为了方便比较，将低分辨率图像调成和原始图像同样大小，同时为了更清晰地体现出对比结果，将两幅图像的部分区域进行放大，图2放大了蝴蝶翅膀的纹理，图3放大了帽子上的字母。由图2(c)和图3(c)可以看出，通过双三次插值法重建出的图像较为模糊，边缘比较平滑，视觉效果最差，都不能分辨出帽子上的字母。图2(d)和图3(d)为Yang算法重建出的结果，可以看出重建结果恢复了部分细节，较双三次插值法重建的结果好，但图像仍比较模糊，同样不能分辨出帽子上的字母。图2(e)和图3(e)为Zeyde算法重建结果，可以看出较前两种方法重建结果整体清晰一些，但是蝴蝶翅膀上的纹理依然比较模糊，而且帽子上的字母有伪影，说明Zeyde算法引入了虚假信息。图2(f)和图3(f)为Glasner算法重建结果，整体视觉效果与Zeyde算法相近，但通过局部放大区域可以看出，Glasner算法的重建结果更准确，帽子上的字母不存在伪影，这是因为在重建的过程中它只利用了图像自身进行重建，没有引入外部图像。图2(g)和图3(g)为Dong算法重建结果，可以看出与上面的算法相比，图像边缘更加尖锐，细节更丰富，大体已经能分辨出帽子上的字母。图2(h)和图3(h)为本发明算法重建结果，与其它算法相比，本发明算法重建出的结果视觉效果最好，恢复了更多的细节，图像更加清晰。

2.参数测量结果分析

为了定量证明本发明算法的优势，选取了10幅不同类型的自然图像，它们分别来自于文献[12]、文献[15]和文献[17]，表1列出了各种算法下重建图像的峰值信噪比(PSNR)和结构自相似性(SSIM)[18]的值，其中PSNR值越大说明重建图像越接近原始图像，重建效果越好，SSIM是评价标准高分辨率图像与超分辨率重建图像的结构差异的指标，值越大说明重建效果越好。

通过与双三次插值、Yang算法、Zeyde算法、Glasner算法和Dong算法对比可以得出，相对于这五种算法的重建效果，本发明重建结果的PSNR值分别平均提高4.12dB、3.18dB、1.37dB、3.84dB和0.56dB，SSIM值分别平均提高0.1072、0.0681、0.0169、0.0656和0.0093。这充分说明本发明重建出的图像效果更好。

表1各种算法重建图像PSNR(dB)/SSIM值比较