一种基于指数信号的范德蒙分解的数据补全方法与流程

本发明涉及指数信号的预测与补全，尤其是涉及一种基于指数信号的范德蒙分解的数据补全方法。

背景技术：

在许多实际应用中，如核磁共振波谱和雷达目标定位，我们感兴趣的目标信号可以建模成在频域(相对时域)上若干谱峰的线性叠加，而采集的数据是时域(相对频域)信号，并且符合指数信号。而在实际采样中，通常由于受到硬件、物理条件的限制，实际采样得到的数据并不完整或达不到预期的分辨率，甚至只能得到极少部分的数据。需要补全采集到数据中的丢失部分。或者由于数据量较大，为了加速采样而采用非均匀采样方式，并且需要对采集信号进行数据补全。

比如核磁共振波谱，它在化学分子结构分析领域有着重要的应用，其时域信号符合指数函数。核磁共振实验时间较长，从分钟到几十天不等，这不但使得实验必须耗费大量的谱仪机时，而且加大了实验难度，从而限制了核磁共振技术的应用。为了缩短核磁共振实验时间，一个常见的做法是采用非均匀采样的方式来减少时间域的采样点数(Xiaobo Qu,Xue Cao,Di Guo,Zhong Chen,"Compressed sensing for sparse magnetic resonance spectroscopy,"International Society for Magnetic Resonance in Medicine 18th Scientific Meeting.Stockholm,Sweden,pp.3371,2010.)(Xiaobo Qu,Di Guo,Xue Cao,Shuhui Cai,Zhong Chen,"Reconstruction of self-sparse 2D NMR spectra from undersampled data in indirect dimension,"Sensors,vol.11,no.9,pp.8888-8909,2011.)(Xiaobo Qu,Maxim Mayzel,Jian-Feng Cai,Zhong Chen,Vladislav Orekhov,"Accelerated NMR spectroscopy with low-rank reconstruction,"Angewandte Chemie International Edition,vol.54,no.3,pp.852-854,2015.)，但这样做造成信号的丢失，需要使用信号处理的方法对信号进行补全。

技术实现要素：

本发明的目的在于提供一种基于指数信号的范德蒙分解的数据补全方法。

本发明包括以下步骤：

1)利用范德蒙分解对指数信号的汉克尔矩阵建模；

2)建立一种基于范德蒙分解的指数信号恢复模型；

3)提出基于范德蒙分解的指数信号恢复模型的求解算法；

4)数据后处理：对求解获得的指数信号进行傅立叶变换可得到频谱。

在步骤1)中，所述利用范德蒙分解对指数信号的汉克尔矩阵建模的具体方法可为：一个指数信号x表示为多个指数函数线性叠加的形式：

其中x_j表示指数信号x中的一点，c_r表示指数函数的幅度，R表示指数函数的个数；假设该指数信号x的长度为2N-1，其汉克尔矩阵可以根据范德蒙分解表示成以下形式：

其中矩阵和均为范德蒙矩阵，矩阵表示一个对角矩阵。

在步骤2)中，所述建立一种基于范德蒙分解的指数信号恢复模型测量得到信号y，基于范德蒙分解的指数信号恢复模型为：

其中||·||_*表示求矩阵的核范数，即对矩阵的奇异值求和；||·||₂表示求向量的2范数；表示提取出矩阵第r列，算子和分别表示将向量排列成汉克尔矩阵，并且其汉克尔矩阵分别有m和n行，是非均匀采样算子；y表示测量信号；λ为正则化参数，用于权衡和两项的重要性；是预设的汉克尔矩阵的秩；符号“H”表示矩阵的共轭转置。

在步骤3)中，所述提出基于范德蒙分解的指数信号恢复模型的求解算法的具体方法可为：

为了解决式(13)中的问题，提出松弛模型如下：

其中||·||_F表示对矩阵求弗罗贝尼乌斯范数；β表示正则化参数，与参数λ共同权衡和三项的重要性。

当β趋于无穷大时，式(14)的解将趋近式(13)的解。求解式(14)中的最优化问题，可以采用交替方向乘子法；引入中间变量A_r，B_r和拉格朗日乘子D_r和(参考文献：Xiaobo Qu,Yingkun Hou,Fan Lam,Di Guo,Jianhui Zhong,Zhong Chen,"Magnetic resonance image reconstruction from undersampled measurements using a patch-based nonlocal operator,"Medical Image Analysis,vol.18,no.6,pp.843-856,2014；Xiaobo Qu,Di Guo,Bende Ning,Yingkun Hou,Yulan Lin,Shuhui Cai,Zhong Chen,"Undersampled MRI reconstruction with patch-based directional wavelets,"Magnetic Resonance Imaging,vol.30,no.7,pp.964-977,2012.)。根据以下式(15)-(20)迭代更新变量：

其中符号“*”表示求共轭算子；符号“-1”表示求矩阵的逆；符号“←”表示迭代过程；S_1/β(·)表示奇异值收缩算子(参考文献：J.F.Cai,E.J.Candes,Z.W.Shen,"A singular value thresholding algorithm for matrix completion,"SIAM Journal on Optimization,vol.20,pp.1956-1982,2010.)(Xiaobo Qu,Maxim Mayzel,Jian-Feng Cai,Zhong Chen,Vladislav Orekhov,"Accelerated NMR spectroscopy with low-rank reconstruction,"Angewandte Chemie International Edition,vol.54,no.3,pp.852-854,2015.)；参数β₁，β₂，β和λ是正数。当达到迭代停止准则时，迭代停止；迭代停止准则设定为达到最大迭代次数或x在相邻两次迭代中的误差小于设定的阈值η(取值大于0)。当迭代停止时，可根据式(17)得到完整的指数信号。

在许多实际应用中，由于受到采集设备、物理条件等限制，为了加速采样而只采集部分信号，为了达到预期的分辨率对数据进行填充等原因，需要对采集到的信号进行补全。在信号处理中，指数信号可以用多个指数函数的线性叠加来表示。本发明首先利用范德蒙分解来表示指数信号对应的汉克尔矩阵，并建立一种基于范德蒙分解的信号重建模型，然后通过迭代算法重建信号。这种恢复方法精度高，可以从少量的数据中补全出完整的信号。

本发明的有益效果是：在实际应用中，若目标函数可以建模成指数函数的信号，则可以通过采用本发明提出的一种指数信号补全方法，实现利用少量的数据补全获得完整的信号，从而达到克服采样设备限制，降低采样时间，提高频谱分辨率的目的。

附图说明

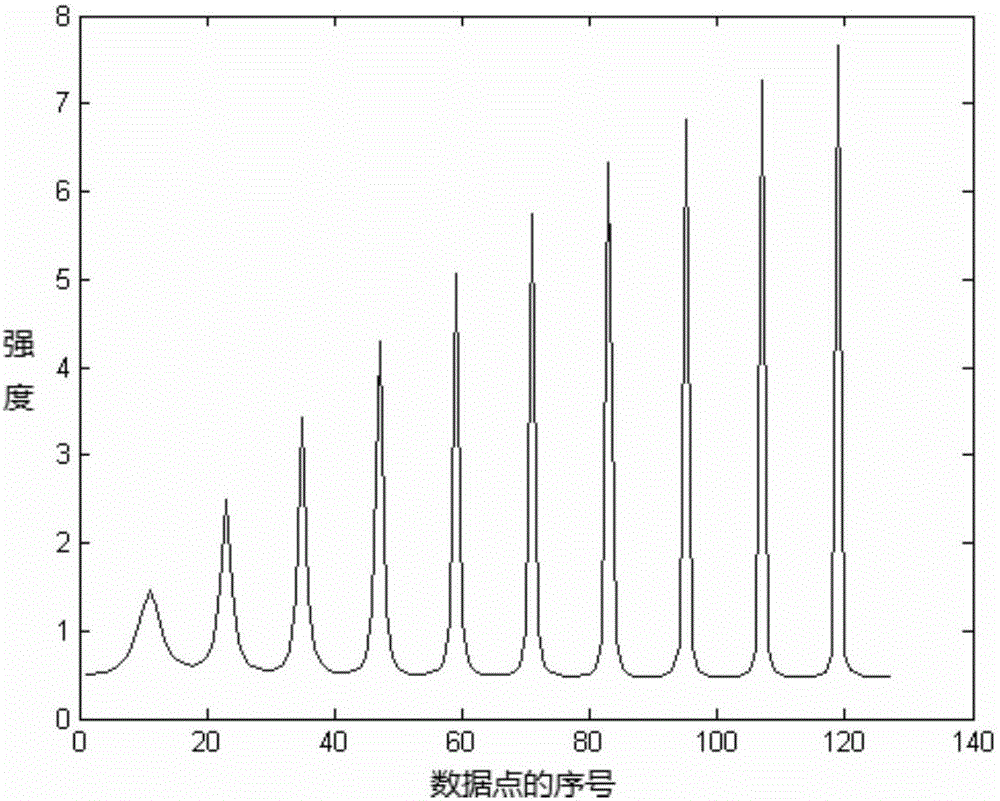
图1为数据补全后所得的一维谱。

图2为数据未丢失的一维谱(作为参考)。

具体实施方式

下面通过具体实施例对本发明作进一步的详细描述，并给出补全的结果。本实施例是一个补全一维指数信号数据的模拟实验。

第一步：确定一个一维指数信号的数据丢失位置

本实施例中，一维指数信号x长度为127，包含了10个谱峰。在模拟数据采集时，一维信号x随机丢失了63个数据，即测量得到的一维指数信号y只含有64个数据。

第二步：构建基于范德蒙分解的指数信号数据补全模型：

其中||·||_*表示求矩阵的核范数，即对矩阵的奇异值求和；||·||₂表示求向量的2范数；表示提取出矩阵第r列，算子和分别表示将向量排列成汉克尔矩阵，并且其汉克尔矩阵分别有m和n行，本实施例中m设为32，n设为64；是非均匀采样算子；y表示测量信号；λ为正则化参数，用于权衡和两项的重要性；是预设的汉克尔矩阵的秩。本实施例中参数设为10。

第三步：提出基于范德蒙分解的指数信号数据补全模型的求解算法：利用以下松弛模型，对(21)求解：

其中||·||_F表示对矩阵求弗罗贝尼乌斯范数；参数β表示正则化参数，与参数λ共同用于权衡和三项的重要性。符号“H”表示矩阵的共轭转置。

采用交替方向乘子法求解公式(22)中的最优化问题。引入中间变量A_r，B_r和拉格朗日乘子D_r和根据以下公式迭代更新变量：

其中符号“*”表示求共轭算子；符号“-1”表示求矩阵的逆；符号“←”表示变量更新；S_1/β(·)表示奇异值收缩算子；参数β₁和β₂设为1，β设为10³，设为10⁵。当达到迭代停止准则时，迭代停止。迭代停止准则设定为达到最大迭代次数10³或x在相邻两次迭代中的误差小于设定的阈值η，η设为10^-6。当迭代停止时，可根据公式(25)得到完整的指数信号。

第四步：数据后处理

对补全的时间信号进行傅立叶变换即可得到谱图(如图1所示)。作为参考，对原始未丢失数据的信号做傅立叶变换得到谱图(如图2所示)。可以看出，利用采集到的部分数据和本发明的数据补全方法，可以重建得到高质量的谱。