一种涡轮叶片热障涂层厚度优化设计方法与流程

本发明属于表面涂层防护技术领域，具体涉及一种涡轮叶片热障涂层厚度优化设计方法。

背景技术：

热障涂层(TBCs)是一种先进的陶瓷金属多层材料系统，在现代涡轮发动机中应用十分广泛。通过在发动机燃烧室、涡轮叶片等高温热端部件表面涂覆具有低热导率的TBCs，一方面可降低金属部件表面温度或进一步提高发动机涡轮叶片燃气入口温度，另一方面可使金属部件免受高温燃气的腐蚀和氧化，从而实现延长热端部件服役寿命和提高发动机效率的目的。以燃气轮机涡轮叶片为例，TBCs和叶片内部冷却的联合作用可有效降低高温合金表面温度100～300℃，使得合金基底能够在高于其熔点温度的环境下长期稳定服役。

TBCs主要由陶瓷层、金属粘接层、高温合金基底、以及在陶瓷层/粘接层界面形成的热生长氧化层构成。TBCs各层材料间存在较大的性能差异，使得制备或高温服役过程中在涂层内部产生显著的热失配应力。较高的热失配应力可能诱发涂层内部裂纹的萌生和扩展，进而导致涂层的剥离失效。因此，应力水平是影响涂层服役寿命的重要因素。TBCs的隔热作用主要依靠表面陶瓷层实现，在给定热流密度的情况下，陶瓷层的热导率和厚度是TBCs隔热性能的两个决定性因素。在选定陶瓷层材料后，TBCs的隔热性能随着陶瓷层厚度的增加而提高，然而涂层内部的应力水平也可能不断升高。对陶瓷层厚度进行设计时，在满足涂层隔热性能的情况下需控制其内部的应力水平，并有必要考虑涂层的制备成本。因此，TBCs结构设计是一个在满足涂层高隔热性能、低应力水平和低制备成本等约束条件下的多目标优化问题。

对涡轮叶片表面涂覆的TBCs进行厚度优化设计，有助于保证涂层服役安全，并提高其性能及使用效率。然而，当前的现有技术只能定性给出涡轮叶片TBCs厚度的大致分布，无法实现准确的厚度分布优化设计，缺少针对TBCs厚度设计优劣的评价。因此，随着表面涂层技术的不断快速发展，在工程应用中迫切需要发展涡轮叶片TBCs的厚度优化设计方法。

技术实现要素：

本发明的目的在于提供一种涡轮叶片热障涂层厚度优化设计方法，该方法能够简单高效的进行优劣的定量评价，有助于保证涂层服役安全和提高涂层使用效率。

本发明是通过以下技术方案来实现：

一种涡轮叶片热障涂层厚度优化设计方法，包括以下步骤：

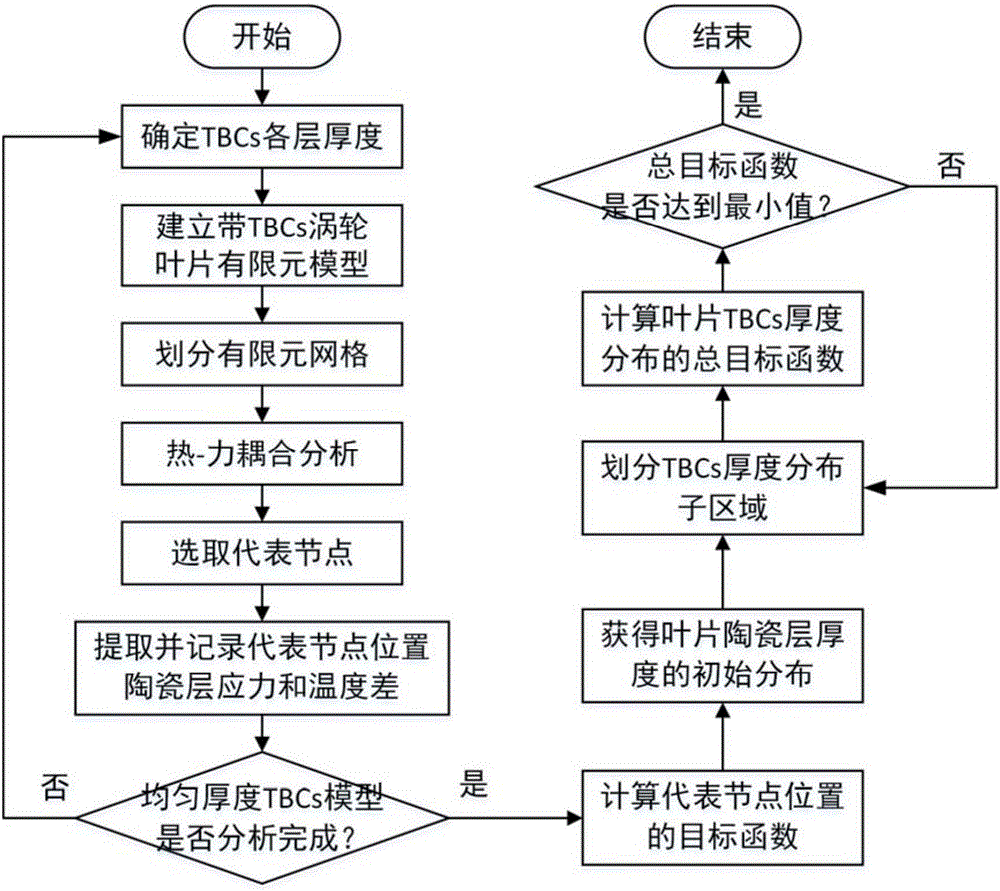
步骤1：确定TBCs各层厚度；

TBCs包含陶瓷层、粘结层及热生长氧化层，为陶瓷层、粘结层及热生长氧化层赋予厚度值；

陶瓷层厚度为k×100μm，k为分析次数的编号，即步骤1至步骤6的重复次数，k＝1,2,…,10；(为了分析不同陶瓷层厚度的结果，步骤1-6需要重复10次，而每次厚度的确定是通过k*100得到的，k就是重复次数)粘接层厚度为100μm～250μm；热生长氧化层厚度为1μm～10μm；

步骤2：建立含TBCs涡轮叶片的三维有限元模型；

三维有限元模型由叶片合金基底和均匀厚度的TBCs构成，TBCs涂覆于涡轮叶片的叶身外表面和叶根平台的上表面；所述均匀厚度TBCs是指涂层覆盖区域内的陶瓷层厚度均相同，TBCs各层厚度由步骤1给定；

步骤3：对三维有限元模型进行网格划分；

步骤4：对划分网格后的三维模型进行热-力耦合分析，获得含TBCs涡轮叶片的整体温度场和应力场分布；

步骤5：选取叶片涂层区域内的代表节点；

代表节点是指能够反映各局部区域的温度和应力状态特征的代表性节点，代表节点位置在不同分析对应的三维有限元模型中一致；

步骤6：提取并记录所有代表节点所在位置的厚度方向，陶瓷层的最大应力值和温度差；

步骤7：判断均匀厚度TBCs模型是否分析完成；

判断k≤10是否成立，若成立则重复步骤1至步骤6；否则，按照步骤8进行；

步骤8：对步骤5中选定的任意代表节点i，i＝1,2,…,110，根据公式(1)分别计算第k次分析对应的有限元模型中该代表节点位置的目标函数值：

公式(1)中，是第k次分析中代表节点i位置处的目标函数，是第k次分析中代表节点i位置处陶瓷层内最大应力，是第k次分析中代表节点i位置处陶瓷层内的温度差，是第k次分析中代表节点i位置处陶瓷层的厚度，w_β是性能权重系数，取w_β＝0.6；w_h是厚度权重系数，取w_h＝0.4；

步骤9：获得叶片陶瓷层厚度的理想分布，对于任意代表节点，求得使其目标函数值最小时的最佳陶瓷层厚度；

步骤10：根据步骤9中获得的叶片陶瓷层厚度理想分布，划分TBCs厚度分布子区域，子区域的陶瓷层厚度与其包含的代表节点中最佳陶瓷层厚度的最大值相同；

步骤11：计算叶片TBCs厚度分布的总目标函数；根据步骤10中给出的子区域陶瓷层厚度分布，并结合公式(1)计算得到的目标函数值，按照公式(2)计算叶片TBCs厚度分布的总目标函数值：

公式(2)中，G_obj是当前TBCs厚度分布的总目标函数值，g_i是代表节点i位置处的目标函数；

步骤12：确定TBCs厚度分布方案；

重复步骤10和步骤11，不断调整子区域大小，直至公式(2)计算获得的G_obj最小，获得涡轮叶片TBCs厚度分布的优化设计方案。

步骤4中，所述热-力耦合分析是通过有限元软件ABAQUS完成，该过程包括以下步骤：

a.对所述三维有限元模型中的合金基底和TBCs分别赋予材料属性；

b.对所述三维有限元模型中的TBCs外表面施加高温边界条件，对叶片冷却通道表面施加冷却温度边界条件；

c.利用ABAQUS提供的热-力耦合分析模块，对有限元模型进行分析计算；

d.计算完成后，在ABAQUS后处理模块输出计算结果，获得含TBCs涡轮叶片的整体温度场和应力场分布。

步骤5中，代表节点针对所述三维有限元模型，在ABAQUS后处理模块中，从叶身吸面选取均匀分布的50个代表节点，从叶身压面选取均匀分布的50个代表节点，从叶根平台选取均匀分布的10个代表节点。

步骤6所述厚度方向指叶片表面的法线方向；所述温度差是指陶瓷层外表面与陶瓷层/热生长氧化层界面之间的温度差值。

步骤9中，所述最佳陶瓷层厚度指在此代表节点区域涂覆该厚度的陶瓷层时，获得隔热性能、应力水平和制备成本之间的最佳协调；根据所有代表节点区域的最佳陶瓷层厚度结果，获得叶片陶瓷层厚度的理想分布。

步骤10中，划分TBCs厚度分布子区域，是将叶身压面分为3个子区域，叶身吸面分为3个子区域，叶根平台分为1个子区域；所述叶身压面和吸面的子区域沿叶片高度方向划分，每个子区域内包含多个代表节点。

与现有技术相比，本发明具有以下有益的技术效果：

本发明公开的涡轮叶片热障涂层厚度优化设计方法，通过在涡轮叶片上选取均匀分布的代表节点，以代表节点位置的温度和应力结果来反映各局部区域的状态，将复杂叶片的TBCs厚度分析等效为对有限数量的代表节点位置的厚度优化设计，大大减少了分析计算量；将复杂的叶片TBCs厚度设计定义为明确的多目标优化问题，建立数学公式来反映高隔热性能、低应力水平和低制备成本的设计目标，通过引入多目标优化算法计算得到每个代表节点位置的最佳陶瓷层厚度，将总目标函数值作为叶片TBCs厚度的优化设计和评价参数，从而能够定量评价TBCs厚度分布方案的优劣，克服现有方法仅能定性评价的缺点。因此，本发明的涡轮叶片热障涂层厚度优化设计方法，可以简单高效的进行TBCs厚度优化设计，并能实现设计方案优劣的定量评价，有助于保证涂层服役安全和提高涂层使用效率。

附图说明

图1是燃气轮机涡轮叶片热障涂层厚度优化设计方法流程图；

图2是燃气轮机涡轮叶片模型图；

图3是叶身压面代表节点分布及厚度子区域划分；

图4是叶身吸面代表节点分布及厚度子区域划分；

图5是叶根平台代表节点分布；

图6是叶身陶瓷层厚度分布结果。

图中，1-叶身压面，2-叶身吸面，3-叶根平台，4-陶瓷层，5-热生长氧化层，6-金属粘接层，7-高温合金基底，8-代表节点，9-叶身压面子区域1，10-叶身压面子区域2，11-叶身压面子区域3，12-叶身吸面子区域1，13-叶身吸面子区域2，14-叶身吸面子区域3，15-叶片冷却通道。

具体实施方式

下面结合具体的实施例对本发明做进一步的详细说明，所述是对本发明的解释而不是限定。

本发明的优化设计流程如图1所示，为了更好的理解本发明的技术方案，将以上优化设计方法应用于燃气轮机涡轮叶片的TBCs厚度设计，涡轮叶片如图2所示。

本实施例的具体过程包括以下步骤：

步骤1：确定TBCs各层厚度。

所述TBCs包含陶瓷层、粘接层和热生长氧化层。选定陶瓷层厚度为k×100μm，其中k为分析次数的编号，即步骤1至步骤6的重复次数，k＝1,2,…,10。本实施例选定的粘接层厚度为150μm，选定热生长氧化层厚度为5μm。

步骤2：建立含TBCs涡轮叶片的有限元模型。

采用有限元软件ABAQUS建立含TBCs涡轮叶片的三维有限元模型。所述有限元模型由叶片合金基底和均匀厚度的TBCs构成，TBCs涂覆于涡轮叶片的叶身外表面和叶根平台的上表面；所述均匀厚度TBCs是指涂层覆盖区域内的陶瓷层厚度均相同，TBCs各层厚度由步骤1给定。

步骤3：对所述有限元模型划分网格。

采用ABAQUS对有限元模型划分网格。对于叶身和平台的合金基底，划分名义尺寸为1mm的六面体网格，单元类型为六面体单元C3D8R；合金基底的其余部分划分名义尺寸为2mm的四面体网格，单元类型为四面体单元C3D4。叶片的陶瓷层在厚度方向划分为5层六面体单元，热生长氧化层在厚度方向划分1层六面体单元，粘接层在厚度方向划分2层六面体单元；所述厚度方向指叶片表面的法线方向。

步骤4：采用ABAQUS对所述有限元模型进行热-力耦合分析，分析过程包括：

a.对所述有限元模型中的合金基底赋予材料属性，本实施例中合金基底的弹性模量为220GPa，泊松比0.31，热膨胀系数12.6×10^-6/℃^-1，热导率11.5W/m℃；

b.对所述有限元模型中的陶瓷层赋予材料属性，本实施例中陶瓷层的弹性模量为48GPa，泊松比0.1，热膨胀系数9×10^-6/℃^-1，热导率1.2W/m℃；

c.对所述有限元模型中的热生长氧化层赋予材料属性，本实施例中热生长氧化层的弹性模量为400GPa，泊松比0.23，热膨胀系数8×10^-6/℃^-1，热导率10W/m℃；

d.对所述有限元模型中的粘接层赋予材料属性，本实施例中粘接层的弹性模量为200GPa，泊松比0.3，热膨胀系数13.6×10^-6/℃^-1，热导率5.8W/m℃；

e.对所述有限元模型中的TBCs外表面施加1150℃的温度边界条件，对叶片冷却通道表面施加700℃的温度边界条件；

f.对有限元模型进行热-力耦合分析计算；

g.计算完成后，在ABAQUS后处理模块输出计算结果，获得有限元模型的整体温度场和应力场分布。

步骤5：选取叶片涂层区域内的代表节点。

所述代表节点是指可反映局部区域的温度和应力状态特征的代表性节点。在ABAQUS后处理模块中，从叶身压面选取图3所示的50个均匀分布代表节点，从叶身吸面选取图4所示的50个均匀分布代表节点，从叶根平台选取图5所示的10个均匀分布代表节点。所述代表节点位置在不同分析对应的有限元模型中一致。

步骤6：提取并记录所有代表节点所在位置处，陶瓷层在厚度方向的最大应力值和温度差。

在ABAQUS后处理模块中，提取并记录所有代表节点所在位置处，陶瓷层在厚度方向的最大应力值和温度差。所述厚度方向指叶片表面的法线方向。所述温度差是指代表节点所在位置处，陶瓷层外表面与陶瓷层/热生长氧化层界面之间的温度差值。

步骤7：判断k≤10是否成立，若成立则重复步骤1至步骤6，否则按照步骤8进行。本实施例共需分析10种不同均匀陶瓷层厚度的叶片模型，用k表示分析次数的编号，也即步骤1至步骤6的重复次数，其中k＝1,2,…,10。

步骤8：对步骤5中选定的任意代表节点i(i＝1,2,…,110)，根据公式(1)分别计算第k次分析对应的有限元模型中该代表节点位置的目标函数值：

公式(1)中，是第k次分析中代表节点i位置处的目标函数，是第k次分析中代表节点i位置处陶瓷层内应力的最大，是第k次分析中代表节点i位置处陶瓷层的温度差，是第k次分析中代表节点i位置处陶瓷层的厚度；w_β是性能权重系数，取w_β＝0.6；w_h是厚度权重系数，取w_h＝0.4。

步骤9：获得叶片陶瓷层厚度的理想分布。

对于任意代表节点i，求得使其目标函数值达到最小时的陶瓷层厚度是代表节点i位置处的最佳陶瓷层厚度。所述最佳陶瓷层厚度指在此代表节点区域涂覆该厚度的陶瓷层时，可获得隔热性能、应力水平和制备成本之间的最佳协调。根据所有代表节点区域的最佳陶瓷层厚度结果，获得叶片陶瓷层厚度的理想分布。

步骤10：划分TBCs厚度分布子区域。

根据步骤9中获得的叶片陶瓷层厚度理想分布，并结合制备工艺的可实现性，将叶身压面分为3个子区域，叶身吸面分为3个子区域，叶根平台分为1个子区域。所述叶身压面和吸面的子区域沿叶片高度方向划分，如图3和图4示意。所述子区域包含多个代表节点，这些代表节点的最佳陶瓷层厚度不尽相同；为此，对于任意给定的子区域，子区域内具有相同的陶瓷层厚度，指定陶瓷层厚度与其包含的代表节点中最佳陶瓷层厚度的最大值相同。

步骤11：计算叶片TBCs厚度分布的总目标函数。

根据步骤10中给出的子区域陶瓷层厚度分布，并结合公式(1)计算得到的目标函数值，按照公式(2)计算叶片TBCs厚度分布的总目标函数值：

公式(2)中，G_obj是当前TBCs厚度分布的总目标函数值，g_i是代表节点i位置处的目标函数。

步骤12：确定TBCs厚度分布方案。

重复步骤10和步骤11，不断调整子区域大小，直至公式(2)计算获得的G_obj最小，以此获得涡轮叶片TBCs厚度分布的优化设计方案。

本实施例优化设计得到的叶身陶瓷层厚度分布如图6所示，根据该厚度方案计算得到总目标函数值G_obj＝54.91；而均匀厚度分布方案中，陶瓷层厚度为400μm时G_obj＝70.25，优化设计方案的总目标函数值比均匀厚度方案降低了27.9％。由此可见，本发明的涡轮叶片热障涂层厚度优化设计方法能够明显提高涂层使用效率，并提高涂层服役性能且降低制备成本。