基于模拟退火蚁群算法的路径规划的制作方法

本发明属于路径规划技术领域，涉及一种基于模拟退火蚁群算法的路规划方法，在传统的蚁群算法的基础上引进了模拟退火算法形成模拟退火蚁群算法，再将其运用于路径规划，为进一步确保找到最优路径避免局部最优，本发明中又加入了增熵策略，通过多次更新路径，避免算法早熟，更易找到全局最优解。最后，经过仿真，也证明了此算法的高效性。

背景技术：

在有障碍物的环境中，搜寻者(如机器人，无人机等)从出发点到目标点规划出一条路径，并能够沿着该路径在没有人为干预的情况下移动到预设目标，并完成预定任务。通常依据对环境信息掌握的程度将路径规划分为2种：

1.环境信息完全已知的全局路径规划——全局路径规划的任务是根据先验(已知)地理环境信息找出从起始位置到目标位置的符合一定需求的可行或最优路径。常用方法有：可视图法，栅格法，自由空间法等。

2.环境信息不完全已知或未知的基于传感器的局部路径规划——局部路径规划是指搜寻者在运行过程中，通过自身安装的传感器不断感知探索周围环境信息，对路径进行实时调整后寻找到一条最优路径。常用方法有：人工势场法，模糊逻辑算法，神经网络算法，遗传算法，蚁群算法等。

我国是一个产煤大国，绝大多数煤矿地形复杂，环境恶劣，煤矿开采的过程中有诸多不安全(例如塌方、透水、瓦斯爆炸等)因素存在，灾难时有发生，矿井发生灾害时，矿工需要在随身携带的定位导航装置的引导下快速逃生，应急救援过程中，救护队员、矿用无人机或机器人的导航是保障救援的基础，因此进行煤矿井下导航路径规划具有重要的理论和实用价值，煤矿矿井巷道狭长密闭、随着开采过程不断变化，在灾害发生时和后续的救援过程中，矿工的目标终点和救护队员的相反的，由于巷道中存在有毒有害气体和巷道的地形结构，矿工和救护队员与机器人和无人机的在井下可行路径是不同的，机器人和无人机在井下的可行路径也不同，深入研究在煤矿井下复杂环境不同参数条件下的路径规划对保障煤矿安全生产和提高应急救援技术水平具有重要的意义。

技术实现要素：

本发明的目的在于针对传统的蚁群算法因为早熟而产生产生局部最优路径问题，为了解决这一问题，提出模拟退火算法与蚁群算法结合的算法，提高了收敛速度,为了进一步确保找到最优路径，又加入了增熵策略，避免算法早熟，增加迭代次数，从而找到全局最优解。

为了更清晰的阐述本发明的方法，先对蚁群算法做适当说明。

蚁群算法(Ant Colony Algorithm,)是意大利学者Dorigo M等人于90年代创立的，是一种用来在图中搜索优化路径的机率型算法，最初是用于解决著名的旅行商问题。它是一种收到自然界真实蚁群启发的搜索算法。蚂蚁是一种群居昆虫，他们有组织，有分工，还有通讯系统，他们相互协作，能完成从蚁穴到食物源寻找最短路径的复杂任务。模拟蚂蚁群体智能的人工蚁群算法的特点是分布计算、信息正反馈和启发式搜索，且易于与其他算法结合因此被广泛地应用到有约束的优化问题中。

用传统蚁群算法解决路径规划问题，依据蚂蚁在觅食过程中会在走过的路径上留下信息素，所走的路径越短，留下的信息素就越多，蚂蚁就越倾向于选择该路径，所以最优路径上的信息素会越来越多，这样形成一个正反馈机制，促使整个群体找到最优路径。首先设m是蚁群中蚂蚁的总数目为m,一个节点i和另一节点j之间的距离用d_ij表示，蚁群算法的迭代次数为N_c，τ_ij(t)表示t时刻结点i、j连线上残留的的信息量。初始时刻t＝0时，将m只蚂蚁放置到起始位置上，令各条路径上的信息素量相等，设τ_ij(0)为常数，蚂蚁k(k＝1,2,3,…m)在运动过程中根据各条路径上的信息素量决定转移方向，将当前走过的节点记录在禁忌表(tabu list)中，禁忌表中的集合tabu_k随着蚂蚁不断前进而动态调整。在搜索过程中，蚂蚁的状态转移概率是根据各条路径上的信息素浓度及路径的启发信息来计算的。在t时刻，蚂蚁k选择从结点i到结点j的转移概率为：

其中，allowed_k＝{C-tabu_k}表示蚂蚁k下一步允许选择的结点，allowed_k为空集时表示蚂蚁完成了一次循环。α(0＜α＜1)为信息启发式因子，它的值越大则蚂蚁之间的协作性越强，蚂蚁越倾向于选择其他蚂蚁所经过的路径；β(0＜β＜1)为期望启发式因子，它的值越大，则该状态转移概率越接近于贪心规则；η_ij(t)为启发函数，其表达式如下：

η_ij(t)＝1/d_ij (2)

式中,d_ij是相邻两结点i和j之间的距离。可以看出，d_ij越小，则η_ij(t)越大，也就越大，该启发函数表示蚂蚁从结点i转移到结点j的期望程度。为了避免残留信息素过多而淹没

启发信息，当每只蚂蚁从起始点到达目标节点(也即一个循环结束)后，要对残留信息进行更新处理。更新规则如下：

τ_ij(t+n)＝(1-ρ)·τ_ij(t)+Δτ_ij(t) (3)

其中，0≤ρ＜1，表示信息素挥发系数，(1-ρ)表示信息残留因子，Δτ_ij(t)表示本次循环路径(i,j)的信息素的增量，初始时刻Δτ_ij(0)＝0，表示第k只蚂蚁在本次循环中留在路径(i,j)上的信息量，Q表示信息素浓度，L_k表示第k只蚂蚁在本次循环中所走路径的总长度。

基于蚁群算法的路径规划流程图如附图1所示。

模拟退火算法是在本世纪80年代初被提出的,想法来源于固体退火原理,将固体加热至充分高，再让其徐徐冷却,加热时,固体内部粒子随温升变为无序状,内能增大,而徐徐冷却时粒子渐趋有序,在每个温度都达到平衡态,最后在常温时达到基态,内能减为最小。根据Metropolis准则,粒子在温度T时趋于平衡的概率为e^-ΔE/(KT),其中E为温度T时的内能,ΔE为其改变量,K为玻尔兹曼常数。在蚁群算法中加入模拟退火算法，将内能模拟为目标路径，将温度演化成一个控制函数Tc，由初始解和控制函数数初始值t0开始，对蚁群算法所得路径重复“产生新路径，计算目标路径差，接受或舍弃”的更新操作，并逐步衰减Tc的值。

将模拟退火算法与蚁群算法结合需设定随着时刻t而变化的控制函数Tc的值，Tc的值可根据需要改变大小来保证整个迭代过程的顺利进行。将模拟退火蚁群算法运用于路径规划具体步骤为：系统控制函数为Tc,初始值记为T_c(0)＝0，t时刻T_c(t)＝T_t，将m个蚂蚁放在起点处，每个蚂蚁按照(1)式进行下一步转移，转移过程中根据传感器实时探测周围的环境而避开障碍物，将其所走过的节点加入禁忌表，直到到达终点。当m个蚂蚁都到达终点时，完成一轮搜索，这一过程可称为寻优过程，在这一过程中Tc的值成线性增长。完成一轮寻优之后取得的路径解集称为初始解集{u_k(c_k,l_k)1≤k≤m}，式中u_k(c_k,l_k)是蚂蚁k取得的解，c_k是经过的路径；l_k是路径长度。u_{l_min}(c_{l_min},l_{l_min})表示初始集中的最优的蚂蚁个体取得的解，其中,c_{l_min}和l_l-min分别初始集中最优路径即局部最优路径的节点路径和长度。加入模拟退火算

法后由初始集生成更新集，更新集记作{u_k′(c_k,l_k)|1≤k≤m}，根据(6)、(7)式逐一计算初始集内的各个蚂蚁的解，决定初始集内的解是否加入更新集，即：

Δl＝l_k-l_l-min； (6)

若p_t＝1,则u_k(c_k,l_k)被接受作为更新集{u_k′(c_k,l_k)}内的解；否则产生一个[0,1]区间的均匀分布的随机数ξ,若p_t＞ξ,则u_k进入更新集,否则u_l-min进入更新集.对所有初始集内的个体进行筛选形成更新集{u_k′(c_k,l_k)|1≤k≤m}。然后按照(8)、(9)式对路径上的信息素进行更新，

τ_i,j(t+1)＝max{τ_i,j(t+1)′,τ_min} (9)

式中:τ_i,j′(t+1)表示更新后更新集中最优路径在节点(i,j)上的信息素，τ_i,j(t+1)为更新后当前最优路径在节点(i,j)上的信息素，r为常数,在每一轮信息素更新时,按照设定的比例加强当前最优路径上的信息素；ρ为信息素挥发系数；是更新集内个体u_k′在路径(i，j)上留下的信息素强度,

Δτ_min是当前优路径在节点(i,j)上留下的信息素强度,

Q为设定的常数。

从更新路径到更新信息素的这一阶段可称为更新过程，这一过程中控制函数按照公式(12)衰减，

T_c(t+1)＝T_c(t)a (12)

式中a为控制系数，且0＜a＜1。由公式(7)可看出，当Tc较大时，初始集中的较差路径能以较高的概率被接受进入更新集中，此时各条路径上的信息素分布更广。随着Tc减小，概率变小，信息素趋于集中分布，算法得以快速收敛，为了使算法更快的收敛，可使a取较小值，这样可以使Tc更快衰减，更快找到更优解。完成一轮更新后得到一条最优路径，这一过程可视为在Tc衰减过程中达到基态。

为了进一步确保找到最优路径，本发明采用增熵策略，即给Tc设置一个[T_max,T_min]的范围，当T_c＜T_min时，Tc自动上升至T_max，重新进行路径更新，这一过程称为增熵过程。本发明中设定了多次增熵,也就是通过多次更新路径来避免局部最优路径，增熵次数记为H,最大增熵次数记为H_max，H_max次增熵后一轮迭代结束[9]，然后进行下一轮迭代，最终计算出最优路径。

基于模拟退火蚁群算法的路径规划可参见附图2。

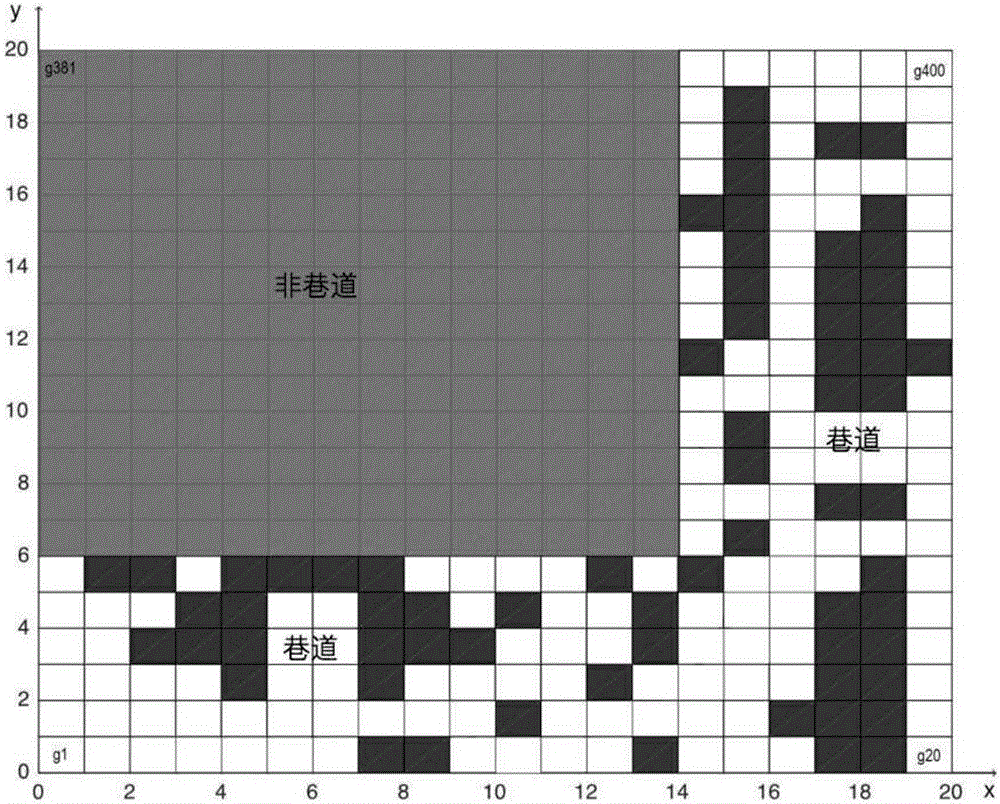
本发明模拟煤矿井下寻优时将蚂蚁演变为搜寻者，利用栅格法建立环境模型来模拟发生矿难后煤矿井下的工作环境，井壁或顶板坍塌后散落在矿井中成为搜索者行进路径上的障碍物[10]，下图模拟矿井中某一段区域的地形，首先以O为坐标原点，水平向右为x轴正方向，竖直向上为y轴正方向，建立直角坐标系，以搜寻者的步长δ为单位，建立一个20*20的栅格环境。其中灰色区域不属于巷道中的区域，在巷道中随机配置障碍物，若某一栅格内没有障碍物，则此栅格为自由栅格，用白色表示，若该栅格内有障碍物，则为障碍栅格，用黑色表示。为了便于标记，在栅格左下方按从左到右，从下到上的顺序为每个栅格编号，序号为从g1到g400。设路径规划的起始位置g₁为搜寻者的起始点,目标位置g400为目标点。环境模型如附图3所示。由仿真得出基于蚁群算法的路径规划用时10.065334seconds，最优路径长度39.8980，而基于模拟退火蚁群算法的路径规划用时9.093760seconds，最优路径长度为39.3120。由附图4和附图5，及两种算法最终得出的最优路径长度可以看出，蚁群算法陷入了局部最优路径，而模拟退火蚁群算法则避免了局部最优路径，通过模拟退火找到了最优路径，且基于模拟退火蚁群算法的路径规与基于蚁群算法的路径规划相比节省了时间。比较以上附图6和附图7，可以得出，模拟退火蚁群算法通过增加迭代次数以寻找最优路径，避免因蚁群算法早熟而形成局部最优路径。

本发明的有益效果是：

1.本发明提出的模拟退火蚁群算法将蚁群算法与模拟退火算法相结合既适用于环境信息已知的情况，又适用于环境信息未知的情况。

2.避免了传统蚁群算法蚁群算法过早成熟而带来的局部最优值问题，且算法更高效，提高了寻优速度，仿真结果表明模拟退火蚁群算法的优越性。

附图说明

图1是本发明所涉及的基于蚁群算法的路径规划的流程图。

图2是本发明所涉及的基于模拟退火蚁群算法的路径规划的流程图。

图3是本发明的仿真模拟环境。

图4是本发明的仿真结果：基于蚁群算法的路径规划的仿真所得出的最优路径。

图5是本发明的仿真结果：基于模拟退火蚁群算法的路径规划的仿真所得出的最优路径。

图6是本发明的仿真结果：蚁群算法的收敛曲线。

图7是本发明的仿真结果：模拟退火蚁群算法的收敛曲线。