一种基于概率图的变压器状态关联规则挖掘方法与流程

本发明属于高压电力设备绝缘监测技术领域，尤其涉及一种基于概率图的变压器状态关联规则挖掘方法。

背景技术：

电力变压器是电网运行的基础单元，对变压器状态进行全面、准确的评价、诊断和预测，是状态检修和全寿命周期管理的前提条件，也是智能调度运行的重要依据，可以为电网安全、可靠、高效运行提供有力的技术支撑。

现有变压器状态评价和诊断模型主要基于单一或少数状态参量进行分析和判断，多数局限于阈值诊断的范畴，无法充分利用设备大量状态信与电网运行和环境气象之间蕴含的内在规律和关联关系进行综合分析，状态评价结果片面，同时也无法全面反映故障演变与表现特征之间的客观规律，难以实现其潜伏性故障的发现和预测。因此对变压器状态信息，结合电网运行信息及气象信息数据进行关联规则挖掘将有助于提高设备状态预测的精度，从而有助于设备潜在性故障的发现和诊断。

目前常用的关联规则挖掘算法主要有三种经典算法，即Apriori算法、AprioriTid算法及AprioriHybrid算法。其中，Apriori算法每次循环都要扫描一遍数据库，用来计算候选项集的支持度。随着项集阶数的增加，候选项集的个数逐渐减少，但是每次循环扫描的数据量并没有变；AprioriTid算法使用逐渐减少的事务标识表代替原始数据库，减少了搜索量，但是在循环初始阶段，候选项集的个数往往大于数据项个数。AprioriHybrid算法总体性能优于Apriori算法和AprioriTid算法，但当转换出现的便利是最后一次时，AprioriHybrid算法比AprioriTid算法差，且算法复杂。

传统的动态贝叶斯网络模型通过建模相邻的连续时间段上的条件依赖关系实现对未来状态的预测。由于变压器运行环境的动态性，导致相邻时间段系统参数的变化不存在明显的因果关系，而连续时间段上系统参数的波动规律却能反映一类特定的事件，例如气象变化或设备出现故障。因此将多个系统参数之间的关联规则引入可以显著提高状态预测和故障诊断的精确度。

技术实现要素：

本发明的目的就是为了解决上述问题，提出了一种基于概率图的变压器状态关联规则挖掘方法，该方法利用概率图分析关联规则，避免了搜索各阶频繁项集都需要循环扫描所有数据项，提高了关联规则挖掘的效率，利用该关联规则可以使状态预测更加精确。

为实现上述目的，本发明的具体方案如下：

一种基于概率图的变压器状态关联规则挖掘方法，包括以下步骤：

(1)从数据库中读取设定变压器状态量数据；构建变压器状态量关联规则挖掘的数据集；

(2)利用Apriori算法，找出变压器状态量数据集中所有的频繁2-项集；

(3)筛选频繁2-项集，并计算筛选后的所有频繁2-项集之间的条件概率分布；

(4)根据筛选后的频繁2-项集，以频繁2-项集及不同频繁2-项集之间的条件概率分布为边，构造概率图；

(5)根据所述概率图，找出所有的关联规则，生成关联规则集合；

(6)计算每一条关联规则的支持度和置信度，根据计算得到的支持度和置信度确定变压器各状态量之间的关联程度；将各状态量数据间的关联规则引入变压器状态预测，对预测结果进行修正。

进一步地，所述步骤(1)中，变压器状态量关联规则挖掘的数据集中包含的数据包括：变压器油色谱数据、油温数据以及变电站气象数据。

进一步地，所述步骤(2)的具体方法为：

1)将变压器状态量数据集记为D，D＝{t₁,t₂,L,t_n}，其中t_k＝{i₁,i₂,L,i_p}，则将t_k(k＝1,2,L,n)称为事务，i_m(m＝1,2,…,p)称为项；

2)扫描变压器状态量数据集中的所有事务，计算每项出现的次数，产生频繁1-项集L₁；

3)根据频繁1-项集L₁得到频繁2-项集L₂。

进一步地，所述步骤3)的具体方法为：

Step1：连接和剪枝：对每两个有1个共同项目的频繁1-项集L₁进行连接得到C'₂，并根据频繁项集的反单调性，对C'₂进行剪枝，得到候选2-项集C₂；

Step2：扫描变压器状态量数据集，确定每个事务t所含候选2-项集C₂的支持度subset(C₂,t),并存放在hash表中；

Step3：设定最小支持度阈值minSup，删除支持度低于minSup的项集，得到频繁2-项集L2。

进一步地，所述步骤(3)中，筛选频繁2-项集的方法具体为：

求取筛选频繁2-项集X与Y的P-S兴趣度interest(X,Y)；若interest(X,Y)≈0，那么X和Y相互独立，将关联规则从频繁2-项集中删除；

进一步地，所述求取筛选频繁2-项集X与Y的P-S兴趣度interest(X,Y)的方法为：

其中，support(X)、support(Y)分别指项集X、Y的支持度；support(XUY)指的是项集XUY的支持度；

进一步地，所述步骤(6)中，计算关联规则的支持度的方法为：

其中，σ_XUY为项集XUY的支持数，即变压器状态量数据集D中包含项集XUY的事务数；|D|是变压器状态量数据集D中的元素个数。

进一步地，所述步骤(6)中，计算关联规则的置信度的方法为：

其中，support(X)、support(XUY)分别指的是项集X、XUY的支持度。

进一步地，所述步骤(6)中，设定设定最小支持度阈值minSup和最小置信度阈值minConf；

若关联规则满足且称关联规则为强关联规则，否则称关联规则为弱关联规则；

其中，为关联规则的支持度，为关联规则的置信度。

本发明的有益效果：

本发明方法利用概率图分析关联规则，避免了搜索各阶频繁项集都需要循环扫描所有数据项。仿真结果表明，将经过数据挖掘得到的数据间关联规则引入状态预测对预测结果进行修正可以显著提高预测精度：平均预测误差从20％下降到了10％。

附图说明

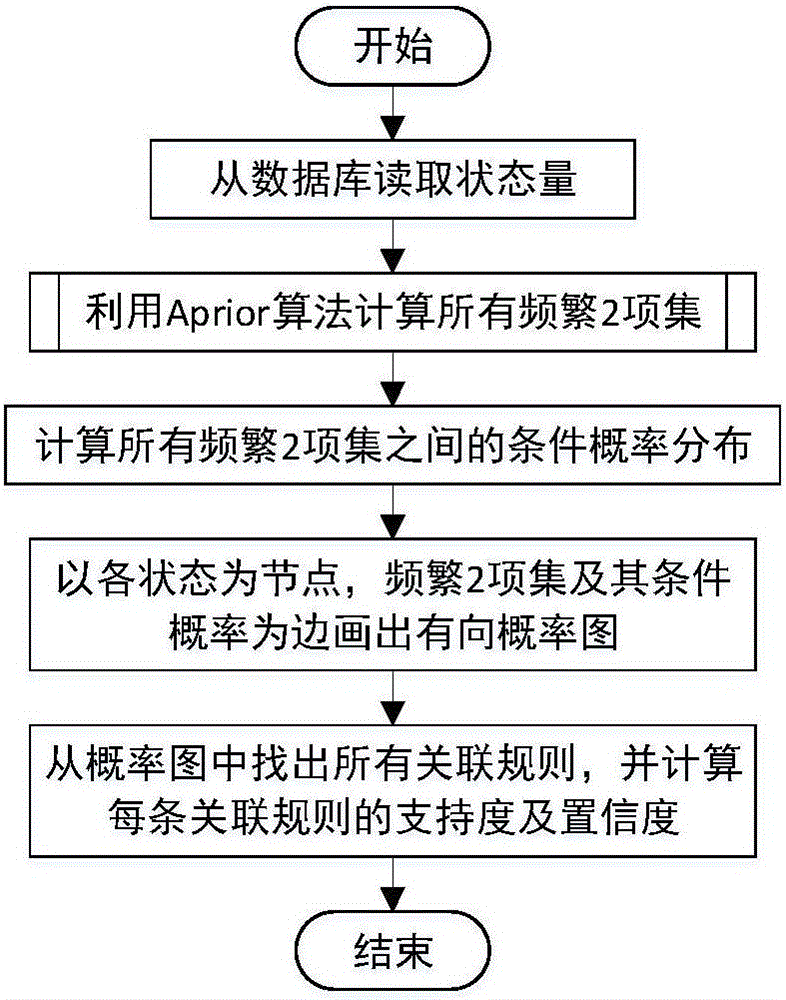
图1为本发明方法流程图；

图2(a)-(h)为变压器在线监测状态量的概率分布图；

图3(a)-(c)为变压器运行数据日最大值的概率分布图；

图4(a)-(c)为变压器运行数据日平均值的概率分布图；

图5(a)-(d)为变电站气象数据概率分布图；

图6为变压器各状态量间的概率图；

图7(a)-(d)为变压器各状态量之间的条件概率分布图；

图8(a)-(h)为变压器状态数据；

图9为变压器运行电流数据；

图10为状态预测结果对比示意图。

具体实施方式：

下面结合附图对本发明进行详细说明：

本发明将概率图模型引入对变压器状态进行关联规则挖掘。结合Apriori算法及概率图模型，提出一种新的关联规则挖掘算法，该算法首先利用Apriori算法找出所有的频繁二项集，然后利用概率图模型找出所有关联规则，并计算每项关联规则的支持度和置信度。该方法利用概率图分析关联规则，避免了搜索各阶频繁项集都需要循环扫描所有数据项。

概率图模型是图论和统计学相结合的产物，是一种数据驱动的图结构模型，对不确定性和复杂性问题提供了直观的方法。图模型提供了联合概率分布的结构表示，本文应用有向无环图(贝叶斯网络)模型来挖掘变压器各状态量间的关联规则。

贝叶斯网络是一个有向无环图，它提供了一种表示因果信息的方式，用图形模式表示了变量间的连接概率。建立贝叶斯网络的目的是描述变量间的关系进而进行概率推理。用概率进行不确定性处理能够保证结果的准确性。

考虑一个含有n个变量的集合X＝{X₁,X₂,…,X_n}，贝叶斯网络的链规则为依据条件概率链来表达联合概率，即：

贝叶斯网络中隐含着局部条件独立假设，即已知父节点时节点条件独立于其非子节点。利用该条件独立性，可对连规则进行化简。

贝叶斯网络主要由以下两部分构成，分别对应问题的定性和定量描述：

1.有向无环图(Directed Acyclic Graph,DAG)，由若干节点和有向边组成，节点代表随机变量，即待分析问题中的现象、状态或属性。有向边代表节点之间的依赖或因果关系，有向边的箭头代表因果关系的方向性，节点之间没有有向边连接表示对应的变量之间条件独立。

2.条件概率表(Condition Probability Table,CPT)，表示子节点与其父节点之间的关联强度，没有父节点的节点概率为其先验概率。

贝叶斯网络结构是将数据实例抽象化的结果。假定有一个包含n个变量的随机变量集V，G表示有向无环图，L表示边的边的集合，P表示条件概率分布集，则贝叶斯网络模型用数学符号表示为：

BN＝(G,P)＝(V,L,P) (2)

其中，

G＝(V,L) (3)

V＝{V₁,V₂,Λ,V_n} (4)

P＝{P(V_i|V₁,V₂,Λ,V_i-1),V_i∈V} (5)

根据链规则(1)，及条件独立性假设，用表示变量V_i的父节点集，则其联合概率分布为：

关联规则挖掘的目的是找出数据库中不同项之间的关联关系，下面定义关联规则挖掘中的几个重要概念：

1)关联规则挖掘的数据集记为D，D＝{t₁,t₂,L,t_n}，其中t_k＝{i₁,i₂,L,i_p}，,t_k(k＝1,2,L,n)称为事务，i_m(m＝1,2,…,p)称为项。每一个事务都有一个唯一的标识符，称为TID。

2)设I＝{i₁,i₂,…,i_p}是D中全体数据项组成的集合，I的任何子集X称为D中的项集，若|X|＝k，X为k-项集。若X∈t_k，称事务t_k包含项集X。

3)数据集D中包含项集X的事务数称为项集X的支持数，记为σ_X。项集X的支持度记为support(X):

其中，|D|是数据集D中的元素个数，若support(X)不小于最小支持度阈值(记为minSup)，则称X为频繁项集，否则称X为非频繁项集。

4)若X、Y为项集，且蕴含式称为关联规则，X、Y分别称为关联规则的前提和结论，项集XUY的支持度称为关联规则的支持度，记为即

关联规则的置信度记为

关联规则挖掘中需要根据需要指定最小置信度阈值，记为minConf。支持度用于衡量关联规则在整个数据集中的统计重要性，置信度用于衡量关联规则的可信程度。

本发明基于概率图的变压器状态关联规则挖掘方法的主要流程如图1所示，包括以下步骤：

(1)从数据库中读取设定变压器状态量数据；包括：变压器油色谱数据、油温数据、变电站气象数据等等；构建变压器状态量关联规则挖掘的数据集；

(2)利用Apriori算法，找出变压器状态量数据集中所有的频繁2-项集；Apriori算法采用逐层搜索的迭代方法，由候选项集生成频繁项集，最终由频繁项集得到关联规则。具体步骤如下：

1)将变压器状态量数据集记为D，D＝{t₁,t₂,L,t_n}，其中t_k＝{i₁,i₂,L,i_p}，则将t_k(k＝1,2,L,n)称为事务，i_m(m＝1,2,…,p)称为项；

2)扫描变压器状态量数据集中的所有事务，计算每项出现的次数，产生频繁1-项集L₁；按照上说频繁项集X的产生方法确定。

3)根据频繁1-项集L₁得到频繁2-项集L₂，具体方法如下：

Step1：连接和剪枝：对每两个有1个共同的项目的频繁项集进行连接得到C'₂，并根据频繁项集的反单调性，对C'₂进行剪枝，得到候选2-项集C₂；其中，两个频繁项集如果有相同的项目t_n称之为有共同的项目。

Step2：扫描变压器状态量数据集，确定每个事务t所含候选2-项集C₂的支持度subset(C₂,t),并存放在hash表中；

Step3：设定最小支持度阈值minSup，删除支持度低于minSup的项集，得到频繁2-项集L2。

(3)筛选频繁2-项集，并计算筛选后的所有频繁2-项集之间的条件概率分布；

由于当support(XUY)≈support(X)support(Y)时，两项集(X,Y)是相互独立的，故关联规则是无趣的。

2-项集X与Y的P-S兴趣度定义为：

1)若interest(X,Y)＞0，那么X和Y正相关；

2)若interest(X,Y)≈0，那么X和Y相互独立，从频繁2项集中删除；

3)若interest(X,Y)＜0，那么X和Y负相关。

(4)根据筛选后的频繁2-项集，以频繁2-项集及频繁2-项集之间的条件概率分布为边，构造概率图；

(5)根据所述概率图，找出所有的关联规则，生成关联规则集合；

(6)计算每一条关联规则的支持度和置信度，根据计算得到的支持度和置信度确定变压器各状态量之间的关联程度；若关联规则满足且称关联规则为强关联规则，否则称关联规则为弱关联规则。

将各状态量数据间的关联规则引入变压器状态预测，可以对预测结果进行修正。

算法的仿真及试验验证

以某五台500kV变电站的主变。为例分析变压器各状态量之间的关联规则。变压器各在线监测状态量，即油中溶解气体含量(包括：H₂、C₂H₂、CH₄、C₂H₄、CO、CO₂、碳水化合物)及油温的概率布图分别如图2(a)-(h)所示。

变压器的运行状态，即运行电流、有功功率、无功功率的每天最大值的概率分布图分别如图3(a)、(b)、(c)所示，其日平均值的概率分布图分别如图4(a)、(b)、(c)所示。

变电站的气象数据，气温、地面温度、相对湿度、平均风速的概率分布，分别如图5(a)、(b)、(c)、(d)所示。

将各状态量数值从其最小值到最大值分为10个区间段，若数值在某个区间段，认为事件发生，反之，认为事件不发生。对每个区间段，分别得到频繁2项集，画出概率图，如图6所示。

计算各状态量之间的条件概率分布，以乙炔相对氢气的条件概率分布、油温相对气温概率分布、乙炔相对总烃条件概率分布、油温相对平均电流的概率分布为例分别如图7(a)-(d)所示。

频繁集项数大于3的关联规则，及其最大支持度和最大置信度，如表1所示。

表1变压器状态数据关联规则挖掘结果

某500kV变压器从2010年3月21日至2013年6月28日，共1200天的油色谱、油温和环境温度数据如图8(a)-(h)所示。负载电流数据如图9所示。

径向基神经网络(Radical Basis Function Neural Network)是一种三层前向神经网络。第一层为输入层，第三层为输出层。第二层为隐藏层，隐藏层中的神经元变换函数即径向基函数是对中心点径向对称且衰减的非线性函数，该函数将低维的输入矢量变换到高维空间内，使得在低位空间内的线性不可分的问题在高维空间内线性可分。RBF神经网络不仅具有全局逼近的性质、良好的泛化能力，而且计算量小，学习速度快，不存在局部最小问题。因此已经广泛地应用在时间序列分析、模式识别等领域。

由于输入层仅仅起到传输信号的作用，也就是说输入层和隐藏层之间可以看作连接权值为1的链接，所以网络的学习过程是通过修改连接隐藏层和输出层的权值来实现的。

将图8(a)-(h)、图9中的数据作为神经网络的输入，预测该变压器以后360天的运行电流数据，神经网络每30天更新一次。将表1中得到的状态量间的关联规则作为先验知识对神经网络输出层权值进行人工调整。得到的油温、变压器油中乙炔含量及油中总烃含量的预测相对误差如图10(a)-(c)所示。

从图10(a)-(c)中可以观测到，将经过数据挖掘得到的数据间关联规则引入状态预测对预测结果进行修正可以显著提高预测精度：平均预测误差从20％下降到了10％。进而证明了本文所提出的关联规则挖掘方法可以有效地挖掘出变压器各状态量之间的关联规则。

上述虽然结合附图对本发明的具体实施方式进行了描述，但并非对本发明保护范围的限制，所属领域技术人员应该明白，在本发明的技术方案的基础上，本领域技术人员不需要付出创造性劳动即可做出的各种修改或变形仍在本发明的保护范围以内。