一种彩色图像的低嵌入率压缩感知通用隐写分析方法与流程

本发明涉及图像处理及其信息安全领域，具体来说涉及一种对彩色图像的低嵌入率压缩感知通用隐写分析方法。

背景技术：

隐写分析是隐写的攻击过程，目的是为了揭示数字媒体中隐藏的秘密信息，或者指出秘密信息的存在性。隐写分析技术在一定程度上可以看成是两类分类的模式识别问题，关键因素是特征选择。隐写新方法的出现进一步提高了检测的难度，研究并实现更为有效的检测方法是对隐写分析提出的新问题。即使是简单的LSB替换嵌入，对于较低嵌入率的检测也是十分困难的。这里所谓的嵌入率(ER),就是嵌入的比特位与图像的像素量的比值。例如当秘密信息是1k字节嵌入空域图像时,如其像素量为50k,则嵌入率ER＝(1×8)/50＝0.16bpp(bpp是bit perpixel的缩写)；当8比特位秘密信息嵌入到一个8×8大小的DCT块时,则嵌入率ER＝0.125bpp。经典的Westfeld隐写分析方法具有检测极低嵌入率的能力，但仅限于对曾经JPEG压缩而且后来未经缩放等处理的彩色图像。

近年来对低嵌入率的隐写分析方法有些新的进展，在早期卡方分析和RS等方法之后，先后提出了一些基于像素对的隐写分析方法。其基本原理是基于有限状态机，有限状态机的状态是选择的抽样对的多重集。如果样本对是从数字化的连续信号中抽取出来的，对于自然图像而言，相邻像素对所构成的多重集之间有着某种固定的关系。随机LSB替换隐写分析会引起这些多重集的改变，从而改变多重集的统计关系。SPA作为LSB分析的有效方法明显优于RS法，引起了研究者的关注。随后即出现了对SPA的推广和拓展，这方面的工作以Ker的研究最具代表性。通过将SPA中仅考虑基于像素对(即二元组)的分析，推广到三元组，对于低嵌入率的隐蔽信息嵌入量估计质量明显提高了。

近来Barbier、黄炜等提出了一种针对JPEG图像的隐写分析方法，可检测用Out Guess、F5、Hide and Seek极小嵌入量隐写所生成的载密图像(可参见文献[Barbier J,Filiol E,Mayoura K.New features for specific JPEG steganalysis]、[World Academy of Science,Engineering and Technology,2006,2(3):72-77])。惠卯卯等针对JPEG图像隐写方法，从特征加权融合的角度设计了一种分类器[8]。该方案首先对DCT域块内系数分别进行横向、纵向和zigzag差分运算,使用马尔科夫转移矩阵挖掘差分系数间的关联，生成局部马尔科夫特征，然后依据各向特征对分类器的贡献程度设置权重，最后生成加权平均特征并使用支持向量机进行分类。实验结果验证了该方案的有效性，对嵌入率为0.05时的四种隐写方法(F5、Outguess、MB1和MB2)其检测率均高于91％，同时特征融合方法没有增加特征维数。

周治平等针对现有典型的通用隐写分析方法提取特征时多数对图像进行正交小波分解中的不足，提出了一种新的利用小波包分解和遗传算法的高效的隐写检测方案(参见[惠卯卯,周治平.基于加权融合和马尔科夫矩阵的JPEG图像隐写分析[J].计算机应用研究,2009,26(12):4790-4792])。该方法首先对原灰度图像及其预测误差图像运用小波包分解生成多个子带，提取各子带系数直方图特征函数多阶矩作为特征，将支持向量机的分类效果作为自适应度函数值返回，指导遗传算法搜索最优的特征选择方案。针对Outguess、F5、MB1载密图像与载体图所组成的混合图像库上的仿真实验结果表明：该方法比现有的隐写分析方法，平均检测率提高了约1％-17.8％(参见[周治平,张小祥，,惠卯卯.小波包子带频率矩和遗传算法的图像隐写分析[J].系统工程理论实践,2010,30(10):1864-1869]、[HosseinAmirkhani,MohanmmadRahmati.New framework for using image contents in blind steganalysis systems[J].Journal of electronic imaging,2011,20(1):1-14.])。

近年来出现的压缩感知理论(Compressed Sensing，CS)是信号处理和数学领域中新出现的重要理论，本质是对稀疏或可压缩信号(如图像)，能够以高概率由少量测量数据恢复整个信号。其主要思想是采用过完备字典代替传统的正交基函数揭示信号的内在结构，并能够通过稀疏表示、非相干测量和重构算法(目前主要是凸优化算法和贪婪算法)恢复原始信号。

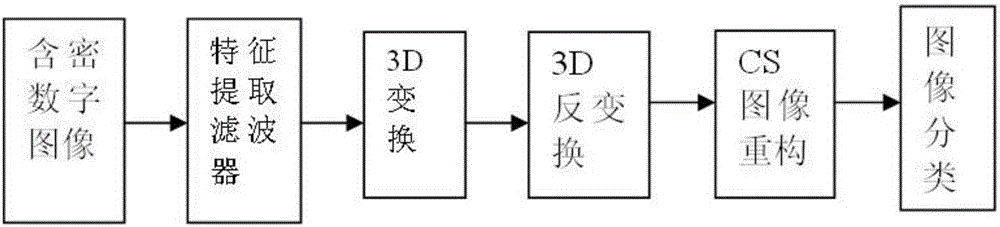
由于数字图像内容的通用隐写分析的重点在于结构分析和特征提取，而CS技术具有采样数据量少、结构特征明显和高概率恢复信号的特性，所以，适合低嵌入率下对图像信号的数据处理、秘密信息提取的要求，如在文献[C Patsakis,N G Aroukatos,“LSB and DCT Steganographic Detection Using Compressive Sensing,”Journal of Information Hiding and Multimedia Signal Processing,vol.5,no.1,(2014),pp.20-32.]中，C Patsakis等结合CS技术与BM3D滤波器技术，提出了一种LSB和DCT域的隐写分析方法，图1为该方法的实现原理，包括图1(a)图像训练过程和图1(b)图像检测过程。该方法的实验结果验证了有效性，对嵌入率为0.08时的LSB和DCT两种隐写方法，其检测率均高于93％。。

如图1所示C Patsakis等提出的方法说明CS技术的应用较好地提取了数字图像的特征数据，且提高了隐写分析的识别率。

经过国内外的相关研究机构和大批科研人员的十多年的努力奋斗，在隐写分析方面取得了一些研究成果，但是隐写分析的研究仍然处于理论研究阶段，成熟的技术尚未形成，特别是，结合CS技术的隐写分析更是处于探索过程。而C Patsakis等提出的基于CS技术实现隐写分析技术(参见[C Patsakis,N G Aroukatos,“LSB and DCT Steganographic Detection Using Compressive Sensing,”Journal of Information Hiding and Multimedia Signal Processing,vol.5,no.1,(2014),pp.20-32])，存在如下缺点：

(1)现有的CS通用隐写分析技术是基于BM3D滤波器的原理，提取对嵌入秘密信息敏感的图像特征时，并未给出分块感知的结果或者DCT有效利用系数。而通用隐写分析技术受到较大影响的是对原始图像和载密图像进行预处理、特征提取之后进行分类。

(2)现有的CS隐写分析方法只针对LSB和DCT域的灰度图像隐写算法，需要利用3D数据矩阵实现，不具备鲁棒的通用性。

针对上述2种问题，本发明需要解决如下问题：利用分层方式对彩色数字图像HSV(Hue,Saturation,Value)进行分层映射，获取图像分层HSV特征，同时利用共生矩阵分层出纹理特征，并基于二维压缩感知的测量矩阵提取图像的二类特征值，最后根据三层前馈非线性神经网络确定秘密信息的存在，解决低嵌入率的隐写分析检测精度问题。

技术实现要素：

本发明从二维压缩感知的矩阵模型和隐写分析的检测精度出发，提出了一种针对彩色图像的低嵌入率压缩感知(CS)通用隐写分析方法,其目的是从隐写分析的特征提取与数据处理的根本问题上为信息安全探索一种新的发明成果。

本发明采用如下技术方案实现上述发明目的：

一种彩色图像的低嵌入率压缩感知通用隐写分析方法，包括如下内容：

(1)构建二维压缩感知(2D-CS)测量模型；

(2)构建二维图像HSV分层表示模型；

(3)拟灰度共生矩阵与分层纹理特征分析。

所述(1)构建二维压缩感知(2D-CS)测量模型具体包括如下内容：

对于N×N的RGB图像X，数字图像的二维信号X∈R^N×N，是二维可稀疏信号；

设Φ₁,Φ₂∈R^M×N分别是行、列压缩测量矩阵，对行、列向量同时进行压缩测量，构建2D压缩测量的过程如下二维测量模型公式(1)：

Y＝Φ₁XΦ₂^T (1)

其中X∈R^N×N代表二维图像信号，Y∈R^M×M代表二维压缩测量值；

测量矩阵Φ₁与Φ₂的选择：设Gauss随机矩阵G＝(g_ij)_M×N＝(G₁,G₂,...G_N)，其矩阵元素g_i,j服从均值为零、方差为的正态分布，并且元素间相互独立，选取矩阵G的元素满足如下分布：通过对Gauss随机矩阵进行列归一化处理，选定测量矩阵Φ₁＝Φ₂＝Φ，其构造如下公式(2)所示：

所述(2)构建二维图像HSV分层表示模型具体包括如下内容：

①进行二维图像的HSV空间网格离散化处理；

②获得分层映射算子；

③分层映射矩阵与分层HSV特征分析：

④分层HSV特征的可区分性分析。

所述①进行二维图像的HSV空间网格离散化处理具体包括如下内容：

进行二维图像的HSV空间网格离散化处理设HSV空间的取值范围分别为三个分量分别选取离散点集ST₁,ST₂,ST₃进行区间划分，离散点集如下：

图像的HSV颜色空间被分割成较小的立方体网格：

其中：i＝1,2,…,L1；j＝1,2,…,L2；k＝1,2,…,L3。

所述②获得分层映射算子具体包括如下内容：对HSV空间的立方体网格按照行优先次序排序，得到立体方序列：V_l(l＝1,…,L；L＝L₁×L₂×L₃)，其中V_l＝V_ijk l＝(i-1)L₁+(j-1)L₂+k为定义的分层映射算子；在V_l上对原始图像进行分层映射，得到的分层映射矩阵LAY_l(X)＝(LAY_l(i,j))_N×N为：

其中l＝1,2,…,L；i,j＝1,2,…,N；

所述③分层映射矩阵与分层HSV特征分析具体包括如下内容：

采用二维测量模型公式(1)，选取归一化Gauss随机矩阵Φ₁，Φ₂∈R^M×N(M<<N)，对二维信号LAY_l(X)进行二维压缩感知测量，得到采样值如下：

Y_l＝Φ₁LAY_l(X)Φ₂^T∈R^M×M (8)

其中l＝1,2,…,L；

这里，Y_l∈R^M×M作为原始二维图像X的第l层分层映射矩阵的二维压缩感知测量值；

采用PCA方法对矩阵Y_l列向量所构成向量集进行分析：

设矩阵Y_l的列向量表达形式为：

计算基于列向量集的协方差矩阵：

其中：

由于矩阵C_v是对称矩阵,其M个特征值都是实数；计算矩阵C_v的特征向量与特征值，把特征值按降序排列后形成图像第l层上的内容特征向量：

λ_l,1≥λ_l,2≥,...,≥λ_l,M

由此，第l层的分层HSV特征向量定义为

其中l＝1,2,…,L代表分层的层数。

所述④分层HSV特征的可区分性分析具体包括如下内容：将图像划分成两个子图T，T'，针对子图T，T'，进行分层压缩测量特征差异的计算：

假设红色分层在第l层上，经过分层映射后，得到如下的分块矩阵：

其中I，0分别代表N/2×N/2的单位矩阵和零矩阵；

对测量矩阵Φ₁，Φ₂∈R^M×N也做如下分块：

Φ₁＝[Φ₁₁Φ₁₂],Φ2＝[Φ₂₁Φ₂₂]

其中Φ₁₁，Φ₁₂，Φ₂₁，Φ₂₂∈R^M×(N/2)；

针对子图T，T'，采用公式(8)得到如下的分层二维压缩感知测量值：

在第l层上，子图T，T'的特征感知数据的差异计算如下：

其中c₀是只与测量矩阵Φ₁，Φ₂相关的常数。

所述(3)拟灰度共生矩阵与分层纹理特征分析具体包括如下内容：拟灰度共生矩阵与方向θ和距离d这两个参数有关，其定义为公式(15)-(16)：

其中l₁,l₂＝1,…,L代表分层的层数，#(·)表示集合基数；方向θ和距离d参数可选取如下序列：θ＝θ_i；i＝1,2,…,L₄；d＝d_j；j＝1,2,…,L₅；

矩阵M(θ,d)是二维可稀疏信号，采用公式(1)的二维压缩感知模型进行测量，得到与纹理相关的分层测量值：

其中l＝(i-1)×L₄+j；i＝1,2,…,L₄；j＝1,2,…,L₅；l＝1,2,…,L₆；L₆＝L₄×L₅；

采用类似分层HSV特征向量的计算过程，对于与纹理有关的分层映射矩阵MY_l的列向量集，采用公式(10)计算其相应的协方差矩阵，获取相应协方差矩阵M个特征值并按照降序排列，得到在第l层上基于拟灰度共生矩阵的分层纹理特征向量，记为

其中l＝1,2,…,L₆代表层数；i＝1,2,…,M是矩阵MY_l列向量集协方差矩阵的第i个特征值；由公式(11)和公式(18)生成的向量序列形成了数字图像的分层HSV特征向量和分层纹理特征向量共两类特征向量。

本发明对比现有技术，有如下优点：

通过对数字图像通用隐写分析和低嵌入率隐写算法的相关研究，本发明提供一种彩色图像的低嵌入率压缩感知通用隐写分析方法，主要解决如下问题：

(1)通过压缩感知(Compressive Sensing,CS)域的数据统计技术，解决数字图像隐写算法的通用隐写分析盲检测问题。

(2)通过对目前的基于LSB和DCT域的CS隐写分析进行研究，解决JPEG和BMP图像格式在传统的F5，Outguess，MB1，MB2，Jsteg等不同隐写算法下低嵌入率的隐写分析检测精度问题。

附图说明

图1是现有技术CS技术实现隐写分析的原理；

图2是本发明彩色图像低嵌入率压缩感知的通用隐写分析实现原理；

图3 HSV空间分割与分层映射图；

图4分层测量特征差异分析图。

具体实施方式

本专利基于CS技术，采用二维压缩测量模型，设计满足RIP条件的行列测量矩阵，通过分层方式对彩色数字图像HSV(Hue,Saturation,Value)进行分层映射，获取图像分层HSV特征及分层纹理特征，建立了一种基于二维压缩感知的分层HSV特征的图像检索框架。通过图像HSV空间上的离散划分与分层映射算子，发明了提供一种基于网络空间的拟灰度共生矩阵，采用二维压缩测量过程生成图像压缩测量值并构成矩阵，结合采用PCA(Principal Component Analysis)方法获取协方差矩阵特征值序列，作为图像的两类内容特征向量，最后应用三层前馈非线性神经网络作为含密图像的判决分类器，整个系统的功能结构如图2所示。

本发明方法的具体包括如下内容：

(1)二维压缩感知(2D-CS)测量模型

对于N×N的RGB图像X，数字图像的二维信号X∈R^N×N，设Ψ∈R^N×N为在离散余弦变换(DCT)、离散傅里叶变换(DFT)、离散小波变换(DWT)等变换基底所组成的矩阵，则S＝Ψ^TXΨ或者X＝ΨSΨ^T，变换后系数矩阵S∈R^N×N的高频系数大部分接近于零，数字图像X∈R^N×N是二维可稀疏信号。

为了解决把一维CS理论应用于二维(2D)图像分析时所导致的维数问题以及图像像素点之间的相对位置关系丢失的问题，本方法采用2D压缩感知模型(参见[Gao Chen,Defang Li,Jiashu Zhang.Iterative gradient projection algorithm for two-dimensional compressed sensing sparse image reconstruction[J].Signal Processing,2014,104:15-26.])。设Φ₁,Φ₂∈R^M×N(M<<N,M是测量值的大小)分别是行、列压缩测量矩阵，对行、列向量同时进行压缩测量，构建2D压缩测量的过程如下：

Y＝Φ₁XΦ₂^T (1)

其中X∈R^N×N代表二维图像信号，Y∈R^M×M代表二维压缩测量值。若Φ₁、Φ₂是归一化高斯(Gauss)随机测量矩阵，则以接近1的概率满足RIP(Restricted Isometry Property)条件，其中代表矩阵的Kronecker积。由二维测量值Y计算一个等价L1范数的优化问题能够恢复二维信号量X。这意味着在2D压缩感知测量模型(1)中，只要测量矩阵Φ₁与Φ₂选取合适，用少量二维测量值Y可以作为原始图像的一类内容特征。

测量矩阵Φ₁与Φ₂的选择：测量矩阵的构造方法通常有三种:随机矩阵、结构随机矩阵与确定性矩阵。在随机构造法中，Gauss随机矩阵是压缩感知研究中最常用的测量矩阵，它能以高概率满足RIP条件，同时它产生的测量值数目比较少，对于长度为N，稀疏度为K的信号，仅需要M≥cKlog(N/K)个测量值就可以高概率地重构出原始信号。设Gauss随机矩阵G＝(g_ij)_M×N＝(G₁,G₂,...G_N)，其矩阵元素g_i,j服从均值为零、方差为的正态分布，并且元素间相互独立，选取矩阵G的元素满足如下分布：通过对Gauss随机矩阵进行列归一化处理，选定测量矩阵Φ₁＝Φ₂＝Φ，其构造如下公式(2)所示：

(2)二维图像HSV分层表示模型

二维图像HSV表示方法包含了色调、饱和度和亮度三个分量，在色彩分辨能力方面，用HSV表达图像更接近人类对颜色概念的理解，因此较广泛应用于计算机图像分析与视觉计算等领域。本方法采用颜色空间变换把大小为N×N的RGB图像X，从RGB颜色空间变为HSV颜色空间进行表达。

①图像HSV空间分层原则：针对图像HSV空间进行三维网格离散化处理，把图像像素值与像素点分布情况进行联合分析，通过分层映射获取分层映射矩阵，该分层映射矩阵反映了图像像素值某个网格邻域内的相应像素点在平面上位置分布状况，采用二维压缩测量与PCA过程，从而获取图像的分层全局特征作为图像检测分类的重要内容特征。

②二维图像的HSV空间网格离散化处理：设HSV空间的取值范围分别为三个分量分别选取离散点集ST₁,ST₂,ST₃进行区间划分，离散点集如下：

图3所示，图像的HSV颜色空间被分割成较小的立方体网格：

其中：i＝1,2,…,L1；j＝1,2,…,L2；k＝1,2,…,L3。

③分层映射算子：对HSV空间的立方体网格按照行优先次序排序，得到立体方序列：V_l(l＝1,…,L；L＝L₁×L₂×L₃)，其中V_l＝V_ijkl＝(i-1)L₁+(j-1)L₂+k为定义的分层映射算子。在V_l上对原始图像进行分层映射，得到的分层映射矩阵LAY_l(X)＝(LAY_l(i,j))_N×N为：

其中l＝1,2,…,L；i,j＝1,2,…,N。

④分层映射矩阵与分层HSV特征：在HSV网格V_l上，分层映射矩阵LAY_l(X)反映了图像HSV空间邻域内的像素点在平面坐标上相对位置的分布状况。前面已经指出，图像在离散余弦变换(DCT)、离散傅里叶变换(DFT)、离散小波变换(DWT)下是二维可稀疏信号。而第l层上分层映射矩阵LAY_l(X)是原始图像的一个映射子集，因此也是一个可稀疏的二维信号。采用二维测量模型公式(1)，选取归一化Gauss随机矩阵Φ₁，Φ₂∈R^M×N(M<<N)，对二维信号LAY_l(X)进行二维压缩感知测量，得到采样值如下：

Y_l＝Φ₁LAY_l(X)Φ₂^T∈R^M×M (8)

其中l＝1,2,…,L。

这里，Y_l∈R^M×M作为原始二维图像X的第l层分层映射矩阵的二维压缩感知测量值，它集中体现了图像的形状、区域等内容特征。

为了进一步说明分层映射矩阵Y_l所蕴含的内容特征，采用PCA方法对矩阵Y_l列向量所构成向量集进行分析。设矩阵Y_l的列向量表达形式为：

计算基于列向量集的协方差矩阵：

其中：

由于矩阵C_v是对称矩阵,其M个特征值都是实数。计算矩阵C_v的特征向量与特征值，把特征值按降序排列后形成图像第l层上的内容特征向量：

λ_l,1≥λ_l,2≥,...,≥λ_l,M

由此，第l层的分层HSV特征向量定义为

其中l＝1,2,…,L代表分层的层数。

⑤分层HSV特征的可区分性：分层二维压缩感知测量值Y_l∈R^M×M及对应特征向量比传统颜色直方图具有更好可区分性。设有如图4所示的两个子图T，T'。

把子图T，T'划分为大小N/2×N/2的4个子块，子图T的左上角子块与子图T'的左下角子块有红色对角线，其它子块的颜色都相同。按照颜色直方图进行计算，这两个子图对应的传统颜色直方图完全一样。

针对子图T，T'，下面说明本发明的分层压缩测量特征差异的计算方法。

假设红色分层在第l层上，经过分层映射后，得到如下的分块矩阵：

其中I，0分别代表N/2×N/2的单位矩阵和零矩阵。

对测量矩阵Φ₁，Φ₂∈R^M×N也做如下分块：

Φ₁＝[Φ₁₁Φ₁₂],Φ2＝[Φ₂₁Φ₂₂]

其中Φ₁₁，Φ₁₂，Φ₂₁，Φ₂₂∈R^M×(N/2)。

针对子图T，T'，采用公式(8)得到如下的分层二维压缩感知测量值：

在第l层上，它们的特征感知数据的差异计算如下：

其中c₀是只与测量矩阵Φ₁，Φ₂相关的常数。

公式(14)是子图T，T'的分层压缩测量值Y_l以及相应的特征向量它们保留了颜色分层邻域与像素点的位置关系，能够体现含密图像与非含密图像更精细化的差异，比传统的颜色直方图具有更好可区分性。

(3)拟灰度共生矩阵与分层纹理特征

传统灰度共生矩阵是用来描述纹理特征的经典数据结构，是关于图像灰度级在空间分布上的综合描述，通过提取有意义的统计特性来表达图像的纹理特征。灰度共生矩阵的构造依赖于像素点之间的方向和距离这两个参数。在HSV空间网格划分基础上，本发明的基于网格划分的拟灰度共生矩阵是关于图像网格邻域在空间分布上的综合描述。拟灰度共生矩阵与方向θ和距离d这两个参数有关，其定义为公式(15)-(16)：

其中l₁,l₂＝1,…,L代表分层的层数，#(·)表示集合基数。方向θ和距离d参数可选取如下序列：θ＝θ_i；i＝1,2,…,L₄；d＝d_j；j＝1,2,…,L₅.当参数θ,d选取不同角度、不同距离的参数时，矩阵M(θ,d)可以看作是传统灰度共生矩阵的推广，它集中反映了HSV空间分层图邻域间的纹理特征。

矩阵M(θ,d)是二维可稀疏信号，采用公式(1)的二维压缩感知模型进行测量，得到与纹理相关的分层测量值：

其中l＝(i-1)×L₄+j；i＝1,2,…,L₄；j＝1,2,…,L₅；l＝1,2,…,L₆；L₆＝L₄×L₅。

采用类似分层HSV特征向量的计算过程，对于与纹理有关的分层映射矩阵MY_l的列向量集，采用公式(10)计算其相应的协方差矩阵，获取相应协方差矩阵M个特征值并按照降序排列，得到在第l层上基于拟灰度共生矩阵的分层纹理特征向量，记为

其中l＝1,2,…,L₆代表层数。i＝1,2,…,M是矩阵MY_l列向量集协方差矩阵的第i个特征值。由公式(11)和公式(18)生成的向量序列形成了数字图像的分层HSV特征向量和分层纹理特征向量共两类特征向量。

(4)分类器的设计

对于HSV空间，当图像两类特征被提取出来后，能否判定是否含有秘密信息是一个二类分类的问题。

在本发明中，采用了三层前馈非线性神经网络来作为分类器(参见[Lie Wen-Nung,Lin Guo-Shiang.A featu re-based classification technique for blind image st eganalysis.IEEE Transactions on Multimedia,2005,vol.7,no.6,pp:1007-1020.])。在输入层是两个神经元，即是压缩感知技术提取出来的二维特征向量输出层是一个神经元，即是分类结果有或无；中间层是由若干个神经元组成，用来记忆训练样本集的。在多层神经网络中，本专利采用C型螺线函数g(x)＝1/(1+exp(-x))作为分类因子。螺线函数g(x)的值域为(0.0,1.0)，当输出值靠近1时，就将测试图像判为含密图像。相反地，当输出值靠近0时，就将测试图像判为非含密图像。

当然,分类前首先要决定是空域图像还是DCT、DFT以及DWT变换域图像(JPEG图像)，因为不同格式的图像特征不同，分类器的隐含层结构不同。

对于彩色图像，则在每个空间都有一个二维特征向量，如HSV在R、G、B空间都有一个特征向量，对变换域格式图像，在Y、Cr、Cb空间也都有一个特征向量。对每个空间层都要设定一个三层前馈非线性神经网络分类器。根据选举法，如果二个空间内判为含密或非含密，则就判为图像掩密或干净。

利用本发明方法进行具体实验过程如下：

(1)实验条件和结果1

本实验使用的图像库中有4000多幅原始彩色图像，其中BMP、GIF空域格式的图像各1000多幅，JPEG图像2000多幅。用表1列出10种(5种空域隐写工具，5种DCT域隐写工具)不同隐写工具嵌入信息后得到掩密图像各1000幅。训练时采用空域图像1000幅干净图像(其中BMP、GIF各500幅)，2500幅用5种空域隐写工具嵌入秘密所得的掩密图像；同样地，DCT域图像1000幅干净图像和2500幅用5种DCT域隐写工具嵌入秘密信息后所得的掩密图像用作训练，剩余图像用作测试图像，并用Photoshop制作了空域图像和DCT域图像经平滑去噪、锐化、缩小、剪切(只做空域图像)、再压缩(只做JPG图像)各100幅，以供测试。

实验时利用的一些检测性能指标的概念说明如下：

阳性检测PD(Positive Detect ion)：正确地识别含密图像。

阴性检测ND(Negative Detect io n)：正确地识别原始图像。

假阳性(或虚警)FP(False Posit ive)：将原始图像误判为含密图像。

假阴性(或漏警)FN(False Negat iv e)：将含密图像误判为原始图像。

表1隐写工具与嵌入率

表2列出对不同隐写算法实现的隐写分析结果。表中的操作域那一项中，空域阳性检测率就是5种空域隐写方式的平均阳性检测率。同样，DCT域阳性检测率是5种DCT域隐写方式平均的阳性检测率。

表2不同隐写方式、不同操作域、不同处理和原始图像的平均PD、ND、FN和FP率

(2)实验条件和结果2

本实验从NRCS图像库(参见[Natural Resources Conservation Service.NRCS Photo Gallery Home[EB/OL].2010.6.12.http://photogallery.nrcs.usda.gov])和华盛顿大学的CBIR图像库中随机抽取1096幅JPEG图像作为原始图像，把这些图像剪裁成768×512或者512×768大小。用F5，Outguess，MB1，MB2，Jsteg嵌入算法进行嵌入，嵌入量分别为0.5KB，1KB，2KB。形成原始图像与嵌入图像18个实验组对。从每个组对中随机抽取896个图像对，对三层前馈非线性神经网络进行训练。每个组对剩下的200个图像对作为测试图像。为了减小随机取值带来的误差，实验采用10次平均的方法减小误差。

实验数据检测结果见表3。表中tn表示正确识别原始图像的概率，tp表示正确识别载密图像的概率，t表示平均检测率t＝(tp+tn)/2。

从表3中可以看出本专利方法对嵌入量为0.5KB有较好的检测率，而其他几种方法未考虑此种情况；当嵌入量分别为1KB和2KB的时候，检测准确性高于前三种算法。

表3 4种算法的检测结果(检测率％)

本发明为了更好地利用CS技术处理数字图像的长处，进一步提高隐写分析的数据处理效率和分类判断精度，提出的基于CS技术实现数字图像的低嵌入率压缩感知通用隐写分析的有如下优点：

(1)在图像HSV空间上引入网格离散和分层映射的原理，发明了一种基于HSV网格空间的拟灰度共生矩阵。这种拟灰度共生矩阵能够充分表示图像的纹理结构和图像的形状、区域等内容特征，能够精确计算含密图像与非含密图像特征数据的差异性。

(2)通过归一化Gauss随机矩阵作为测量矩阵，采用二维压缩感知(2D-CS)测量模型对HSV分层映射矩阵、拟灰度共生矩阵进行感知采样，并结合PCA方法提取了图像的分层HSV特征与分层纹理特征。二维压缩感知结合PCA技术实现了图像内在结构的数据描述，为三层前馈非线性神经网络提供了高效的训练数据，提高了后端隐写分析的检测精度。

本发明的实施方式不限于此，在本发明上述基本技术思想前提下，按照本领域的普通技术知识和惯用手段对本发明内容所做出其它多种形式的修改、替换或变更，均落在本发明权利保护范围之内。