一种基于GA‑ELM算法的铝合金压铸件晶粒尺寸预测方法与流程

本发明涉及铝合金压铸成型控制领域，特别是涉及一种基于GA-ELM算法的铝合金压铸件晶粒尺寸预测方法。
背景技术：
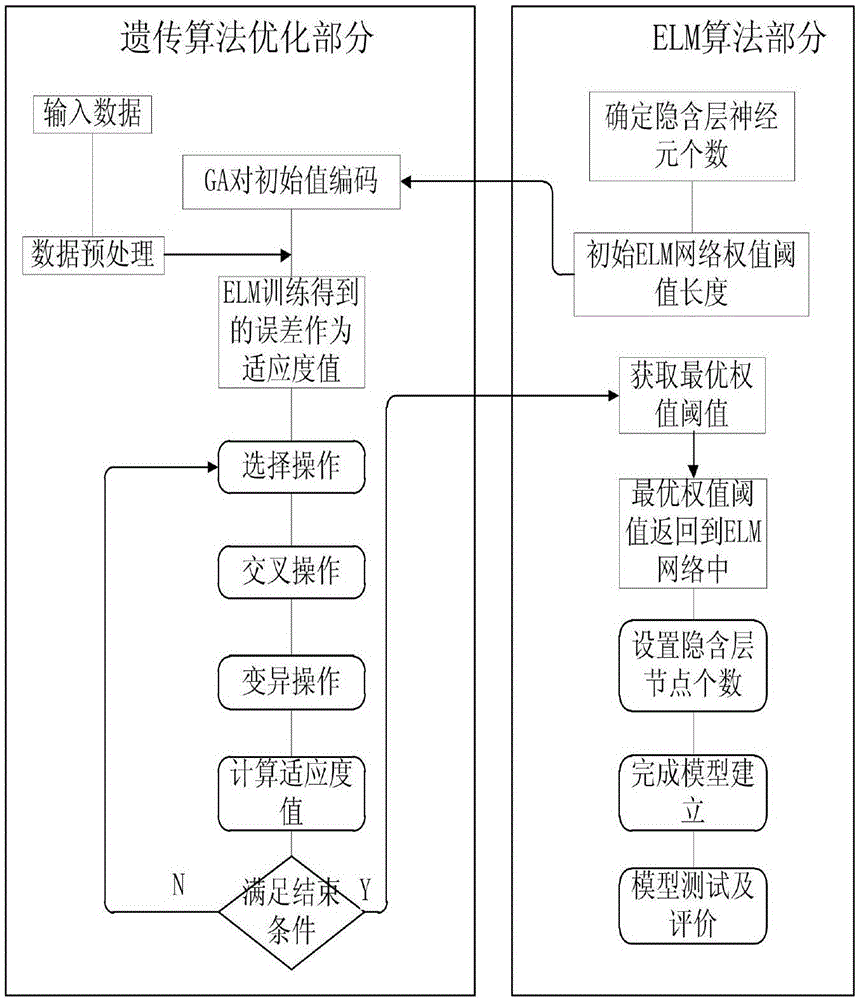
：铝合金压铸件广泛应用于汽车、飞机等装备制造业，压铸件质量将直接决定装备产品的质量。我们在避免铝合金压铸件缺陷的同时，压铸件本身的机械性能也同样值得重视，压铸件机械性能越高，则压铸件使用寿命越长，可靠性越高，进而影响整体装配产品的寿命及可靠性。决定材料机械性能最本质的因素是铸件内部晶粒的形貌、大小、取向和分布等微观组织情况。铝合金在压铸凝固的过程中，受不同压铸工艺条件的影响，凝固后的微观组织有所不同，微观组织的改变对压铸件的机械性能有强烈的影响，微观组织的控制是获得高质量压铸件的关键。晶粒尺寸的影响，实质是晶界面积大小的影响。晶粒越细小则晶界面积越大，对性能的影响也越大。对于金属的常温力学性能来说，一般是晶粒越细小，则强度和硬度越高，同时塑性和韧性也越好。这是因为，晶粒越细，塑性变形也越可分散在更多的晶粒内进行，使塑性变形越均匀，内应力集中越小；而且晶粒越细，晶界面越多，晶界越曲折；晶粒与晶粒中间犬牙交错的机会就越多，越不利于裂纹的传播和发展，彼此就越紧固，强度和韧性就越好。本研究内容针对的汽车空压机端盖在常温下工作，通常满足晶粒越细越好。因此在实际的压铸工艺制定过程中，要在考虑到压铸件缺陷最小的同时，选取晶粒尺寸最小的压铸工艺参数，以保证获得高质量的铝合金压铸件。传统的晶粒尺寸的预测方法包括利用模拟软件进行模拟、经验法以及BP神经网络、支持向量机、原始极限学习机等非线性预测等方法。模拟软件进行模拟精度较高，但是耗时非常长，效率低；经验法就是工程师直接根据以往的工程经验估计晶粒尺寸，预测时间段、效率高，但是这种方法要求工程师必须经验丰富，即使如此，预测精度也不高；BP神经网络存在易陷入局部最优解、网络结构不易确定；支持向量机的参数确定困难；原始极限学习机具有参数设置少，学习速度快，泛化性能好的优点，但是该算法随机产生输入层与隐含层间的权值矩阵及隐含层偏移量，初始权值、阈值参数对结果影响较大，不易获得最优ELM模型进行预测，实验法就是对每组工艺样本数据进行实际生产验证，这种方法不仅预测效率极低，而且成本高昂。因此，我们需要找到一种适用于这类复杂问题的新方法，准确、高效地预测铝合金压铸件晶粒尺寸等微观组织参数。技术实现要素：本发明要解决的技术问题是：提供一种基于GA-ELM算法的铝合金压铸件晶粒尺寸预测方法，低成本、高效率、高精度，以解决现有技术中存在的问题。本发明采取的技术方案为：一种基于GA-ELM算法的铝合金压铸件晶粒尺寸预测方法，该方法包括以下步骤：(1)参数确定：选取模具预热温度、压射温度、低速充型速度、高速充型速度的工艺参数作为输入参数；(2)通过软件模拟或实验的方法获取预测的数据样本，将数据样本分为训练集和测试集；(3)使用遗传算法(GA)优化极限学习机(ELM)的初始权值和阈值，从而获得新算法GA-ELM算法；(4)使用步骤(2)中获得的训练集数据样本对步骤(3)中的GA-ELM新算法进行训练，其中作为训练效果评价指标的个体适应度值选为训练集数据样本中最后六组样本数据对应的晶粒尺寸的预测误差平均值；(5)对步骤(4)训练好后的GA-ELM晶粒尺寸预测模型进行测试，将测试样本数据输入到GA-ELM模型中，将GA-ELM模型输出的预测值与测试集的实际值进行对比，评价GA-ELM模型的精度；(6)根据步骤(5)的评价结果调整GA-ELM算法本身的参数设置，并且不断重复步骤(5)，直到GA-ELM模型的精度达到设定值；(7)通过步骤(6)选择到的GA-ELM模型作为最终模型，我们再为步骤(1)中的四个工艺参数赋值后，通过GA-ELM模型得到相应的晶粒尺寸预测值。本发明的有益效果：与现有技术相比，本发明效果如下：(1)本发明采用最终获得的GA-ELM模型对铝合金压铸件晶粒尺寸预测，能够实现预测的低成本、高效率、高精度；(2)本发明将遗传算法和极限学习机相结合的GA-ELM模型，采用GA对ELM的输入层权值矩阵和隐含层阈值矩阵进行优化，避免了输入层权值矩阵和隐含层阈值矩阵随机性对ELM预测精度的影响，提高了预测准确率和预测效率，成本也大大降低，另外也能够丰富铝合金压铸件晶粒尺寸预测方法的模型库；(3)本发明获得GA-ELM模型是一种高精度、较高效、满足工程要求的模型。其预测精度高于GA-BP模型和原始ELM模型，训练效率高于GA-BP模型，但低于原始ELM模型。附图说明图1是本发明中所述GA-ELM算法流程图；图2是本发明中所述的晶粒尺寸预测流程图；图3是汽车空压机端盖的结构示意图；图4是方框内为汽车空压机端盖接口部位；图5是遗传算法进化结果；图6是GA-ELM模型测试集预测结果对比；图7是GA-ELM模型测试集预测结果误差；图8是GA-BP模型测试集预测结果对比；图9是ELM模型测试集预测结果对比。具体实施方式下面结合附图及具体的实施例对本发明进行进一步介绍。实施例：一种基于GA-ELM算法的铝合金压铸件晶粒尺寸预测方法，该方法包括以下步骤：(1)影响铝合金压铸件晶粒尺寸的压铸工艺参数较多，本方法选取模具预热温度、压射温度、低速充型速度、高速充型速度这四个影响最大的工艺参数作为输入参数；(2)通过软件模拟或实验的方法获得预测的数据样本，将数据样本分为训练集和测试集；(3)使用遗传算法(GA)优化极限学习机(ELM)的初始权值和阈值，从而获得新算法GA-ELM算法；(4)使用步骤(2)中获得的训练集数据样本对步骤(3)中的GA-ELM新算法进行训练，其中作为训练效果评价指标的个体适应度值选为训练集数据样本中最后六组样本数据对应的晶粒尺寸的预测误差平均值；(5)对步骤(4)训练好后的GA-ELM晶粒尺寸预测模型进行测试，将测试样本数据输入到GA-ELM模型中，将GA-ELM模型输出的预测值与测试集的实际值进行对比，评价GA-ELM模型的精度；(6)根据步骤(5)的评价结果调整GA-ELM算法本身的参数设置，并且不断重复步骤(5)，直到GA-ELM模型的精度达到设定值；(7)通过步骤(6)选择到的GA-ELM模型作为最终模型，通过这个模型，我们再为步骤(1)中的四个工艺参数赋值后，无需实验或软件模拟，就可立刻得到相应的晶粒尺寸预测值，大大节约时间及成本。实施例2：ELM基本原理ELM是2006年由南洋理工大学教授HuangGuangBin提出来的一种新型前馈神经网络的学习算法，与传统的单隐层前馈神经网络相比，具有分类准确率高、泛化能力好、调节参数少等优点。ELM神经网络的输入层权值矩阵和隐含层阈值矩阵是随机产生的，并且在之后的运算中无需调整。由理论可知，只需要设置隐含层节点的数量，便可以获得唯一的最优解。对于给定的输入样本，隐含层神经元的输出矩阵的计算公式为H＝g(WXT+b)(1)式中：W为输入层权值矩阵；b为隐含层阈值矩阵；W和b随机产生。神经网络的输出值为P＝(HTβ)(2)式中：β为隐含层到输出层的权值矩阵，只要确定β即可唯一确定ELM神经网络。对于给定的训练输出样本Y，用输出样本替代网络输出值，则权值矩阵β可以根据式(3)求出。其解为：式中：(HT)+为转置矩阵HT的Moore-Penrose广义逆。ELM算法流程如下：(1)确定隐含层神经元个数，随机设定输入层与隐含层间的连接权值ω和隐含层神经元的偏置b；(2)选择一个无限可微的函数作为隐含层神经元的激活函数，进而计算隐含层输出矩阵H；(3)计算输出层权值GA优化ELM模型由以上ELM基本原理可知，其W和b随机产生。在隐含层节点相同的条件下，同一组训练集训练ELM模型，其网络拟合性能会由于W和b的随机产生导致很大差异。遗传算法(GA)具有很强的全局寻优能力，利用GA为ELM模型寻找最优的初始输入层权值矩阵W和隐含层阈值矩阵b，可以提高ELM模型的拟合精度，获取最优ELM模型。GA-ELM训练步骤如下：(1)首先读入实验数据。将实验数据分成训练集和测试集，并将数据进行归一化处理，避免因实验数据数量级相差较大而造成预测误差较大；(2)调用遗传算法(GA)寻找ELM算法最优的初始输入层权值矩阵和隐含层阈值矩阵。种群中的每个个体都包含了一个ELM网络的所有权值和阈值，个体通过适应度函数计算个体适应度值，遗传算法通过选择、交叉和变异操作找到最小适应度值对应个体；个体适应度函数取为ELM网络对训练集中部分样本预测的平均误差；式中yij为训练集中部分样本的输出预测值，xij为训练集部分样本真值，N为训练集部分样本个数；(3)用遗传算法得到的最优个体对ELM的初始权值和阈值赋值，并设置隐含层节点个数，完成GA-ELM模型建立；④利用测试集样本对GA-ELM模型进行测试及效果评价。训练集样本数据的获取首先，选取与凝固过程密切相关的压铸工艺参数作为输入参数，输入参数选定为模具预热温度、压射温度、低速充型速度、高速充型速度四个参数；然后，因为压铸件不同位置晶粒尺寸不相同，所以我们选取铸件上对机械性能要求较高的部位的晶粒尺寸最大值作为输出参数；最后，通过压铸模拟软件Anycasting对不同的输入参数值进行模拟实验，获得具体的输出参数值。以汽车空压机端盖的压铸成型为例，其几何模型如图3所示，轮廓尺寸112mm×112mm×84mm,平均壁厚5mm，材料为铝合金ADC12，汽车空压机端盖接口处如图4，此部位要求常温下力学性能优良，晶粒尺寸细小，因此我们选取该部位晶粒尺寸最大值(以下简称晶粒尺寸)作为模拟实验的输出参数，同时根据压铸生产经验确定模拟实验的输入参数值及水平设置，如表1所示。表1各成型工艺参数值及水平设置采用四因素四水平正交试验法对该铸件的压铸工艺方案进行优化设计,即L32(45)正交表,共32组实验。用Anycasting仿真模拟软件对这32种工艺方案进行模拟，获得不同工艺参数条件下的晶粒尺寸值，这32组样本作为训练集，工艺参数的正交试验表及模拟结果如表2所示。表2训练集工艺参数模拟结果遗传算法优化中的个体适应度值取为训练集中序号27—32共6个样本的预测平均误差值。2.2GA-ELM参数设置利用表2中的训练集样本数据对GA-ELM算法模型进行训练。GA-ELM模型完整地保留了GA和ELM算法中的可调参数，这些参数的选取可以参考ELM和GA算法的相关文献。本文通过多次调整相关参数，将得到的最终的实验结果进行对比，给出效果最好的一组推荐值，如表3所示。表3GA-ELM参数设置表序号参数设置1ELM隐含层节点数322种群规模603最大迭代次数1504交叉概率0.85变异概率0.56目标函数平均相对误差最小7适应度评估方式线性评估8权值wij取值范围[-1,1]9阈值bi取值范围[-1,1]10终止条件满足最大迭代次数2.3测试集样本数据的获取测试集样本数据工艺参数的选取如表4所示，同样运用anycasting软件模拟实验结果。表4测试集工艺参数模拟2.4预测效果及分析遗传算法优化的进化结果如图5所示,图5内容为个体适应度值变化曲线。从图5可以看出遗传算法部分收敛的很好，在30代时已基本收敛至最优权值和阈值。由于其权值矩阵和阈值矩阵规模较大，其具体取值不再赘述。我们利用建立完成的GA-ELM模型对测试集数据进行预测，并与测试集输出真值进行对比，如图6所示。为了更加直观的反映GA-ELM模型对测试集数据的预测效果，我们将预测值与真值的绝对误差以图形的形式给出，如图7所示。由图7我们看到，除第四组样本外，其他测试集样本误差均控制在10μm以内，第四组样本误差也不超过22μm，考虑到研究内容为微观尺寸下的晶粒，微观尺寸内存在一定的扰动因素，并且训练使用的样本数量较少，拟合度有限，因此不超过22μm的最大误差属于可以接受的最大误差值。同时，通过计算，测试集样本数据预测平均绝对误差为10.2μm,平均相对误差为3.8％。该方法可以准确、有效地对晶粒尺寸进行预测。2.5与其他模型预测结果对比为了体现该模型的优越性，采用GA-BP神经网络及原始ELM模型对该样本进行预测，其中原始ELM模型隐含层节点数为60(多次试验确定)，隐含层激励函数选择“sigmoid”函数；GA-BP神经网络模型隐含层节点数设为25(多次试验确定)，隐含层激励函数选择“logsig”函数。GA-BP神经网络模型及原始ELM模型的预测结果如图8、图9。以上三种模型的预测结果对比情况见表5。表5三种预测模型预测性能对比模型指标GA-ELMGA-BPELM平均绝对误差/μm10.214.422.8平均相对误差/％3.85.58.6训练时间/s47.03107.022.23由表5可以看出，GA-ELM模型在预测精度上要明显优于其他两个模型。但由于采用了遗传算法，GA-ELM模型的训练效率要远低于原始ELM模型。但是，即使如此，GA-ELM模型的训练效率也要远高于GA-BP模型，其效率较高，GA-ELM模型具有较高的预测精度，可以相对准确地预测铝合金压铸件晶粒尺寸。本发明提出了一种将遗传算法和极限学习机相结合的GA-ELM模型，采用GA对ELM的输入层权值矩阵和隐含层阈值矩阵进行优化，避免了输入层权值矩阵和隐含层阈值矩阵随机性对ELM预测精度的影响，提高了预测准确率。丰富了铝合金压铸件晶粒尺寸预测方法的模型库。本发明的GA-ELM模型是一种高精度、较高效、满足工程要求的模型。其预测精度高于GA-BP模型和原始ELM模型，训练效率高于GA-BP模型，但低于原始ELM模型。以上所述，仅为本发明的具体实施方式，但本发明的保护范围并不局限于此，任何熟悉本
技术领域：
的技术人员在本发明揭露的技术范围内，可轻易想到变化或替换，都应涵盖在本发明的保护范围之内，因此，本发明的保护范围应以所述权利要求的保护范围为准。当前第1页1 2 3