一种双吊钩吊装系统的安全性计算方法和计算装置与流程

本发明涉及吊装对象的吊装系统安全性计算领域，尤其是涉及一种双吊钩吊装系统的安全性计算方法和计算装置。

背景技术：

随着重型吊装对象的大型化，吊装对象的吨位越来越大，用单台起重机吊装往往满足不了作业需求，为了保证吊装过程的安全性、平稳性，双机或多机协同作业日益增多。在常见的双机吊装作业中，吊装绳负载变形，吊钩发生转动，均可对吊装系统安全性产生不利影响。

目前已存在一些对大型吊装对象吊装的技术发明。例如，申请号为CN201410713436.5的专利文献提供了一种起重机吊装动作规划方法，针对现存的高维动作规划方法在起重机吊装动作规划中因所得路径迂回严重、平滑性较差而导致的路径代价大、规划时间长、路径质量差的问题。首先通过定义吊装系统位形对吊装动作规划问题进行建模，然后对起重机的运动进行非完整性运动学分析建立起重机的运动学模型，最后采用一种启发式采样策略，提高决定RRT数生长方向的随机采样点的质量，引导随机树向能够生成较短路径的方向扩展。本发明规划出一条从起始位置到就位位置的安全的、可行的、没有碰撞的、高质量的动作序列，使随机树生长具有一定的方向性，有效地缓解了路径迂回，使最终路径更平滑，从而降低路径代价，有效地避免不必要的碰撞，收敛速度快，能较快找到一条相对平滑的从初始点到目标点的路径，大大节省了规划时间。

申请号为CN201210358707.0的专利文献提供了一种基于运动学和动力学的双移动式起重机协同吊装仿真方法，在由主起重机、辅助起重机、被吊吊装对象及吊索具构成的双机系统中，采用运动学和动力学建立双机协同吊装的仿真模型，双机系统中的部件运动分为运动学和动力学两部分。将双机系统划分成三部分，被吊装对象、与吊索具作为一部分，称为双机的起升子系统；主起重机为一部分，称为主起重机子系统；辅助起重机为一部分，称为辅助起重机子系统；其中，双机的起升子系统采用动力学建模，而主起重机子系统和辅助起重机子系统采用运动学建模。该发明提供的一种基于运动学、动力学的混合双机吊装仿真模型的建立，是通过对吊装系统分别进行运动学建模和动力学建模。由于对起重机模型运用动力学建模时会很复杂，并考虑了起重机结构的惯性矩和各部件之间的作用力和力矩，而实际在仿真过程中是没有必要考虑这些参数，因此会增加建模的难度，采用运动学建模就可避免这种问题，简化建模过程，提高了效率，同时不会对仿真效果产生影响，对于双机起升机构则采用了动力学建模，这样可以仿真出起升绳的摇摆动作，相对运动学建模更准确。

再例如，申请号为CN201310152926.8的专利文献提供了一种双台起重机协同作业载荷分配优化方法，计算双台汽车起重机吊装过程中载荷的分配并进行载荷分配优化，制定吊装作业方案，指导实际吊装，进一步降低双机协同吊装风险。该发明所采用的技术方案是：一种双台起重机协同作业载荷分配优化方法，该方法为：1)三维场景建模：提供多机型起重机数据，以模型数据文件的形式建立起重机模型库；2)起重机选型：用户根据工况从起重机模型库中选择符合吊装要求的主起重机和辅起重机；3)起重机配置：根据负载能力、起升高度的吊装作业要求配置两台起重机伸缩臂的伸缩比、配重；4)双台起重机协同吊装动作计算：应用逆运动学原理，根据吊装对象的期望运动，即双机起升、双机翻转、双机旋转，确定两台起重机的协同动作序列；5)双台起重机协同吊装参数计算：根据静力学原理计算两台起重机在双机起升、双机翻转、双机旋转时的载荷；6)双台起重机协同吊装载荷分配优化计算：根据双台起重机的参数信息和吊装物的重量进行双台起重机载荷分配优化计算；7)设定吊装目标点，通过键盘操作来实现吊装模拟操作，判断吊装物是否达到所设置的吊装目标点；若是，进入8)；若否，返回4)；8)结束吊装过程。该发明分析了影响额定起重量的影响因素，研究了协同作业过程各起重机实时载荷模型，发明了一种载荷分配优化的方法。

申请号为CN 201410201903.6的专利文献提供了一种模拟大型吊装对象吊装过程的方法和装置，基于CAM平台，提出了一种模拟吊装对象吊装的计算机模拟方法，方法包括：在CAM平台上创建三维吊装模型，三维吊装模型中各组件为运动副装配关系；根据预先拟定的吊装方案按实际尺寸计算三维吊装模型中主吊车和溜尾吊车的运动参数及吊装对象重心，并根据运动参数及吊装对象重心在CAM平台上模拟大型吊装对象的吊装过程；获取吊装过程中大型吊装对象的模拟吊装位置，将大型吊装对象的模拟吊装位置与预先拟定的吊装方案中的预设吊装位置进行比较，根据比较结果对大型吊装对象进行吊装。该发明通过在CAM平台上创建三维吊装模型，并将创建的三维吊装模型中的各组件进行运动副装配，进而模拟大型吊装对象的吊装过程，从而提高了模拟的精度。

申请号为CN 201510437238.5的专利文献提供了一种大型吊装对象吊装的吊索具及吊装方法，用于解决大型吊装对象吊装时设置八个吊耳，从而导致八个分支吊索的长度调整耗费时间长、难度大、容易引起吊装对象变形的问题。为解决上述技术问题，该发明的技术方案如下：一种大型吊装对象吊装的吊索具，包括设置于吊装对象底座上的若干吊装组件，若干吊装组件依次横跨固定于吊装对象上，吊装组件包括主吊索、横向支撑以及分支吊索，横向支撑通过主吊索悬设于吊装对象上方，若干分支吊索分设于吊装对象底座的两侧，分支吊索的两端分别与吊装对象底座固定连接。该发明解决了大型吊装对象吊装时分支吊索的长度调整耗费时间长、难度大、易引起吊装对象变形的问题。

但是以上所有的吊装计算、模拟技术均存在以下不足：

(1)未考虑吊装系统的弹性变形；

(2)未考虑吊装系统在重力作用下发生的转动，尤其是吊钩的转动效应；

(3)未涉及吊装系统安全性指标计算，如计算吊装系统的稳定安全距离、干涉检查等。

技术实现要素：

为了解决上述问题，本发明的目的在于提供一种双吊钩吊装系统的安全性计算方法，包括以下步骤：有限元建模，建立由吊装对象、吊钩、吊装绳组成的吊装系统的有限元模型，在有限元模型中施加吊装系统的重力载荷；施加位移约束，在有限元模型的吊钩上添加多个弹性杆，每个弹性杆的一端与吊钩相连接，在其另一端上施加三个方向的位移约束，同时在有限元模型的吊装对象上选择或者添加多个附加约束点，在多个附加约束点上分别施加位移约束，弹性杆上和附加约束点上的位移约束共同实现有限元模型的完全约束或者过度约束状态；设定参数值和收敛准则，设定各个位移约束的参数值和收敛准则；初始支反力计算，根据有限元模型和参数值，计算各个位移约束对应的初始支反力；收敛判断，对各个初始支反力进行判断，当各个初始支反力均满足收敛准则时，得到收敛稳定状态的有限元模型；否则对各个位移约束进行迭代计算，直到各个位移约束对应的支反力均满足收敛准则。

优选地，参数值包括位移约束的初始位移值初始位移增量可变位移约束个数m和最大迭代次数n，其中，j＝1，…，m，i＝1，…，n；m和n均为正整数。

进一步地，迭代计算包括以下步骤：标记当前组，依照对有限元模型的不同自由度的限制，对其中可变的各个位移约束进行分组并根据有限元模型和参数值，计算各个位移约束对应的支反力，找出各个组中的位移约束对应的支反力的绝对值的和最大的一组，将其标记为当前组；标记当前位移约束，在当前组的位移约束中找出对应的支反力的绝对值最大的位移约束，将其标记为当前位移约束；当前支反力计算，根据割线迭代法求解当前位移约束的位移值，根据当前位移约束的位移值重新计算各个位移约束对应的支反力；迭代收敛判断，当重新计算得到的各个支反力均满足收敛准则时，得到收敛稳定状态的有限元模型；否则重复进行当前约束调整计算，直到各个位移约束对应的支反力均满足收敛准则。

优选地，当前约束调整计算包括以下步骤：当前组判断，对当前组中的位移约束进行判断，当当前组中的位移约束对应的支反力均满足收敛准则时，则进行步骤标记当前组～迭代收敛判断；当存在当前组中的位移约束对应的支反力不满足收敛准则时，则进行步骤标记当前约束～迭代收敛判断。

进一步地，割线迭代法采用以下公式：

其中，为设定的当前位移约束的初始位移值，为设定的当前位移约束的首次位移增量，m为可变位移约束个数，n为设定的最大迭代次数，为根据公式进行第i次迭代求解得到的当前位移约束的位移值，为根据进行第i次计算得出的当前位移约束的支反力，m和n均为正整数。

优选地，收敛准则为：各个位移约束对应的支反力的绝对值均小于设定的收敛阈值。

进一步地，当有限元模型达到收敛稳定状态之后，还包括以下步骤中的任意一项或多项：对双吊钩吊装系统的稳定安全距离进行计算；对双吊钩吊装系统中的一个位置和吊装绳进行干涉判断；对双吊钩吊装系统的位置姿态进行计算；在有限元模型中提取吊装绳负载和吊钩负载。

优选地，对双吊钩吊装系统的稳定安全距离进行计算具体包括：在有限元模型中提取吊装对象的重心点和吊耳点的坐标；根据坐标将重心点和多个吊耳点投影到同一水平面上，多个吊耳点的投影点形成一个多边形，计算重心点的投影点到多边形各边的最小距离，即为双吊钩吊装系统的稳定安全距离。

进一步地，对双吊钩吊装系统中的一个位置和吊装绳进行干涉判断具体包括；根据需要指定双吊钩吊装系统中的一个位置，该一个位置为一个点或者一条线段；在有限元模型中提取一个点或者一条线段两端点的坐标，并提取一个吊装绳的两端点坐标，根据吊装绳的两端点坐标得到该吊装绳的两端点连线；根据一个点或者一条线段两端点的坐标和吊装绳的两端点连线，计算一个位置到两端点连线的最小距离，根据最小距离判断一个位置和吊装绳的干涉状态。

优选地，对双吊钩吊装系统的位置姿态进行计算具体包括：根据需要指定吊装对象和吊钩上的两个位置点；在有限元模型中分别提取两个位置点的坐标；基于两个位置点的坐标，根据空间几何学原理计算双吊钩吊装系统的位置姿态。

本发明还提供一种双吊钩吊装系统的安全性计算装置，包括以下模块：有限元建模模块，用于建立由吊装对象、吊钩、吊装绳组成的吊装系统的有限元模型，在有限元模型中施加吊装系统的重力载荷；位移约束施加模块，用于在有限元模型的吊钩上添加多个弹性杆，每个弹性杆的一端与吊钩相连接，在其另一端上施加位移约束，同时在有限元模型的吊装对象上选择或者添加多个附加约束点，在多个附加约束点上分别施加位移约束，弹性杆上和附加约束点上的位移约束共同实现有限元模型的完全约束或者过度约束状态；参数设定模块，用于设定各个位移约束的参数值和收敛准则；初始支反力计算模块，用于根据有限元模型和参数值，计算各个位移约束对应的初始支反力；初始收敛判断模块，用于对各个初始支反力进行判断，当各个初始支反力均满足收敛准则时，得到收敛稳定状态的有限元模型；否则对各个位移约束进行迭代计算，直到各个位移约束对应的支反力均满足收敛准则。

优选地，参数值包括位移约束的初始位移值初始位移增量可变位移约束个数m和最大迭代次数n，其中，j＝1，…，m，i＝1，…，n；m和n均为正整数。

进一步地，迭代计算是利用以下迭代计算模块进行的：当前组标记模块，用于依照对有限元模型的不同自由度的限制，对其中可变的各个位移约束进行分组，并根据有限元模型和参数值，计算各个位移约束对应的支反力，找出各个组中的位移约束对应的支反力的绝对值的和最大的一组，将其标记为当前组；当前位移约束标记模块，用于在当前组的位移约束中找出对应的支反力的绝对值最大的位移约束，将其标记为当前位移约束；当前支反力计算模块，用于根据割线迭代法求解当前位移约束的位移值，根据当前位移约束的位移值重新计算各个位移约束对应的支反力；迭代收敛判断模块，用于当重新计算得到的各个支反力均满足收敛准则时，得到收敛稳定状态的有限元模型；否则重复进行当前约束调整计算，直到各个位移约束对应的支反力均满足收敛准则。

优选地，当前约束调整计算是利用以下模块进行的：当前组判断模块，用于对当前组中的位移约束进行判断，当当前组中的位移约束对应的支反力均满足收敛准则时，则进行步骤标记当前组～迭代收敛判断；当前约束判断模块，用于当存在当前组中的位移约束对应的支反力不满足收敛准则时，则进行步骤标记当前约束～迭代收敛判断，直到各个位移约束对应的支反力均满足收敛准则。

进一步地，割线迭代法采用以下公式：

其中，为设定的当前位移约束的初始位移值，为设定的当前位移约束的首次位移增量，m为可变位移约束个数，n为设定的最大迭代次数，为根据公式进行第i次迭代求解得到的当前位移约束的位移值，为根据进行第i次计算得出的当前位移约束的支反力，m和n为正整数。

优选地，收敛准则为：各个位移约束对应的支反力的绝对值均小于设定的收敛阈值。

进一步地，当有限元模型达到收敛稳定状态之后，还可运行以下模块中的任意一个或多个：安全距离计算模块，用于对双吊钩吊装系统的稳定安全距离进行计算；干涉判断模块，用于对双吊钩吊装系统中的一个位置和吊装绳进行干涉判断；位置姿态计算模块，用于对双吊钩吊装系统的位置姿态进行计算；提取模块，用于在有限元模型中提取吊装绳负载和吊钩负载。

优选地，安全距离计算模块包括：第一坐标提取模块，用于在有限元模型中提取吊装对象的重心点和吊耳点的坐标；投影计算模块，用于根据坐标将重心点和多个吊耳点投影到同一水平面上，多个吊耳点的投影点形成一个多边形，计算重心点的投影点到多边形各边的最小距离，即为双吊钩吊装系统的稳定安全距离。

进一步地，干涉判断模块包括；第一位置点提取模块，用于根据需要指定双吊钩吊装系统中的一个位置，该一个位置为一个点或者一条线段；第二坐标提取模块，用于在有限元模型中提取一个点或者一条线段两端点的坐标，并提取一个吊装绳的两端点坐标，根据吊装绳的两端点坐标得到该吊装绳的两端点连线；距离计算模块，用于根据一个点或者一条线段的两端点的坐标和吊装绳的两端点连线，计算一个位置到两端点连线的最小距离，根据最小距离判断一个位置和吊装绳的干涉状态。

优选地，位置姿态计算模块包括：第二位置点提取模块，用于根据需要指定吊装对象和吊钩上的两个位置点；第三坐标提取模块，用于在有限元模型中分别提取两个位置点的坐标；几何计算模块，用于基于两个位置点的坐标，根据空间几何学原理计算双吊钩吊装系统的位置姿态。

如上，利用本发明的双吊钩吊装系统安全性的计算方法和双吊钩吊装系统安全性的计算装置，实现欠约束的双吊钩吊装系统在重力作用下的静力学计算，可计算吊装对象、吊钩和吊装绳的最终收敛稳定状态，并根据最终状态，计算双吊钩吊装系统的稳定安全距离、指定位置与吊载绳最小距离、吊装对象倾斜状态、吊钩位置姿态、吊装绳负载和吊钩负载，可指导吊装工艺准确地制定，从而降低双钩协同吊装的风险。

为让本发明的上述内容能更明显易懂，下文特举优选实施例，并结合附图，作详细说明如下。

附图说明

图1为本发明的第一实施例和第二实施例中的双吊钩吊装系统的安全性计算方法流程图；

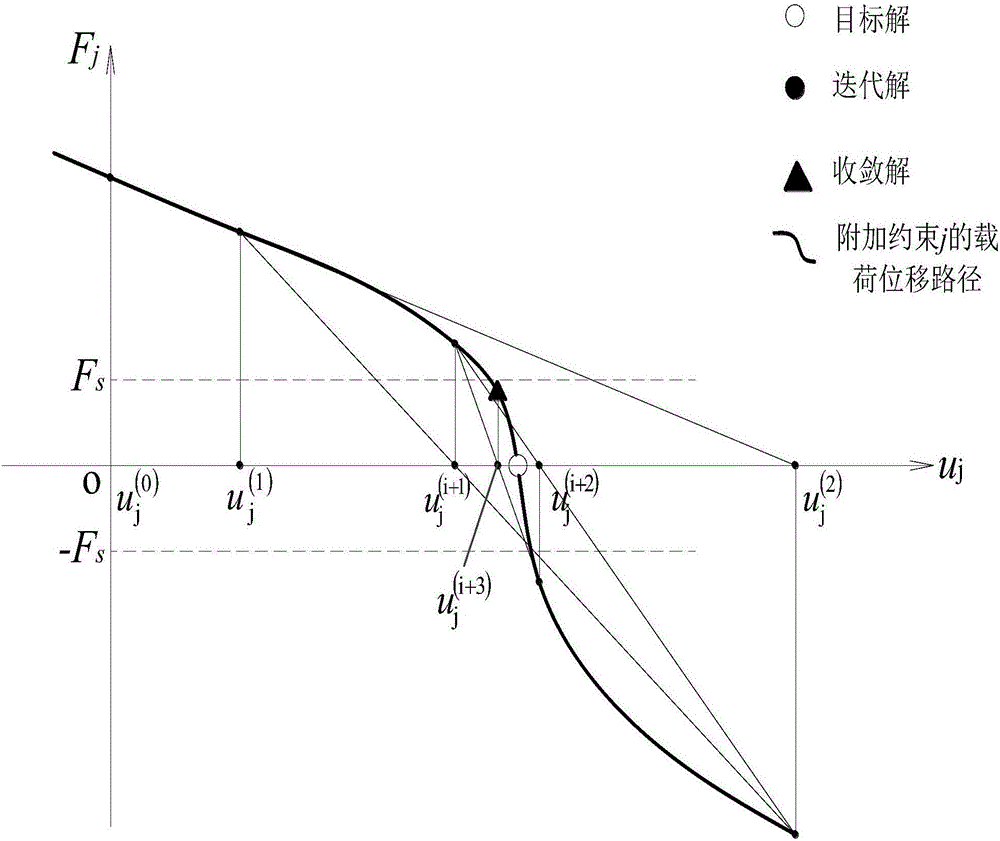
图2为本发明第二实施例中的割线迭代法的方程曲线；

图3为本发明第三实施例中的大梁组件安装示意图；

图4为本发明第三实施例中的最终稳定吊装系统在水平面上的投影示意图，

图5为本发明第四实施例双吊钩吊装系统的安全性计算装置的模块连接示意图。

具体实施方式

以下由特定的具体实施例说明本发明的实施方式，本领域技术人员可由本说明书所揭示的内容轻易地了解本发明的其他优点及功效。虽然本发明的描述将结合较佳实施例一起介绍，但这并不代表此发明的特征仅限于该实施方式。恰恰相反，结合实施方式作发明介绍的目的是为了覆盖基于本发明的权利要求而有可能延伸出的其它选择或改造。为了提供对本发明的深度了解，以下描述中将包含许多具体的细节。本发明也可以不使用这些细节实施。此外，为了避免混乱或模糊本发明的重点，有些具体细节将在描述中被省略。

另外，在以下的说明中所使用的“上”、“下”、“左”、“右”、“顶”、“底”，不应理解为对本发明的限制。

【第一实施例】

如图1中所示，本发明第一实施例公开了一种双吊钩吊装系统的安全性计算方法，包括以下步骤：

步骤S11，有限元建模，建立由吊装对象、吊钩、吊装绳组成的吊装系统的有限元模型，在有限元模型中施加吊装系统的重力载荷；

步骤S12，施加位移约束，在有限元模型的吊钩上添加多个弹性杆，每个弹性杆的一端与吊钩相连接，在其另一端上施加位移约束，同时在有限元模型的吊装对象上选择或者添加多个附加约束点，在多个附加约束点上分别施加位移约束，弹性杆上和附加约束点上的位移约束共同实现有限元模型的完全约束或者过度约束状态；

步骤S13，设定参数值和收敛准则，设定各个位移约束的参数值和收敛准则；

步骤S14，初始支反力计算，根根据有限元模型和参数值，计算各个位移约束对应的初始支反力；

步骤S15，收敛判断，对各个初始支反力进行判断，当各个初始支反力均满足收敛准则时，得到收敛稳定状态的有限元模型；否则对各个位移约束进行迭代计算，直到各个位移约束对应的支反力均满足收敛准则。

更为具体地，在步骤S12中添加附加约束点的目的是使吊钩和吊装对象在重力作用下静力稳定，即使得吊钩和吊装对象的六个自由度(3个平动+3个转动)处于满约束或过约束状态。在吊钩上添加若干弹性杆，该弹性杆是仅可承受轴向拉压的附加约束杆，弹性杆的一端与吊钩连接，另一端施加3个方向的位移约束，约束位移值可全为零，并且其中2个方向始终保持零位移约束。在吊装对象上选择或添加可以随着吊装对象运动的若干点，作为附加约束点，在这些约束点上施加位移约束，约束位移值可全为零，保证吊装对象静力稳定条件下，尽可能少地添加位移约束。

其中，有限元建模步骤中，可以应用有限元软件建立由吊装对象、吊钩和吊装绳组成的吊装系统的有限元模型，有限元软件可以应用ANSYS，Patran/Nastran，Abaqus，Hypermesh，吊装对象是指被吊装的设备、装置等。上述的完全约束或者过约束状态，是指实现该有限元模型的一种静定状态，一般而言，在完全约束状态下的机械系统处于静定状态，在这样的静定状态下，撤销位移约束或不适当的更改位移约束可以使机械系统变成可变体系，即欠约束状态，而增加位移约束又使其变成有多余位移约束的不变体系，即过度约束状态。其中，上述的收敛准则是指使得上述有限元模型能够达到安全收敛稳定状态的条件，即当上述有限元模型满足该收敛准则时，即认为该有限元模型达到收敛稳定状态。

更进一步地，上述的参数值包括位移约束的初始位移值初始位移增量可变位移约束个数m和最大迭代次数n，其中，j＝1，…，m，i＝0，1，…，n；m和n均为正整数。

优选地，可将收敛准则设定为：各个位移约束对应的支反力的绝对值均小于设定的收敛阈值，用F_s表示该设定的收敛阈值，可将该收敛准则设定为即判断各个位移约束的初始支反力或当前位移约束支反力的绝对值是否小于F_s，若均小于，则满足收敛准则。需要注意的是，本发明并不限于本实施例所提供的收敛准则，还可以采用其他能够使得上述有限元模型达到安全收敛稳定状态的设定条件来作为收敛准则。

优选地，当有限元模型达到收敛稳定状态之后，还可进行以下后处理步骤中的任意一项或多项：对双吊钩吊装系统的稳定安全距离进行计算；对双吊钩吊装系统中的一个位置和吊装绳进行干涉判断；对双吊钩吊装系统的位置姿态进行计算；在有限元模型中提取吊装绳的轴向力；在有限元模型中提取吊钩上端约束的支反力；在有限元模型中提取吊装绳负载和吊钩负载。

进一步地，对双吊钩吊装系统的稳定安全距离进行计算具体包括：在有限元模型中提取吊装对象的重心点和吊耳点的坐标；根据坐标将重心点和多个吊耳点投影到同一水平面上，多个吊耳点的投影点形成一个多边形，计算重心点的投影点到多边形各边的最小距离，即为双吊钩吊装系统的稳定安全距离。

优选地，对双吊钩吊装系统中的一个位置和吊装绳进行干涉判断具体包括；根据需要指定双吊钩吊装系统中的一个位置，该一个位置为一个点或者一条线段；在有限元模型中提取一个点或者一条线段两端点的坐标，并提取一个吊装绳的两端点坐标，根据吊装绳的两端点坐标得到该吊装绳的两端点连线；根据一个点或者一条线段的两端点的坐标和吊装绳的两端点连线，计算一个位置到两端点连线的最小距离，根据最小距离判断一个位置和吊装绳的干涉状态。

进一步地，对双吊钩吊装系统的位置姿态进行计算具体包括：根据需要指定吊装对象和吊钩上的两个位置点；在有限元模型中分别提取两个位置点的坐标；基于两个位置点的坐标，根据空间几何学原理计算双吊钩吊装系统的位置姿态。

【第二实施例】

如图1中所示，本发明第二实施例公开了一种双吊钩吊装系统的安全性计算方法，包括以下步骤：

步骤S11，有限元建模，建立由吊装对象、吊钩、吊装绳组成的吊装系统的有限元模型，在有限元模型中施加吊装系统的重力载荷；

步骤S12，施加位移约束，在有限元模型的吊钩上添加多个弹性杆，每个弹性杆的一端与吊钩相连接，在其另一端上施加位移约束，同时在有限元模型的吊装对象上选择或者添加多个附加约束点，在多个附加约束点上分别施加位移约束，弹性杆上和附加约束点上的位移约束共同实现有限元模型的完全约束或者过度约束状态；

步骤S13，设定参数值和收敛准则，设定各个位移约束的参数值和收敛准则；

步骤S14，初始支反力计算，根根据有限元模型和参数值，计算各个位移约束对应的初始支反力；

步骤S15，初始收敛判断，对各个初始支反力进行判断，当各个初始支反力均满足收敛准则时，得到收敛稳定状态的有限元模型；否则对各个位移约束进行迭代计算，直到各个位移约束对应的支反力均满足收敛准则。

进一步地，迭代计算具体包括以下步骤：

步骤S16，标记当前组，依照对有限元模型的不同自由度的限制，对其中可变的各个位移约束进行分组,并根据有限元模型和参数值，计算各个位移约束对应的支反力，找出各个组中的位移约束对应的支反力的绝对值的和最大的一组，将其标记为当前组；

步骤S17，标记当前位移约束，在当前组的位移约束中找出对应的支反力的绝对值最大的位移约束，将其标记为当前位移约束；

步骤S18，当前支反力计算，根据割线迭代法求解当前位移约束的位移值，根据当前位移约束的位移值重新计算各个位移约束对应的支反力；

步骤S19，迭代收敛判断，当重新计算得到的各个支反力均满足收敛准则时，得到收敛稳定状态的有限元模型；否则重复进行当前约束调整计算，直到各个位移约束对应的支反力均满足收敛准则。

优选地，当前约束调整计算具体包括以下步骤：

步骤S20，当前组判断，对当前组中的位移约束进行判断，当当前组中的位移约束对应的支反力均满足收敛准则时，则进行步骤标记当前组～迭代收敛判断；当存在当前组中的位移约束对应的支反力不满足收敛准则时，则进行步骤标记当前约束～迭代收敛判断。

进一步地，割线迭代法采用以下公式：

其中，为设定的当前位移约束的初始位移值，为设定的当前位移约束的首次位移增量，m为可变位移约束个数，n为设定的最大迭代次数，为根据公式进行第i次迭代求解得到的当前位移约束的位移值，为根据在有限元模型中进行第i次计算得出的当前位移约束的支反力，m和n为正整数。

优选地，可将收敛准则设定为：各个位移约束对应的支反力的绝对值均小于设定的收敛阈值，用F_s表示该设定的收敛阈值，可将该收敛准则设定为即判断各个位移约束的初始支反力或当前位移约束支反力的绝对值是否小于F_s，若均小于，则满足收敛准则。需要注意的是，本发明并不限于本实施例所提供的收敛准则，还可以采用其他能够使得上述有限元模型达到安全收敛稳定状态的设定条件来作为收敛准则。

更为具体地，在步骤S12中添加附加约束点的目的是使吊钩和吊装对象在重力作用下静力稳定，即使得吊钩和吊装对象的六个自由度(3个平动+3个转动)处于满约束或过约束状态。在吊钩上添加若干弹性杆，该弹性杆是仅可承受轴向拉压的附加约束杆，在弹性杆的一端与吊钩联结，另一端施加3个方向的位移约束，约束位移值可全为零，并且其中2个方向始终保持零位移约束。在吊装对象上选择或添加可以随着吊装对象运动的若干点，作为附加约束点，在这些约束点上施加位移约束，约束位移值可全为零，保证吊装对象静力稳定条件下，尽可能少地添加位移约束。

其中，有限元建模步骤中，可以应用有限元软件建立由吊装对象、吊钩和吊装绳组成的吊装系统的有限元模型，有限元软件可以应用ANSYS，Patran/Nastran，Abaqus，Hypermesh，吊装对象是指被吊装的设备、装置等。上述的完全约束或者过约束状态，是指实现该有限元模型的一种静定状态，一般而言，在完全约束状态下的机械系统处于静定状态，在这样的静定状态下，撤销位移约束或不适当的更改位移约束可以使机械系统变成可变体系，即欠约束状态，而增加位移约束又使其变成有多余位移约束的不变体系，即过度约束状态。其中，上述的收敛准则是指使得上述有限元模型能够达到安全收敛稳定状态的条件，即当上述有限元模型满足该收敛准则时，即认为该有限元模型达到收敛稳定状态。

优选地，当有限元模型达到收敛稳定状态之后，还可进行以下后处理步骤中的任意一项或多项：对双吊钩吊装系统的稳定安全距离进行计算；对双吊钩吊装系统中的一个位置和吊装绳进行干涉判断；对双吊钩吊装系统的位置姿态进行计算；在有限元模型中提取吊装绳的轴向力；在有限元模型中提取吊钩上端约束的支反力；在有限元模型中提取吊装绳负载和吊钩负载。

进一步地，对双吊钩吊装系统的稳定安全距离进行计算具体包括：在有限元模型中提取吊装对象的重心点和吊耳点的坐标；根据坐标将重心点和多个吊耳点投影到同一水平面上，多吊耳点的投影点形成一个多边形，计算重心点的投影点到多边形各边的最小距离，即为双吊钩吊装系统的稳定安全距离。

优选地，对双吊钩吊装系统中的一个位置和吊装绳进行干涉判断具体包括；根据需要指定双吊钩吊装系统中的一个位置，该一个位置为一个点或者一条线段；在有限元模型中提取一个点或者一条线段的两端点的坐标，并提取一个吊装绳的两端点坐标，根据吊装绳的两端点坐标得到该吊装绳的两端点连线；根据一个点或者一条线段的两端点的坐标和两端点连线，计算一个位置到两端点连线的最小距离，根据最小距离判断一个位置和吊装绳的干涉状态。

进一步地，对双吊钩吊装系统的位置姿态进行计算具体包括：根据需要指定吊装对象和吊钩上的两个位置点；在有限元模型中分别提取两个位置点的坐标；基于两个位置点的坐标，根据空间几何学原理计算双吊钩吊装系统的位置姿态。

【第三实施例】

本实施例以采用双吊钩带水平绳方式进行吊装的某岸桥大梁组件的安装为例来对本发明第二实施例的方法进行详细说明：

如图3中所示，作为吊装对象的该大梁组件301重量为855吨，两吊钩302a和302b之间的水平距离为15000mm。按图3来定义各位置点名称和载荷约束变量，长度单位为mm。在重力作用变形前，大梁组件301重心G坐标为(16849，72740，182)，吊耳点E、F、J、K坐标分别为(1075，59570，-3474)、(1075，59570，3474)、(30600，59570，-3400)、(30600，59570，3400)，吊钩点A、B、C、D坐标分别为(7600，83871，-550)、(7600，83871，550)、(22600，84577，-550)、(22600，84577，550)。

首先在有限元软件中建立由大梁组件301、吊钩302和吊装绳303组成吊装系统的有限元模型，根据实际情况在该有限元模型中施加重力载荷。

其次按照图3所示来施加位移约束，在吊钩处添加4根刚度很小的弹性杆以形成柔性约束，该弹性杆的截面积100mm²，长度4m，使吊钩可稳定转动。在大梁组件301上选取四个点，分别记为M，N，P，Q，按图3施加附加位移约束，使大梁组件301达到完全约束或者过度约束的状态。

接着按照下表1来设定各个参数初始值：

表1

在有限元软件中运行本发明算法，即按照以下步骤进行：

根据有限元模型和表1中设定的参数值，计算各个位移约束对应的初始支反力，并对各个初始支反力进行判断，当各个初始支反力的绝对值均小于收敛阈值时，各个位移约束对应的支反力满足收敛准则。本发明第三实施例中，计算得到的初始支反力中存在绝对值不小于设定的收敛阈值F_s的情形，则对各个位移约束进行迭代计算，直到各个位移约束对应的支反力均满足收敛准则。

进一步地，迭代计算包括以下步骤：

位移约束分组，依照对有限元模型的不同自由度的限制，对其中可变的各个位移约束进行分组，更为具体地，本实施例中的位移约束分组方法为：如图3中所示，附加约束对吊钩和大梁组件的自由度限制作用，使吊钩和大梁组件达到满约束或过约束的静力稳定状态。约定：UX表示X方向的平动自由度，RX表示绕X方向的转动自由度，Y和Z方向自由度采用相同方法表示。

Or吊钩：(UX,UY,UZ在Or处被约束)

O_f吊钩：(UX,UY,UZ在O_f处被约束)

大梁组件：(UY被吊绳约束)

则附加约束分组如下：

约束组1：u₁、u₂

约束组2：u₃、u₄

约束组3：u₅

约束组4：u₆、u₇

约束组5：u₈、u₉

标记当前组，根据有限元模型和参数值，计算各个位移约束对应的支反力，找出各个组中的位移约束对应的支反力的绝对值的和最大的一组，将其标记为当前组。例如计算得到的位移约束对应的支反力中，约束组1的两个位移约束对应的支反力的绝对值为最大，则将约束组1标记为当前组。

标记当前位移约束，在当前组的位移约束中找出对应的支反力的绝对值最大的位移约束，将其标记为当前位移约束。例如在上述约束组1中，u₁的绝对值大于u₂，则将u₁标记为当前位移约束。

当前支反力计算，根据割线迭代法求解当前位移约束的位移值，根据当前位移约束的位移值重新计算各个位移约束对应的支反力。割线迭代法采用以下公式：

其中，为设定的当前位移约束的初始位移值，为设定的当前位移约束的首次位移增量，m为可变位移约束个数，n为设定的最大迭代次数，为根据公式进行第i次迭代求解得到的当前位移约束的位移值，为根据在有限元模型中进行第i次计算得出的当前位移约束的支反力，m和n为正整数。

迭代收敛判断，当重新计算得到的各个支反力均满足收敛准则时，得到收敛稳定状态的有限元模型；否则重复进行当前约束调整计算，直到各个位移约束对应的支反力均满足收敛准则。

优选地，当前约束调整计算包括以下步骤：对当前组中的位移约束进行判断，当当前组中的位移约束对应的支反力均满足收敛准则时，则进行步骤标记当前组～迭代收敛判断；当存在当前组中的位移约束对应的支反力不满足收敛准则时，则进行步骤标记当前约束～迭代收敛判断。

本实施例中，经过326次迭代计算后收敛，得到吊装系统在重力作用下最终收敛稳定状态。此时目标函数为2916N，其中各支反力分别为-119N、-494N、181N、459N、476N、403N、411N、125N和248N，绝对值均小于F_s，此时，各个位移约束对应的支反力均满足收敛准则，有限元模型达到收敛稳定状态。

更进一步地，当有限元模型达到收敛稳定状态时，还可进行以下步骤中的任意一项或多项：对双吊钩吊装系统的稳定安全距离进行计算；对双吊钩吊装系统中的一个位置和吊装绳进行干涉判断；对双吊钩吊装系统的位置姿态进行计算；在有限元模型中提取吊装绳的轴向力；在有限元模型中提取吊钩上端约束的支反力；在有限元模型中提取吊装绳负载和吊钩负载。

如图4中所示，经计算得到最终稳定吊装系统在水平面上的投影。重力作用变形后，大梁组件重心G坐标为(16038，72679，9.6)，吊耳点E、F、J、K坐标为(-48，60029，-4199)、(-52，59785，2743)、(29450，57778，-4212)、(29447，57503，2578)。

经计算，该大梁组件吊装系统的计算结果如下表2所示，其中，干涉判断d₂指的是大梁组件中的撑管与吊装绳CJ的最小距离：

表2

【第四实施例】

本发明还提供了一种双吊钩吊装系统的安全性计算装置，如图5中所示，包括以下模块：

有限元建模模块501，建立由吊装对象、吊钩、吊装绳组成的吊装系统的有限元模型，在有限元模型中施加吊装系统的重力载荷；

位移约束施加模块502，在有限元模型的吊钩上添加多个弹性杆，每个弹性杆的一端与吊钩相连接，在其另一端上施加位移约束，同时在有限元模型的吊装对象上选择或者添加多个附加约束点，在多个附加约束点上分别施加位移约束，弹性杆上和附加约束点上的位移约束共同实现有限元模型的完全约束或者过度约束状态；

参数设定模块503，设定各个位移约束的参数值和收敛准则；

初始支反力计算模块504，根据有限元模型和参数值，计算各个位移约束对应的初始支反力；

初始收敛判断模块505，对各个初始支反力进行判断，当各个初始支反力均满足收敛准则时，得到收敛稳定状态的有限元模型；否则对各个位移约束进行迭代计算，直到各个位移约束对应的支反力均满足收敛准则。

进一步地，参数值包括位移约束的初始位移值初始位移增量可变位移约束个数m和最大迭代次数n，其中，j＝1，…，m，i＝1，…，n；m和n均为正整数。

优选地，收敛准则为：各个位移约束对应的支反力的绝对值均小于设定的收敛阈值F_s。

进一步地，迭代计算是利用以下迭代计算模块506进行的：当前组标记模块，依照对有限元模型的不同自由度的限制，对其中可变的各个位移约束进行分组，并根据有限元模型和参数值，计算各个位移约束对应的支反力，找出各个组中的位移约束对应的支反力的绝对值的和最大的一组，将其标记为当前组；当前位移约束标记模块，在当前组的位移约束中找出对应的支反力的绝对值最大的位移约束，将其标记为当前位移约束；当前支反力计算模块，根据割线迭代法求解当前位移约束的位移值，根据当前位移约束的位移值重新计算各个位移约束对应的支反力；迭代收敛判断模块，当重新计算得到的各个支反力均满足收敛准则时，得到收敛稳定状态的有限元模型；否则重复进行当前约束调整计算，直到各个位移约束对应的支反力均满足收敛准则。

优选地，当前约束调整计算是利用以下模块进行的：当前组判断模块，对当前组中的位移约束进行判断，当当前组中的位移约束对应的支反力均满足收敛准则时，则进行步骤标记当前组～迭代收敛判断；当前约束判断模块，当存在当前组中的位移约束对应的支反力不满足收敛准则时，则进行步骤标记当前约束～迭代收敛判断。

进一步地，割线迭代法采用以下公式：

其中，为设定的当前位移约束的初始位移值，为设定的当前位移约束的首次位移增量，m为可变位移约束个数，n为设定的最大迭代次数，为根据公式进行第i次迭代求解得到的当前位移约束的位移值，为根据进行第i次计算得出的当前位移约束的支反力，m和n为正整数。

优选地，收敛准则为：各个位移约束对应的支反力的绝对值均小于设定的收敛阈值F_s。

进一步地，当有限元模型达到收敛稳定状态之后，还可运行以下模块中的任意一个或多个：安全距离计算模块507，用于对双吊钩吊装系统的稳定安全距离进行计算；干涉判断模块508，用于对双吊钩吊装系统中的一个位置和吊装绳进行干涉判断；位置姿态计算模块509，用于对双吊钩吊装系统的位置姿态进行计算；提取模块510，用于在有限元模型中提取吊装绳负载和吊钩负载。

优选地，安全距离计算模块507包括：第一坐标提取模块，在有限元模型中提取吊装对象的重心点和吊耳点的坐标；投影计算模块，根据坐标将重心点和多个吊耳点投影到同一水平面上，多个吊耳点的投影点形成一个多边形，计算重心点的投影点到多边形各边的最小距离，即为双吊钩吊装系统的稳定安全距离。

进一步地，干涉判断模块508包括；第一位置点提取模块，根据需要指定双吊钩吊装系统中的一个位置，该一个位置为一个点或者一条线段；第二坐标提取模块，在有限元模型中提取一个点或者一条线段两端点的坐标，并提取一个吊装绳的两端点坐标，根据吊装绳的两端点坐标得到该吊装绳的两端点连线；距离计算模块，根据一个点或者一条线段的两端点的坐标和吊装绳的两端点连线，计算一个位置到两端点连线的最小距离，根据最小距离判断一个位置和吊装绳的干涉状态。

优选地，位置姿态计算模块509包括：第二位置点提取模块，根据需要指定吊装对象和吊钩上的两个位置点；第三坐标提取模块，在有限元模型中分别提取两个位置点的坐标；几何计算模块，基于两个位置点的坐标，根据空间几何学原理计算双吊钩吊装系统的位置姿态。

综上所述，利用本发明的双吊钩吊装系统安全性的计算方法，实现欠约束的双吊钩吊装系统在重力作用下的静力学计算，可计算吊装对象、吊钩和吊装绳的最终收敛稳定状态，并根据最终收敛稳定状态，计算双吊钩吊装系统的稳定安全距离、指定位置与吊载绳最小距离、吊装对象倾斜状态、吊钩位置姿态、吊装绳负载和吊钩负载，可指导吊装工艺准确地制定，从而降低双钩协同吊装的风险，具有很高的实用价值。上述实施例仅例示性说明本发明的原理及其功效，而非用于限制本发明。任何熟悉此技术的人士皆可在不违背本发明的精神及范畴下，对上述实施例进行修饰或改变。因此，举凡所属技术领域中具有通常知识者在未脱离本发明所揭示的精神与技术思想下所完成的一切等效修饰或改变，仍应由本发明的权利要求所涵盖。