一种基于高维风电预测误差模型及降维技术的发电调度方法与流程

本发明涉及电力系统的新能源发电领域，具体涉及一种基于高维风电预测误差模型及降维技术的发电调度方法。

背景技术：

随着能源消耗的日益增加，能源供给也持续紧张。以风电为代表的可再生能源得到了很大的发展。但是风电出力具有较强随机波动性、较差的功率调节能力等特点，受气象环境、风场布局等影响性较大，因此风电集群规模化接入对给电力系统的安全运行与调度规划带来巨大挑战。此外目前风电建设规划存在着“重发、轻供、不管用”，风电发展超前于相应区域电网规划，两者规划发展不协调，这些使得我国风电存在着严重的弃风现象，深究导致风电并网困难产生弃风现象的主要原因是风电出力具有随机波动性。因此为解决大规模风电并网带来的一系列问题，风电功率预测技术应运而生。虽然风电功率具有极强的波动性和随机性，但是随着时间尺度的变小，风电功率的规律性也逐渐增强，使得超短期风电功率预测成为可能。超短期风电功率预测将有助于电力系统调度部门进一步了解即将入网的风电功率，为小时级别的发电运行调度提供依据。

风电功率预测误差分布主要有正态分布、β分布、柯西分布以及拉普拉斯分布等几种传统的经验分布模型。但是β分布其求解过程非常复杂，某些预测功率区间上会出现误差概率密度无穷大的异常；柯西分布和拉普拉斯分布都是对称性分布，形状不够灵活，适用范围较固定。针对短期风电功率预测误差分布的多样性，尚未有一种分布模型，能够适应更多的误差分布特性，既能描述对称分布和单峰分布，又能描述不对称分布和多峰分布。

技术实现要素：

发明目的：本发明旨在提供一种有更高的精度，且考虑多个风电场之间相关性的影响的基于高维风电预测误差模型及降维技术的发电调度方法。

技术方案：一种基于高维风电预测误差模型及降维技术的发电调度方法，包括如下步骤：

S1：通过风电场在预设时间内的数据建立多个风电场预测误差的边缘条件概率密度函数模型；

S2：根据步骤S1得到的风电场预测误差的边缘条件概率密度函数模型，计算发电机组的日前调度计划及旋转备用容量。

进一步的，所述步骤S1通过风电场在预设时间内的数据建立多个风电场预测误差的条件概率密度函数模型，并边缘变换得到降维后的边缘条件概率密度函数模型具体为：

S1-1：获取多个风电场在预设时间内的历史出力数据及相应的点预测数据；

S1-2：利用混合偏态模型对步骤S1-1中获取的每个单一风电场的实际出力和预测出力的累积分布函数进行建模；

S1-3：利用每个风电场各自的累积分布函数将实际出力和预测值转换为0-1区间分布的数据点；

S1-4：匹配步骤S1-3中得到的所有数据点，并找到最优的Copula函数并进行参数估计；

S1-5：利用步骤S4中找到的最优Copula函数建立多个风电场预测误差的条件概率密度函数模型，并通过边缘变换得到降维后的边缘条件概率。

更进一步的，所述步骤S1-1中获取多个风电场一年内每小时的历史出力数据及相应的点预测数据具体为：将获取的多个风电场实际出力的历史数据记为p_i,t，其中，i∈[1,N]表示风电场的编号，t∈[1,T]表示历史数据的时间范围；在一年内按小时为最小单位进行记录；与实际出力相对应的点预测值记为其由各风电场的NWP数据及神经网络方法生成。

进一步的，所述步骤S1-2中利用混合偏态模型对步骤S1-1中获取的每个单一风电场的实际出力和预测出力的累积分布函数进行建模具体为：利用的混合偏态模型包括混合偏态分布，混合偏态分布由正态分布线性叠加得到；若一个随机变量X服从位置参数为μ∈R、尺度参数为σ2∈(0，∞)和偏度参数为λ∈R的偏正态分布，则它的概率密度函数是：

式中和分别为标准正态分布的密度函数和分布函数，分别表示为：

简记为X～SN(μ，σ2，λ)；当μ＝0，σ2＝1时，X为标准偏正态随机变量，记为X～SN(λ)；

混合偏态分布是多个偏态分布的线性组合；具有K个成份的基于偏态分布的混合分布模型的概率密度函数为：

式中αk为不同偏态分布在混合偏态分布中的权重系数，αk>0且α1+…+αk+…+αK＝1。

进一步的，所述步骤S1-3具体为：将各风电场实际出力p_i,t及相应的点预测值通过各自的累积分布函数转换成[0,1]区间内分布的数据点u_i,t、

其中，F_X(x)～u(0,1)，F_Y(y)～u(0,1)。

进一步的，所述步骤S1-4中找到最优的Copula函数采用基于经验Copula函数和理论Copula函数的最短欧式距离法；具体为：

设由步骤S3得到的N个风电场在[0,1]区间的数据向量U＝(u₁,u₂,…,u_N),其中u_i(i＝1,2,…,N)的概率密度函数f_i(u_i)及累积分布函数F_i(u_i)已知，其经验Copula函数可由下式求得：

式中，为示性函数，括号中的条件满足时，I＝1，反之则I＝0；{(u_1,j,u_2,j,…,u_N,j),j＝1,2,…,T}是容量为T的时间序列；为顺序统计量，1≤i₁,…,i_N≤T；

根据式(5)得到经验Copula函数后，由下式计算经验Copula函数与理论Copula函数之间的欧氏距离：

其中为相应的Copula分布函数；

Copula函数与理论Copula函数之间的欧式距离表征了Copula函数与随机变量实际分布的拟合程度；欧式距离越小，说明该Copula模型拟合程度越好，反之则越差。

更进一步的，所述步骤S1-5中建立多个风电场预测误差的条件概率密度函数模型，并通过边缘变换得到降维后的边缘条件概率密度函数模型具体为：风力发电的实际出力与它的预测值之间的联合分布以Copula函数来模拟，设x为实际出力值，y为出力预测值，则它们的联合概率密度函数f_XY可以写为：

式中f_X(x)和f_Y(y)分别为x和y的边缘概率密度函数，c为Copula函数；当给定点预测值则实际值的条件概率密度函数f_X|Y表示为：

设预测误差为e＝x-y，则预测误差的条件概率密度函数f_E|Y为：

e的取值范围为

将式(9)推广到模拟多个风电场的情况；假设是风电场1到N的点预测值，e₁,e₂,…e_N表示预测误差，e₁,e₂,…e_N的联合条件概率密度函数在给定点预测值为时，

式中表示所有风电场的点预测值的联合概率密度函数，表示它们的实际出力以及预测值的联合概率密度函数；c_N和c_2N是分别与和相对应的Copula密度函数；是每个风电场预测出力的边缘分布函数；

通过边缘变换得到高维风电场预测误差模型降维后的每个单一风电场的边缘条件概率密度函数

式中c_i,N是Copula函数。

更进一步的，所述步骤S1-6计算发电机组的日前调度计划及旋转备用容量具体为：

通过边缘变换得到高维风电场预测误差模型降维后的每个单一风电场的边缘条件概率密度函数模型，对单一风电场的边缘条件概率密度函数求均值记为旋转备用容量Z，发电机组的日前调度计划W，

W＝Z+W₀

其中W₀为除风电场外机组的发电计划容量。

本发明还提供了一种基于高维风电预测误差模型及降维技术的发电调度系统，包括：

用于通过风电场在预设时间内的数据建立多个风电场预测误差的边缘条件概率密度函数模型的单元；

用于根据风电场预测误差的边缘条件概率密度函数模型计算发电机组日前调度计划及旋转备用容量的单元。

进一步的，所述用于通过风电场在预设时间内的数据建立多个风电场预测误差的边缘条件概率密度函数模型的单元包括；

用于获取多个风电场在预设时间内的历史出力数据及相应点预测数据的单元；

用于利用混合偏态模型对获取的每个单一风电场的实际出力和预测出力的累积分布函数进行建模的单元；

用于将每个风电场各自的累积分布函数将实际出力和预测值转换为0-1区间分布的数据点的单元；

用于匹配所有数据点并找到最优的Copula函数进行参数估计的单元；

用于利用最优Copula函数建立多个风电场预测误差的条件概率密度函数模型并通过边缘变换得到降维后的边缘条件概率的单元。

有益效果：相对于现有技术，本发明采用通用分布来拟合不同风电预测区间上实际风电功率的概率密度函数PDF和累积分布函数CDF，能较好地适用任意时间尺度和幅值的风电预测误差建模，其模型拟合精度高于常规的高斯分布和β分布，且本发明不仅考虑了每个风电场预测误差与点预测值间的关系，而且考虑了多个风电场之间相关性的影响。除此之外，本发明还采用了基于混合偏态分布的预测误差分布模型，该模型是偏态分布与混合分布的结合，相对于传统误差分布模型，更加灵活可变。正态分布考虑偏态后，增加了偏态系数，可以解决风电出力条件预测误差分布中的多峰现象和重尾现象。

附图说明

图1为本发明的流程示意图；

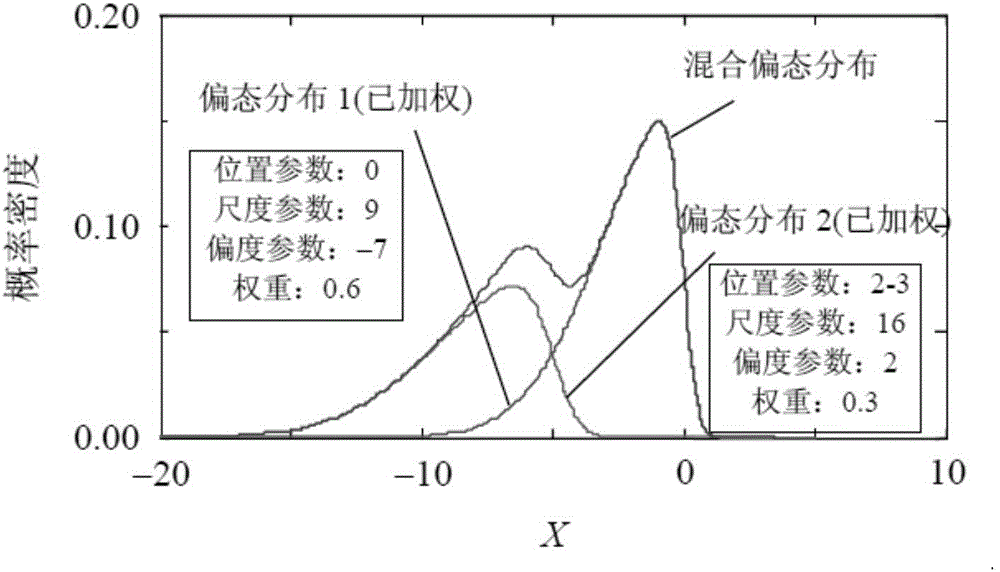
图2为本发明提供的双峰分布的混合偏态分布图；

图3为本发明提供的风电场1的实际值-预测值散点图(CDF)；

图4为本发明提供的所有风电场实际值-预测值的Gaussia copula相关系数图；

图5为本发明提供的点预测值分别为4.99MW、9.81MW时风电场1与风电场2实际出力值的联合条件分布估计图；

图6为本发明提供的点预测值分别为5.30MW、14.12MW时风电场1的条件分布估计图。

具体实施方式

下面将结合附图，对本发明的实施案例进行详细的描述；

建在同一地区的多个风电场由于地理位置相对集中，所处的气象条件和环境也大概相同，所以这些风电场间的风速具有一定的相关性，而与风速密切相关的风电的输出功率也具有一定的相关性。本发明基于考虑到多风电场出力之间的相关性，提出一种基于高维风电预测误差模型及降维技术的发电调度方法。

如图1所示，本发明所述的一种基于高维风电预测误差模型及降维技术的发电调度方法，包括如下步骤：

1)：获取多个风电场一年内每小时的历史出力数据及相应的点预测数据；具体为：将获取的江苏多个风电场实际出力的历史数据记为p_i,t，这里i∈[1,N]表示风电场的编号，t∈[1,T]表示历史数据的时间范围，在一年内按小时为最小单位进行记录，共8760个数据点。与实际出力相对应的点预测值记为其由各风电场的NWP数据(numerical weather prediection，数值天气预报)及神经网络方法生成。

2)：利用混合偏态模型对每个单一风电场的实际出力和预测出力的累积分布函数(Cumulative Distribution Function，CDF)进行建模；具体包括：混合偏态模型中的混合偏态分布是由正态分布线性叠加得到的。若一个随机变量X服从位置参数为μ∈R、尺度参数为σ2∈(0，∞)和偏度参数为λ∈R的偏正态分布，则它的概率密度函数是：

式中和分别为标准正态分布的密度函数和分布函数，分别表示为：

可简记为X～SN(μ，σ2，λ)。当μ＝0，σ2＝1时，X为标准偏正态随机变量，记为X～SN(λ)。

混合偏态模型中的混合偏态分布是多个偏态分布的线性组合。具有K个成份的基于偏态分布的混合分布模型的概率密度函数为：

式中αk为不同偏态分布在混合偏态分布中的权重系数，αk>0且α1+…+αk+…+αK＝1。

混合偏态分布可以描述非常丰富的分布情况，能够更好地描述短期风电功率误差分布的有偏性、重尾性和多峰性。双峰分布的混合偏态分布如图2所示。对概率密度函数f在(-∞,+∞)区间内积分，得到单一风电场实际出力和预测值的累积分布函数(CDF)F_X,F_Y。

3)：利用每个风电场各自的累积分布函数CDF将实际出力和预测值转换为0-1区间分布的数据点；具体为：将各风电场实际出力p_i,t及相应的点预测值通过各自的累积分布函数转换成[0,1]区间内分布的数据点u_i,t、

其中，F_X(x)～u(0,1)，F_Y(y)～u(0,1)。图3为标准化转换后的风电场1的实际值-预测值散点图。

4)：通过匹配步骤3)中得到的所有数据点，找到最优的Copula函数并进行参数估计；其中采用基于经验Copula函数(empirical Copula，EMC)和理论Copula函数(theoretical Copula Function，THC)的最短欧式距离法实现最优Copula函数(把多维随机变量的联合分布用一维边际分布连接起来的函数)的选取。测试表明，在Gumbel copula、Gaussian copula、t copula中，Gumbel copula有着最优的性能。考虑到在多变量系统中Gaussian copula比Gumbel copula更加灵活，本发明采用Gaussian copula(又称正态Copula，是多元正态分布的连接函数)进行研究。具体为：

设由步骤3)得到的N个风电场在[0,1]区间的数据向量U＝(u₁,u₂,…,u_N),其中u_i(i＝1,2,…,N)的概率密度函数f_i(u_i)及累积分布函数F_i(u_i)已知，其EMC可由下式求得：

式中，为示性函数，括号中的条件满足时，I＝1，反之则I＝0；{(u_1,j,u_2,j,…,u_N,j),j＝1,2,…,T}是容量为T的时间序列；为顺序统计量，1≤i₁,…,i_N≤T。

根据式(5)得到EMC后，可由下式计算EMC与THC之间的欧氏距离：

其中为相应的Copula分布函数。

EMC与THC之间的欧式距离表征了Copula函数与随机变量实际分布的拟合程度。欧式距离越小，说明该Copula模型拟合程度越好，反之则越差。因此选取最优的Copula函数作为描述各风电场实际出力与预测值之间的连接函数。

5)：利用步骤(4)中找到的最优Copula函数建立多个风电场预测误差的条件概率密度函数模型，并通过边缘变换得到降维后的边缘条件概率密度函数模型；

由于风速的随机性，风力发电的出力预测值与实际值之间并没有一个确定性的关系，因此它们看作一对具有相关性的随机变量，即其中一个变量的取值会对另一个变量的概率分布产生影响。风力发电的实际出力与它的预测值之间的联合分布可以Copula函数来模拟，设x为实际出力值，y为出力预测值，则它们的联合PDF(概率密度函数)f_XY可以写为：

式中f_X(x)和f_Y(y)分别为x和y的边缘PDF，c为Copula函数。当给定点预测值则实际值的CPDF(条件概率密度函数)f_X|Y可以表示为：

设预测误差为e＝x-y，则预测误差的条件概率密度函数f_E|Y为：

e的取值范围为

式(9)提供了一种利用点预测值将风力发电的条件预测误差量化的方法。它表明预测的分布包括两个方面：作为基础函数的实际出力的概率分布，以及作为可变乘子的Copula密度函数。因此，对条件预测误差的计算可以转变为对这两个函数的计算。

式(9)可以被推广到模拟多个风电场的情况。假设是风电场1到N的点预测值，e₁,e₂,…e_N表示预测误差，e₁,e₂,…e_N的联合在给定点预测值为时，如式(10)所示，

式中表示所有风电场的点预测值的联合PDF，表示它们的实际出力以及预测值的联合PDF。c_N和c_2N是分别与和相对应的Copula密度函数。是每个风电场预测出力的CDF(边缘分布函数)。

通过边缘变换可以得到高维风电场预测误差模型降维后的每个单一风电场的边缘

式中c_i,N是Copula函数，它只跟单一风电场实际出力与所有风电场出力预测值之间的相关性有关。

式(10)和式(11)不仅考虑了每个风电场预测误差与点预测值间的关系，而且考虑了所有风电场之间的相关性。式(11)中的各个预测误差的边缘CPDF之间也有联系。

本实施例中：建立多个风电场预测误差的边缘条件概率密度函数模型，并通过边缘变换得到降维后的边缘条件概率密度函数模型。图4展示了相关系数的确立结果，它清楚的显示了不同风电场的出力间、不同风电场预测值间的空间相关性，以及二者之间的联系。图5计算了当点预测值分别为4.99MW(总量的24.95％)与9.81MW(总量的49.3％)时，风电场1和2的关联条件预测误差。上图清楚地表明两个风电场条件预测误差之间的关联性。这种相关性理解为：由于相邻风电场总是处在相同的天气与环境中。而这些，预测工具是不能测出的。预测误差具有关联性。所以，当风电场发生一个较大的预测误差，相邻的其他风电场也很有可能发生误差。图6通过将估计的CPDF与风电场1的实际分布相比较判断模型的性能。左侧的直方图展示了点预测值为5.30MW下估计与实际的CPDF数据，而右侧展示了点预测值为14.12MW下的情况。这里通过低维copula函数和高维copula函数对预测值误差的条件概率密度函数模型进行了估计。

6)：根据风电场预测误差的边缘条件概率密度函数模型，计算发电机组的日前调度计划及旋转备用容量；

利用风电场预测误差的边缘条件概率密度函数模型来计算日前调度计划，它能考虑每种风电出力场景并分配相应的备用容量。为了清楚地显示之前建立的条件预测误差模型的价值，这里只考虑风电的不确定性。风电场预测误差的边缘条件概率密度函数模型包含即时和观望决策的变量及约束，风电出力的日前点预测值可以形成即时决策的约束条件。而风电实际出力的场景，通过对建立的条件预测误差模型进行采样，形成对应的观望决策约束条件。采样过程包含三个步骤：A.根据点预测值，通过式(11)建立降维后风电预测误差的条件概率密度函数模型；B.由条件概率密度函数模型生成一天内风电实际出力的大规模场景；C.通过K均值聚类技术减少场景数量以提高计算效率。具体为：

通过边缘变换得到高维风电场预测误差模型降维后的每个单一风电场的边缘条件概率密度函数模型，对单一风电场的边缘条件概率密度函数求均值记为旋转备用容量Z，发电机组的日前调度计划W，

W＝Z+W₀

其中W₀为除风电场外机组的发电计划容量。

本发明所述的一种基于高维风电预测误差模型及降维技术的发电调度系统，包括：

用于通过风电场在预设时间内的数据建立多个风电场预测误差的边缘条件概率密度函数模型的单元；

用于根据风电场预测误差的边缘条件概率密度函数模型计算发电机组日前调度计划及旋转备用容量的单元。

其中，用于通过风电场在预设时间内的数据建立多个风电场预测误差的边缘条件概率密度函数模型的单元还包括：

用于获取多个风电场在预设时间内的历史出力数据及相应点预测数据的单元；

用于利用混合偏态模型对获取的每个单一风电场的实际出力和预测出力的累积分布函数进行建模的单元；

用于将每个风电场各自的累积分布函数将实际出力和预测值转换为0-1区间分布的数据点的单元；

用于匹配所有数据点并找到最优的Copula函数进行参数估计的单元；

用于利用最优Copula函数建立多个风电场预测误差的条件概率密度函数模型并通过边缘变换得到降维后的边缘条件概率的单元。

对应上述方法实施例的描述，该发电调度系统的各组成单元能够逐步实现本发明的基于高维风电预测误差模型及降维技术的发电调度方法，达到相同的技术效果，对该系统的工作过程不再赘述。本发明先用混合偏态分布构建单个风电场的分布模型，混合偏态分布相对于正态分布考虑偏态后，增加了偏态系数，用来描述不对称分布，可以解决短期风电出力条件预测误差分布中的多峰现象和重尾现象。之后利用Copula函数对风电场实际出力与预测值及多个风电场之间进行相关性建模，建立多个风电场的高维预测误差模型并通过边缘变换进行降维，降维后的风电预测误差模型相较于常用的高斯分布、β分布有着更高的精度，不仅考虑了每个风电场预测误差与点预测值间的关系，而且可以考虑多个风电场之间相关性的影响。利用Copula理论可以将对变量联合分布的建模转变为对变量边缘分布和相依结构分别建模，极大地方便了对非独立随机变量的研究。本发明对于风电预测误差高维与低维建模和多个风电场之间的相关性的考虑具有较好的准确性和有效性。