一种冰盖下明渠输水渠道及其水力最优断面的求解方法与流程

本发明涉及一种输水渠道，具体地说是一种冰盖下明渠输水渠道及其水力最优断面的求解方法，属于灌区输水渠道规划设计技术领域。

背景技术：

水力最优断面是指面积一定的情况下使明渠输水流量最大(或流量一定的情况下使输水断面积最小)的断面。水力最优断面被广泛应用于工程实践中。公知的水力最优断面(也称为最优水力断面)是基于自由水面(无冰盖)情况下求得的水力最优断面，其最佳宽深比是(式中b为渠底宽度，h为水深,m为边坡系数)。工程中常用的梯形断面的最佳宽深比只与边坡系数m有关，而与糙率、纵坡无关。

然而，随着水资源矛盾日益突出，为避开与夏季农业灌溉用水冲突，许多渠道设计为主要在冬季冰盖下进行输水，如引黄济青工程，设计输水期为10月至翌年3月。目前冬季输水已经成为一种重要的输水方式。

公知的明渠水力最优断面是按水面不结冰设计的，没有考虑冰盖引起的湿周变化。但实际冬季冰期输水时水面有结冰，冰盖的存在增加了湿周和阻力，使过水能力减小，按非冰期(自由水面)设计的最优化断面在冰盖下输水时并不是最优断面。如果将常规的水力最优断面应用于以冬季输水为主的冰盖下输水渠道显然是不合适的，因此迫切需要设计一种具有能够增加冰盖下输水流量的水力最优断面。

技术实现要素：

针对现有技术的不足，本发明提出一种冰盖下明渠输梯形水渠道及其水力最优断面的求解方法，其能够在冰期输水时具有最大过流能力，并且能够减小水体散热，保持水温，更好的利用地热能减少结冰，从而避免冰塞、冰坝事故的发生。

本发明解决其技术问题采取的技术方案是：一种冰盖下明渠输水渠道，其特征是，包括渠底、渠道左边坡、渠道右边坡、左堤顶和右堤顶，所述渠底的左右两侧分别与渠道左边坡和渠道右边坡的下端连接，所述渠道左边坡的上端与左堤顶连接，所述渠道右边坡的上端与右堤顶连接；所述冰盖下明渠输水渠道的断面为梯形断面，在上层冰盖影响区水流的平均流速V_i和下层渠床影响区水流的平均流速V_b相同情况下进行冰盖下输水时，冰盖下明渠输水渠道水力最优断面的宽深比为：在上层冰盖影响区水流的平均流速V_i和下层渠床影响区水流的平均流速V_b不相同情况下进行冰盖下输水时：其中，b为渠底宽度，h为水深，m为边坡系数，i为渠底纵坡坡度，n_b为渠床糙率，n_i为冰盖糙率，Z₁＝n_i^3/2(∈^5/2+∈^3/2)n_b^3/2+∈⁴n_i³+n_b³，

优选地，所述冰盖下明渠输水渠道水力最优断面的宽深比是根据以下冰盖下明渠输水渠道水力最优断面的最优化模型进行求解：

目标函数是使过水断面面积最小：

A＝(b+hm)h (1)

约束条件是该过流面积下需通过指定的流量Q：

其中，Q为冰盖下明渠输水流量，b为渠底宽度，h为水深，m为边坡系数，i为渠底纵坡坡度，n_b为渠床糙率，n_i为冰盖糙率，Φ为约束函数。

优选地，所述冰盖下明渠输水渠道包括挖方渠道、填方渠道或填挖方渠道。

本发明还提供了一种冰盖下明渠输水渠道水力最优断面的求解方法，其特征是，首先建立冰盖下明渠输水渠道水力最优断面的求解模型，然后利用拉格朗日乘子法得到求解冰盖下明渠输水渠道水力最优断面的微分方程，最后根据微分方程计算出冰盖下明渠输水渠道水力最优断面的宽深比。

进一步地，所述冰盖下明渠输水渠道水力最优断面的求解方法包括以下步骤：

步骤一：建立冰盖下明渠输水渠道水力最优断面的最优化模型：

A＝(b+hm)h (1)

式中，Q为冰盖下明渠输水流量，b为渠底宽度，h为水深，m为边坡系数，i为渠底纵坡坡度，n_b为渠床糙率，n_i为冰盖糙率。

步骤二：利用拉格朗日乘子法得到求解冰盖下明渠输水渠道水力最优断面的微分方程，如式(3)所示：

步骤三：将冰盖下的水流分为上层冰盖影响区和下层渠床影响区，根据质量守恒定理有：

Q＝Q_i+Q_b

(4)

式中,Q为冰盖下明渠输水流量，Q_i为上层冰盖影响区的水流量，Q_b为下层渠床影响区的水流量；

设无量纲参数V_i为上层冰盖影响区水流的平均流速，V_b为下层渠床影响区水流的平均流速，根据谢才公式得到综合糙率的表达式，如式(5)所示：

式中，P_i为冰盖造成的湿周，P_b为渠床造成的湿周；

步骤四：设宽深比无量纲参数并对式(1)和式(2)中A和Φ求导数，并代入式(3)后将水力最优断面的最优化模型转换为一个方程，求解该方程得到冰盖下明渠输水渠道水力最优断面的宽深比。

进一步地，在步骤四中，研究表明(Chow Ven Te.(1959).Open Channel Hydraulics.McGraw-Hill,New York.)，冰盖下输水时，上层冰盖影响区水流的平均流速和下层渠床影响区水流的平均流速的平均流速都约等于整个断面水流的平均流速，即V_b＝V_i,此时∈≈1，则相应的综合糙率的表达式为：

水力最优断面的最优化模型转换的方程为:

求解式(7)所示的方程得到冰盖下明渠输水渠道水力最优断面的宽深比为：

将式(8)代入冰盖下明渠输水渠道水力最优断面最优化模型的约束条件式(2)中得到:

求解式(9)得到水深:

则渠底宽度为

式中，Q为冰盖下明渠输水流量，b为渠底宽度，h为水深，m为边坡系数，i为渠底纵坡坡度，n_b为渠床糙率，n_i为冰盖糙率。

进一步地，当冰盖下明渠输水渠道的断面为矩形断面时，即m＝0时(梯形断面就变成了矩形断面)，将m＝0代入式(8)中得到矩形断面的水力最优断面的宽深比：

此时，水深为渠底宽度为将式(11a)与式(8)相比可以看出，本发明提供的冰盖下梯形断面的水力最优断面，其最佳宽深比不仅与边坡系数m有关，也与冰盖糙率n_i、渠床糙率n_b有关(与冰盖糙率和渠床糙率之间的相对关系有关)，其底宽b是水深h的倍；而常规的水力最优断面与糙率无关(赵振兴，何建京，水力学，清华大学出版社)；

将m＝0代入式(10)中得到矩形断面的水力最优断面的水深：

式中，Q为冰盖下明渠输水流量，b为渠底宽度，h为水深，m为边坡系数，i为渠底纵坡坡度，n_b为渠床糙率，n_i为冰盖糙率。

进一步地，在步骤四中，冰盖下输水过程中上层冰盖影响区水流的平均流速与下层渠床影响区水流的平均流速不相等时，即V_b≠V_i，此时∈≠1，则水力最优断面的最优化模型转换的方程为:

求解式(12)所示的方程得到冰盖下明渠输水渠道水力最优断面的宽深比 为：

其中，

Z₁＝n_i^3/2(∈^5/2+∈^3/2)n_b^3/2+∈⁴n_i³+n_b³

式中，b为渠底宽度，h为水深，m为边坡系数，i为渠底纵坡坡度，n_b为渠床糙率，n_i为冰盖糙率。

本发明的有益效果如下：该冰盖下明渠输水渠道的冰盖下梯形断面的水力最优断面，其最优宽深比不仅与边坡系数有关，也与冰盖糙率和渠床糙率有关，而常规的水力最优断面与糙率无关；本发明冰盖下明渠输水渠道的断面可以使渠道在冰盖下输水时，过流面积一定的情况下，具有最大过流能力，或者说在过流量一定的情况下，过流面积最小。

本发明具有以下特点：

(1)以往的最优水力断面都是针对无结冰渠道，缺少冰盖下输水的水力最优断面的求解算法。而本发明建立了冰盖下输水的水力最优断面的求解模型，并利用拉格朗日乘子法，得到了求解冰盖下水力最优断面算法，并以此可以很容易得到冰盖下水力最优断面的宽深比。

(2)根据本发明提供的水力最优断面，在冰盖下输水时具有最 大的过流能力。而常规的水力最优断面在冰盖下输水时并不是“最优”断面。

(3)本发明提供的冰盖下水力最优断面算法： 当n_i＝0时(水面不结冰时n_i＝0)就变成了： 因此本发明提供的冰盖下水力最优断面的算法更加通用，常规的水力最优断面(不结冰)只是n_i＝0时的一种特例。

(4)本发明提供的冰盖下水力最优断面不仅能使明渠在冰盖下输水时具有最大过流能力，而且相比较常规水力最优断面；本发明提供的水力最优断面是一种窄深式的断面，其宽深比、水面宽度更小，这有利于地热能而保持水温，减小冬季从水面或冰面的散热量，有利于保持水温，推迟结冰时间，减小冰盖厚度，更好的利用地热能减少结冰，从而避免冰塞、冰坝事故的发明。

附图说明

图1为本发明输水渠道的水力最优断面示意图；

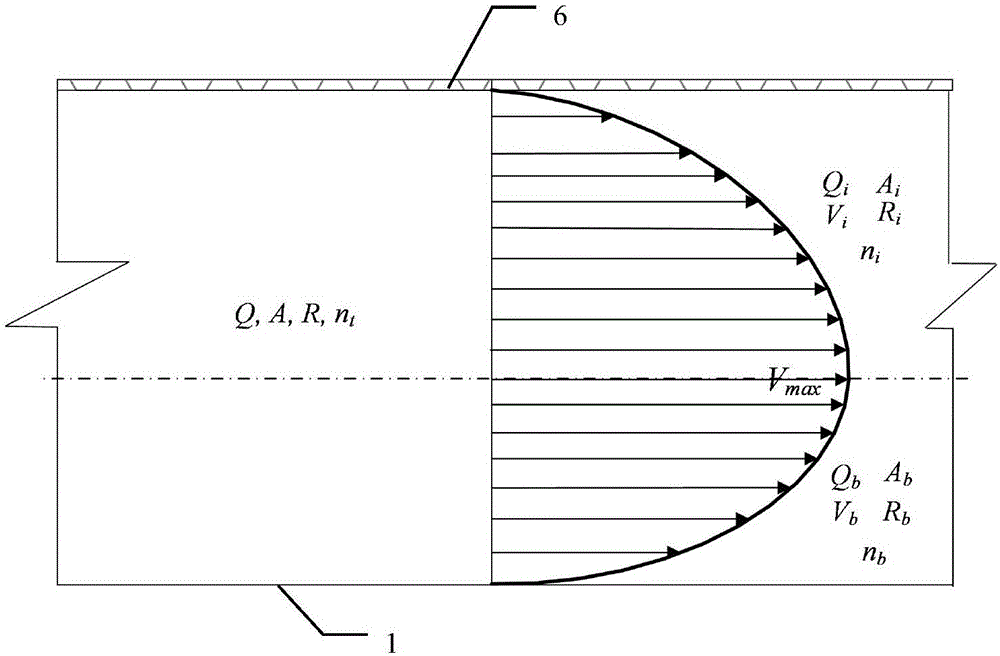
图2为冰盖下输水流速分布特性示意图；

图3为常规情况下(不结冰时)水力最优断面的形状示意图；

图4为当n_i＝n_b时冰盖下输水水力最优断面的形状示意图；

图中,

1为渠底，2为渠道左边坡，3为渠道右边坡，4为左堤顶，5为右堤顶，6为冰盖；

b为渠底宽度，h为水深，m为边坡系数，i为渠底纵坡坡度，n_b为渠床糙率，n_i为冰盖糙率，Q为冰盖下明渠输水流量，Q_i为上层冰盖影响区的水流量，Q_b为下层渠床影响区的水流量，A为冰盖下明渠 输水渠道水力断面的面积，V_i为上层冰盖影响区水流的平均流速，V_b为下层渠床影响区水流的平均流速。

具体实施方式

为能清楚说明本方案的技术特点，下面通过具体实施方式，并结合其附图，对本发明进行详细阐述。下文的公开提供了许多不同的实施例或例子用来实现本发明的不同结构。为了简化本发明的公开，下文中对特定例子的部件和设置进行描述。此外，本发明可以在不同例子中重复参考数字和/或字母。这种重复是为了简化和清楚的目的，其本身不指示所讨论各种实施例和/或设置之间的关系。应当注意，在附图中所图示的部件不一定按比例绘制。本发明省略了对公知组件和处理技术及工艺的描述以避免不必要地限制本发明。

如图1所示，本发明的一种冰盖下明渠输水渠道，它包括渠底1、渠道左边坡2、渠道右边坡3、左堤顶4和右堤顶5，所述渠底1的左右两侧分别与渠道左边坡2和渠道右边坡3的下端连接，所述渠道左边坡2的上端与左堤顶4连接，所述渠道右边坡3的上端与右堤顶5连接；所述冰盖下明渠输水渠道的断面为梯形断面，在上层冰盖影响区水流的平均流速和下层渠床影响区水流的平均流速相同情况下进行冰盖下输水时，冰盖下明渠输水渠道水力最优断面的宽深比为：水深为渠底宽度为其中，b为渠底宽度，h为水深，m为边坡系数，i为渠底纵坡坡度，n_b为渠床糙率，n_i为冰盖糙率。

所述冰盖下明渠输水渠道水力最优断面的宽深比是根据以下冰盖下明渠 输水渠道水力最优断面的最优化模型进行求解：

目标函数是使过水断面面积最小：

A＝(b+hm)h (1)

约束条件是该过流面积下需通过指定的流量Q：

其中，Q为冰盖下明渠输水流量，b为渠底宽度，h为水深，m为边坡系数，i为渠底纵坡坡度，n_b为渠床糙率，n_i为冰盖糙率，Φ为约束函数。

本发明所述的冰盖下明渠输水渠道包括挖方渠道、填方渠道或填挖方渠道。

本发明还提供了一种冰盖下明渠输水渠道水力最优断面的求解方法，首先建立冰盖下明渠输水渠道水力最优断面的求解模型，然后利用拉格朗日乘子法得到求解冰盖下明渠输水渠道水力最优断面的微分方程，最后根据微分方程计算出冰盖下明渠输水渠道水力最优断面的宽深比。

本发明所述冰盖下明渠输水渠道水力最优断面的求解方法包括以下步骤：

一、建立冰盖下明渠输水渠道水力最优断面的最优化模型：

目标函数是使过水断面面积最小：

A＝(b+hm)h (1)

约束条件是该过流面积下需通过指定的流量Q：

式中，Q为冰盖下明渠输水流量，b为渠底宽度，h为水深，m为边坡系 数，i为渠底纵坡坡度，n_b为渠床糙率，n_i为冰盖糙率，Φ为约束函数。

二、利用拉格朗日乘子法得到求解冰盖下明渠输水渠道水力最优断面的微分方程，如式(3)所示：

三、如图2所示，将冰盖下的水流分为上层冰盖影响区和下层渠床影响区，根据质量守恒定理有：

Q＝Q_i+Q_b

(4)

式中,Q为冰盖下明渠输水流量，Q_i为上层冰盖影响区的水流量，Q_b为下层渠床影响区的水流量；

设无量纲参数V_i为上层冰盖影响区水流的平均流速，V_b为下层渠床影响区水流的平均流速，根据谢才公式得到综合糙率的表达式，如式(5)所示：

式中，P_i为冰盖造成的湿周，P_b为渠床造成的湿周；

四、设宽深比无量纲参数并对式(1)和式(2)中A和Φ求导数，并代入式(3)后将水力最优断面的最优化模型转换为一个方程，求解该方程得到冰盖下明渠输水渠道水力最优断面的宽深比。

该步骤分为以下两种情况：

(1)V_b≈V_i(或∈≈1)

(1-1)研究表明(Chow Ven Te.(1959).Open Channel Hydraulics.McGraw-Hill,New York.)，冰盖下输水时，上层冰盖影响区水流的平均流速和下层渠床影响区水流的平均流速的平均流速都约等于整个断面水流的平均流速，即V_b＝V_i,此时∈≈1(∈＝V_i/V_b)，则相应的综合糙率的表达式为：

(1-2)设宽深比无量纲参数并对A、Φ求导数，代入式(3)后就可以将水力最优断面的最优化模型最终转换为以下方程:

(1-3)求解式(7)所示的方程,最终得到冰盖下使过流能力最大断面的宽深比(唯一可行解)为：

将式(8)代入冰盖下明渠输水渠道水力最优断面最优化模型的约束条件式(2)中得到:

(1-4)求解式(9)得到水深:

则渠底宽度为

式中，Q为冰盖下明渠输水流量，b为渠底宽度，h为水深，m为边坡系数，i为渠底纵坡坡度，n_b为渠床糙率，n_i为冰盖糙率。

(1-5)当冰盖下明渠输水渠道的断面为矩形断面时，即m＝0时(梯形断面就变成了矩形断面)，将m＝0代入式(8)中得到矩形断面的水力最优断面的宽深比：

此时，水深为渠底宽度为

将式(11a)与式(8)相比可以看出，本发明提供的冰盖下梯形断面的水力最优断面，其最佳宽深比不仅与边坡系数m有关，也与冰盖糙率n_i、渠床糙率n_b有关(与冰盖糙率和渠床糙率之间的相对关系有关)，其底宽b是水深h的倍；而常规的水力最优断面与糙率无关(赵振兴，何建京，水力学，清华大学出版社)；

将m＝0代入式(10)中得到矩形断面的水力最优断面的水深：

式中，Q为冰盖下明渠输水流量，b为渠底宽度，h为水深，m为边坡系数，i为渠底纵坡坡度，n_b为渠床糙率，n_i为冰盖糙率。

(2)当V_b≠V_i(或∈≠1)时

(2-1)冰盖下输水过程中上层冰盖影响区水流的平均流速与下层渠床影响区水流的平均流速不相等时，即V_b≠V_i，此时∈≠1(∈＝V_i/V_b)，则用同样的方法将水力最优断面的最优化模型转换为以下方程:

(2-1)求解式(12)所示的方程得到冰盖下明渠输水渠道水力最优断面的宽深比为：

其中，

Z₁＝n_i^3/2(∈^5/2+∈^3/2)n_b^3/2+∈⁴n_i³+n_b³

式中，b为渠底宽度，h为水深，m为边坡系数，i为渠底纵坡坡度，n_b为 渠床糙率，n_i为冰盖糙率。

本发明得到了一种冬季冰盖下输水的最优输水断面，该断面可以使明渠渠道在冰盖下输水时，过流面积一定的情况下，具有最大过流能力(或者说在过流量一定的情况下，过流面积最小)。当无冰盖时的情况下得到的最佳宽深比与常规水力最优断面的宽深比相同，本专利提供的水力最优断面计算公式应用范围更广，不仅适应与求解冰盖下的水力最优断面，也可求解无冰盖时的水力最优断面。常规的水力最优断面只是本专利提供的计算公式在n_i＝0(无冰盖)时的一种特例。冰盖下输水的水力最优断面是一种窄深式的断面，这有利于地热能而保持水温，而减轻冰害。在水力最优断面条件下，结冰时水面宽度总是小于不结冰时的水面宽度，这有利于减小水面(或冰面)散热，保持水温，减小冰害。

本发明采用的技术原理如下。

(1)冰盖下输水水力最优断面模型

如图1所示，冰盖下输水时，过水断面面积A可表示为：

A＝(b+hm)h (14)

与非冰期不同，水面宽度B、冰盖引起的湿周P_i、渠道造成的湿周P_b和总湿周P可表示为

P_i＝B＝b+2mh (15)

对梯形断面，设优化变量为h,b。根据最优断面的定义(水力最优断面是指面积一定的情况下流量最大(或流量一定的情况下输水断面积最小))，冰盖下输水的水力最优断面可表示为下述最优化问题：

最小化：A＝A(h,b) (18)

约束条件：

式中，n_t为包括冰盖和渠底的综合糙率

采用拉格朗日乘子法，上述最优化问题可以表示为：

λ为拉格朗日乘子。

联解公式(20)和(21)可以得到求解冰盖下水力最优断面的微分方程：

上式中，函数Φ中包含综合糙率n_t，综合糙率n_t与渠床糙率n_b、渠床湿周P_b、冰盖糙率n_i和冰盖湿周P_i有关。

(2)冰盖下输水水力最优断面的综合糙率

如图2所示，冰盖下的水流可以被分为上层和下层，冰盖下输水的综合糙率可用下式表示(Chow,1959)

因为R,R_i和R_b均未知，所以假设无量纲参数利用谢才公式(水力学，赵振兴，清华大学出版社)，∈可表示为

式中，V_b,V_i为渠道下层和上层水流的平均流速(见图2)

由(24)式，R_i可用∈,R_b,n_i和n_b表示：

将R_i代入(25)式,可以得到冰盖下输水的综合糙率的表达式

下面分两种情况进行讨论，一种是V_i＝V_b，即∈＝1,另一种是V_i≠V_b，即∈≠1.

(3)当V_i＝V_b或∈＝1时冰盖下输水的水力最优断面

很多学者的研究表明，冰盖下输水时，上层水流、下层水流的平均流速约等于整个断面的平均流速(Chow,1959；Gary,1987,WEI,2002；Nzhikhovskiy,1964；Uzuner,1975；Pratte,1979)。即V_b＝V_i,∈≈1,可以得到相应的综合糙率的表达式为：

将(14)、(17)、(27)式代入(19)式,函数Φ(h,b)可以表示为：

由(14)式，可以得到过流面积A(h,b)关于h和b的导数：

由(28)式,可以得到Φ(h,b)对h的导数:

式中,

用同样的方法，可以得到Φ(h,b)关于b的导数:

将式(29)、(30)、(31)代入(27)式，可以得到求解冰盖下水力最优断面的方程：

简化上式可以得到：

上式中有两个未知数，设宽深比无量纲参数η为

将η,A、P_i、P_b、P和W的表达式代入(33)式,简化后可以得到

求解上式，可以得到唯一可行解

当n_i＝0，即水面不结冰时，(36)式将变成：

上式中η_free就是公知的水面没有结冰时的水力最优断面的宽深比，也是教材中常规的明渠水力最优断面。可见(36)式是通用的表达式，教材上常规的水力最优断面只是(36)式在n_i＝0时的一种特例。

(4)冰盖下输水断面的特点(∈＝1)

①冰盖下输水的水力最优断面的宽深比总是小于常规(非结冰时)的水力最优断面。

对比η_ic((36)式)和η_free((37)式)，下式总是成立：

由(38)式可知，冰盖下输水的水力最优断面的宽深比总是小于常规(非结冰时)的水力最优断面

η_ic＜η_free (39)

这说明，冰盖下输水的水力最优断面是一种窄深式的断面，这有利于地热能而保持水温，而减轻冰害。

②冰盖下输水的水力最优断面的水面宽度总是小于常规(非结冰)水力最 优断面的水面宽度。

将η_ic(公式(36))代入式(14)、(15)和(16)可以得到直接求冰盖下的A,P_i，P_b和Q：

将(40)、(41)和(42)代入(28)，可以得到直接求冰盖下Q的公式为：

从常规水力最优断面，或从公式(41)可知，当无冰盖时(n_i＝0)，水面宽度可表示为：

式中B_free为常规水力最优断面时的水面宽度。

比较B(式(41))与B_free(式(44)),下列不等式成立：

即水力最优断面时，冰盖下的水面(冰面)宽度B_ic总是小于无冰盖时的水面宽度B_free，即：

B_ic＜B_free (46)

式(46)说明，采用冰盖下的水力最优断面，可以减小冬季从水面或冰面的散热量，有利于保持水温，推迟结冰时间，减小冰盖厚度，可以减轻冬季 冰害的危害。

③如果n_i＝n_b，由(36)式可以得到最佳宽深比和水力半径为

与教材上的常规水力最优断面的宽深比(无冰盖)相比较，当n_i＝n_b时最佳宽深比是常规最佳宽深比的一半，其形状如图3所示。可以得到水力最优断面的底、边和顶均相切与圆(半径h)

(4)水力最优断面的正常水深和临界水深计算(冰盖下)

求解(43)式，可以得到正常水深的显式表达式：

计算临界水深的通用表达式为:

式中,g为重力加速度；α为断面能量修正系数(一般α＝1.0)。

将式(40)和(41)代入式(50),式(50)可以写成：

求解式(51),显式求解冰盖下水力最优断面的临界水深的表达式为:

式中,

(5)常规水力最优断面在冰盖下输水时并不是最佳

将(49)式中的h代入(40)式中，可以得到

求解上式，可以将Q表示为A的关系为

式中，

上式表示，用冰盖下水力最优断面的宽深比得到的，一定过流面积下的过流能力。

用同样的方法，可以得到，用常规(无冰盖)水力最优断面的宽深比关系:代入式(14)、(15)和(16)，并进一步代入(28)式，可以得到常规水力最优断面在冰盖下Q₂的计算公式为：

求解上式可以得到

将与上式中的h代入式可以得到

求解上式，可以将Q₂表示为A的关系为

上式表示，用常规(无冰盖下)的水力最优断面的最佳宽深比得到的，一定过流面积下的过流能力。

但A^*＞0,m＞0,n_b＞0,n_i＞0时，用验证可以得到Q＞Q₂。

说明用常规(无冰盖下)的水力最优断面的最佳宽深比得到的水力最佳在冰盖下输水时并不是“最佳”的。

(6)冰盖下矩形断面的水力最优断面算法

当m＝0时，梯形断面就变成了矩形断面，根据公式(36)，可以得到矩形断面的水力最优断面的宽深比为：

当水面不结冰时，n_i＝0，由(61)式可以得到：β_ic＝2。与教材上的矩形断面的水力最优断面的宽深比相同。

由(43)式,可以得到矩形断面的流量计算公式:

由式(49)和式(52)，可以得到正常水深和临界水深：

(7)当V_i≠V_b或∈≠1时的水力最优断面的水力特性

当V_i≠V_b或∈≠1时，用同样的方法(式(28)至(35))，可以得到更加通用的水力最优断面求解方程：

求解上式，可以得到更加通用的最佳宽深比求解算式：

式中，

Z₁＝n_i^3/2(∈^5/2+∈^3/2)n_b^3/2+∈⁴n_i³+n_b³

当∈＝1时，由(66)式得到的η_ic值与式(36)得到的η_ic值完全相同。

以上所述只是本发明的优选实施方式，对于本技术领域的普通技术人员来说，在不脱离本发明原理的前提下，还可以做出若干改进和润饰，这些改进和润饰也被视为本发明的保护范围。