一种齿轮箱振动噪声全频域计算方法与流程

本发明涉及计算方法技术领域，具体涉及一种齿轮箱振动噪声全频域计算方法。

背景技术：
：

对于齿轮箱而言，一般激励频率在零至几千Hz内，由此产生的振动噪声分布在0～20000Hz。根据波长与结构特征尺寸的关系，或根据整体振动与局部振动在整个结构振动中的所占比例的关系，可将齿轮箱在全频域内的振动噪声分为低频、高频、中频三个频段。

对于低频段的计算，由于其结构模态稀疏，结构的动态特性主要以整体模态为主，且对边界条件敏感和对随机特性影响不敏感，适合于用确定性方法进行分析，工程上常用的是有限元和边界元等基于单元离散的分析方法。对于高频段的计算，采用有限元或边界元等确定性方法理论上是可行的，且可以获得可信的计算精度。但是由于单元数量会随着分析频率的升高而增加，会使得计算时间剧增，对于体积较大和箱壁较厚的结构，时间的增长将会达到无法接受的程度。以现有的计算硬件条件，有限元等确定性方法还只能用于低频段的振动噪声计算分析中。所以针对高频段局部模态密集，结构振动主要以局部模态为主，对边界条件相对不敏感，且对随机特性影响很敏感的特点，其计算适合于用统计性方法进行分析，工程上常用的是统计能量分析的方法。对于中频段来说，由于包含了低频段和高频段的特点，故中频段的问题处理起来要比低频段或高频段更加复杂，目前能够有效准确的计算该频段内的振动噪声的方法还在研究和发展当中。

由于不同的频段有各自的特点，故目前没有一种可以有效地进行全频域齿轮箱振动噪声分析的方法手段。

技术实现要素：
：

本发明的目的是提供一种齿轮箱振动噪声全频域计算方法，根据不同的频段各自的特点，有效地进行全频域齿轮箱振动噪声分析的方法。

本发明采用的技术方案为：一种噪声预测模型的验证试验方法，包括齿轮箱振动噪声的低频段和齿轮箱振动噪声的高频段，其特征在于：齿轮箱振动噪声的低频段采用有限元或边界元基于单元离散的分析方法求解，齿轮箱振动噪声的高频段采用统计能量分析的方法求解，综合有限元或边界元和统计能量分析方法对齿轮箱振动噪声全频域进行计算，计算方如下：

步骤一，根据计算机的运算能力确定和所能接受的计算时间长短，确定出相应的网格尺寸，再根据波长频率与网格尺寸的关系，确定出有限元或边界元的所能计算的上限频率；

步骤二，根据能量传递和存储过程中的主次关系，划定主要子系统和次要子系统，再根据主要子系统的模态数和模态重叠因子，确定出统计能量分析的下限频率；

步骤三，根据有限元或边界元所能计算的上限频率、统计能量分析的下限频率以及需要分析的最高频率三者之间的大小关系，使用有限元和统计能量分析实现齿轮箱振动噪声全频域的计算，可以得到以下6种情况：

当f_下<f_上时：

1）f_分析<f_下，则直接使用有限元或边界元进行全频域的振动噪声计算；

2）f_下<f_分析<f_上，则直接使用有限元或边界元进行全频域的振动噪声计算，或者使用有限或边界元和统计能量分析结果的均值作为重叠部分频段的振动噪声值，以得到全频域的计算结果；

3）f_上<f_分析，同情况2）；

当f_上< f_下时：

4）f_分析<f_上，则直接使用有限元或边界元进行全频域的振动噪声计算；

5）f_上<f_分析<f_下，则使用有限元或边界元的振动计算结果作为低频域的振动噪声值，高于有限元上限频率的部分使用有限元或边界元和统计能量分析结果的均值作为该频段的噪声值以得到全频域的计算结果；

6）f_下<f_分析 ，则使用有限元或边界元的振动计算结果作为低频域的振动噪声值，高于有限元上限频率并低于统计能量分析下线频率的频段部分使用两种分析方法结果的均值作为该频段的振动噪声值，使用统计能量分析计算结果作为高频段的振动噪声值，以得到全频域的计算结果。

其中，f_上为有限元或边界元所能计算的上限频率，f_下为统计能量分析的下限频率，f_分析为需要分析的最高频率。

所述的齿轮箱振动噪声中频段的计算，采用将有限元或边界元等基于单元离散的计算结果和统计能量分析的计算结果求平均值进行求解。

所述的轮箱振动噪声全频段为各频段计算结果的集合。

本发明的有益效果是：本齿轮箱振动噪声全频域计算方法，可根据不同的频段各自的特点，有效地进行全频域齿轮箱振动噪声分析的方法。

附图说明：

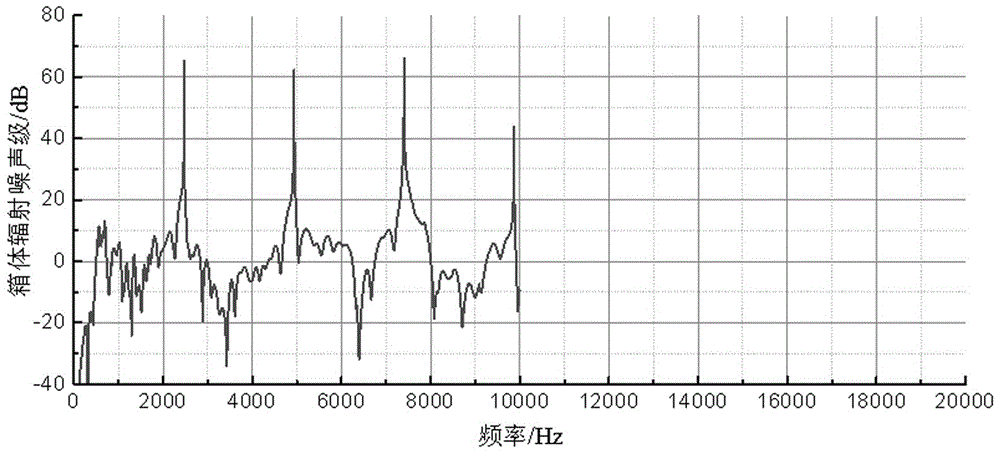
图1是本发明箱体辐射噪声的有限元或边界元的计算结果；

图2是本发明箱体辐射噪声的统计能量分析的计算结果；

图3是本发明箱体辐射噪声的全频域计算结果。

具体实施方式：

参照各图，一种齿轮箱振动噪声全频域计算方法，包括齿轮箱振动噪声的低频段和齿轮箱振动噪声的高频段，其特征在于：齿轮箱振动噪声的低频段采用有限元或边界元基于单元离散的分析方法求解，齿轮箱振动噪声的高频段采用统计能量分析的方法求解，综合有限元或边界元和统计能量分析方法对齿轮箱振动噪声全频域进行计算，计算方如下：

步骤一，根据计算机的运算能力确定和所能接受的计算时间长短，确定出相应的网格尺寸，再根据波长频率与网格尺寸的关系，确定出有限元或边界元的所能计算的上限频率；

步骤二，根据能量传递和存储过程中的主次关系，划定主要子系统和次要子系统，再根据主要子系统的模态数和模态重叠因子，确定出统计能量分析的下限频率；

步骤三，根据有限元或边界元所能计算的上限频率、统计能量分析的下限频率以及需要分析的最高频率三者之间的大小关系，使用有限元和统计能量分析实现齿轮箱振动噪声全频域的计算，可以得到以下6种情况：

当f_下<f_上时：

1）f_分析<f_下，则直接使用有限元或边界元进行全频域的振动噪声计算；

2）f_下<f_分析<f_上，则直接使用有限元或边界元进行全频域的振动噪声计算，或者使用有限或边界元和统计能量分析结果的均值作为重叠部分频段的振动噪声值，以得到全频域的计算结果；

3）f_上<f_分析，同情况2）；

当f_上< f_下时：

4）f_分析<f_上，则直接使用有限元或边界元进行全频域的振动噪声计算；

5）f_上<f_分析<f_下，则使用有限元或边界元的振动计算结果作为低频域的振动噪声值，高于有限元上限频率的部分使用有限元或边界元和统计能量分析结果的均值作为该频段的噪声值以得到全频域的计算结果；

6）f_下<f_分析 ，则使用有限元或边界元的振动计算结果作为低频域的振动噪声值，高于有限元上限频率并低于统计能量分析下线频率的频段部分使用两种分析方法结果的均值作为该频段的振动噪声值，使用统计能量分析计算结果作为高频段的振动噪声值，以得到全频域的计算结果。

其中，f_上为有限元或边界元所能计算的上限频率，f_下为统计能量分析的下限频率，f_分析为需要分析的最高频率。

所述的齿轮箱振动噪声中频段的计算，采用将有限元或边界元等基于单元离散的计算结果和统计能量分析的计算结果求平均值进行求解。所述的轮箱振动噪声全频段为各频段计算结果的集合。

因为统计能量分析的使用频率范围又受到模态数和模态重叠因子的影响，而模态数和模态重叠因子又与箱体物理尺寸息息相关，使得统计能量分析使用频率范围的下限值一般都不会太低，所以一般说来，对于齿轮箱体，有限元的上限频率值要比统计能量分析的下限频率值小，即大多数情况都属于上述的第5种和第6种情况。

对一台齿轮箱箱体进行全频域振动噪声的计算，首先采用有限元-边界元方法对该箱体的辐射噪声进行计算，结果如图1；然后采用统计能量分析方法对该箱体的辐射噪声进行计算，结果如图2。

从图1中可知有限元-边界元的上限频率是6000Hz，从图2中可知统计能量分析的下限频率是10000Hz。由于分析频段为0-20000Hz，即f_上< f_下<f_分析，可知本算例为情况6。

所以将图1中0-6000Hz频段作为齿轮箱振动低频段的计算结果，将图2中10000-20000Hz频段作为齿轮箱振动高频段的计算结果。针对高于有限元上限频率并低于统计能量分析下线频率的频段，即6000-10000Hz频段内，将两种分析方法结果的均值作为中频段的振动噪声值。则该齿轮箱全频段的箱体辐射噪声级的计算结果如图3。

由上述结果可看出，通过本发明可以得到齿轮箱在全频域内振动噪声的计算结果。