一种基于射线的三维模型切比雪夫特征提取方法与流程

本发明涉及三维模型处理领域，更具体地说，涉及一种基于射线的三维模型切比雪夫特征提取方法。

背景技术：

随着计算机硬件和软件的快速发展，以及多媒体技术、虚拟现实技术等的推广，三维模型得到越来越广泛的关注和研究。三维模型是物体的三维多边形表示，可以由计算机或者其它视屏设备进行显示。三维模型比二维模型能更真实地表示物体，因此，三维模型在生物医学、电子商务、虚拟现实、建筑设计、机械设计以及三维游戏等多个领域扮演着重要的角色。

至今，互联网上已经出现了大量的三维模型，三维模型的应用需求也在日益增大。将来，三维模型将与现在的二维图像、二维视频等一样，数量不可估计。为此，如何检索三维模型成了亟待解决的问题。近年来，大量基于内容的模型特征提取方法已被提出，其中，传统基于射线采样的三维模型特征提取算法，是选取切比雪夫球面的经纬划分交点作为终点做为采样射线，但由于要做大量的射线与面片求交运算，其特征提取速度较慢。同时，该提取方法对模型采样鲁棒性差，模型的细微的旋转变换往往导致不能精确地表达三维模型的特征。另外，当射线少时，采样率低，不能准确的反应模型特性，当射线多时，采样率高，虽然能准确表达模型特性，但其提取速度慢，同时采样信号会产生大量冗余，特征存储量大，另外在相似度计算增加计算时间，效率低。

技术实现要素：

本发明的目的在于克服现有技术中的缺点与不足，提供一种基于射线的三维模型切比雪夫特征提取方法，该特征提取方法避免了因三维模型的细微旋转和位移产生特征的巨大变化，从而增强了提取方法的鲁棒性，同时能更精细的对三维模型进行描述，能够得到高效降维的压缩感知特征。

为了达到上述目的，本发明通过下述技术方案予以实现：一种基于射线的三维模型切比雪夫特征提取方法，其特征在于：

首先，将三维网格模型进行WPCA预处理矫正，以消除三维网格模型因为方位、旋转和缩放的影响；

其次，建立模型的切比雪夫球面，对其表面进行经纬区域划分，并将WPCA预处理矫正的三维网格模型置于切比雪夫球面的单位球内，设计采样窗口；

再次，将采样窗口内的面片进行三角密集化处理，对密集点处理得到区域内的最大采样距离和最小采样距离，形成二维特征信号，即为切比雪夫特征原始信号；

最后，将切比雪夫特征原始信号进行稀疏处理，并进行二维压缩感知处理，得到低维度的压缩感知特征F_CSCR。

在上述方案中，本发明的一种基于射线的三维模型切比雪夫特征提取方法是采用基于区域窗口的统计模式，避免了因三维模型的细微旋转和位移产生特征的巨大变化，增强了提取算法的鲁棒性。其次，由于同时考虑区域的最大距离和最小距离，能够对模型的重叠部分进行细分，能更精细的对模型进行描述。最后，通过对采样的二维信号进行DCT及稀疏表达，结合二维压缩感知过程，得到高效降维的压缩感知特征。上述的WPCA为加权主成分分析法。

本发明包括以下步骤：

步骤s201：将三维网格模型进行WPCA预处理矫正；

步骤s202：建立三维网格模型的切比雪夫球面，对其表面进行经纬区域划分；设球坐标中规定仰角由Z正半轴0°到负半轴180°，球面的区域划分步长如下：

其中n_C，n_R代表球经度、纬度划分数；τ_ij表示球面上任意划分区域；

步骤s203：将最大距离特征矩阵和最小距离特征矩阵FCBV_L(n_R×n_C)和FCBV_S(n_R×n_C)都置为零矩阵；任意区域窗口τ_ij上的密集点采样点距离集合初值dis(τ_ij)＝{0}；

步骤s204：选取模型中的任意未处理面片P_k，其三角区域做密集化处理，所得交点集即该面片的点云集记为Cloud(P_k)；

步骤s205：对于任意点计算该点c_k与模型质心的距离d_k；

步骤s206：按下列公式计算点c_k所映射到球面区域窗口的序号；点c_k所对应的球坐标记为c_k＝(c_k(φ),c_k(θ),1)；

按如下公式将采样距离d_k并入相应的区域窗口τ_ij的距离集合dis(τ_ij)中：dis(τ_ij)＝dis(τ_ij)∪{d_k}；

步骤s207：如果面片P_k为最后一个面片，则进行步骤s208，否则跳转至步骤s204；

步骤s208：计算各区域窗口τ_ij上的最大距离和最小距离，生成最大距离特征矩阵和最小距离特征矩阵，如下：

步骤s209：利用DCT对二维采样信号FCBV_L(i,j),FCBV_S(i,j)进行稀疏变换形成稀疏矩阵χ_L，χ_S：

步骤s210：采用二维压缩感知，形成如下特征向量：

其中Φ₁,Φ₂为归一化的二维高斯随机测量矩阵；最后，输出F_L，F_S作为基于射线的切比雪夫压缩感知特征向量；

步骤s211：将最大特征向量和最小特征向量归并，得到压缩感知切比雪夫特征特征向量F_CRCS：

F_CRCS＝(F_L,F_S)。

所述建立模型的切比雪夫球面，对其表面进行经纬区域划分，并将WPCA预处理矫正的三维网格模型置于切比雪夫球面的单位球内，设计采样窗口是指：将切比雪夫球面的单位球体按照经线和纬线划分，在球面形成网格窗口，将WPCA预处理矫正的三维网格模型置于切比雪夫球面的单位球内，对网格窗口内的面片进行采样。

对密集点处理得到区域内的最大采样距离和最小采样距离，形成二维特征信号是指：对密集点处理得到区域内的最大采样距离和最小采样距离，按照窗口的顺序排列形成二维特征信号矩阵。

与现有技术相比，本发明具有如下优点与有益效果：本发明一种基于射线的三维模型切比雪夫特征提取方法避免了因三维模型的细微旋转和位移产生特征的巨大变化，从而增强了提取方法的鲁棒性，同时能更精细的对三维模型进行描述，能够得到高效降维的压缩感知特征。

附图说明

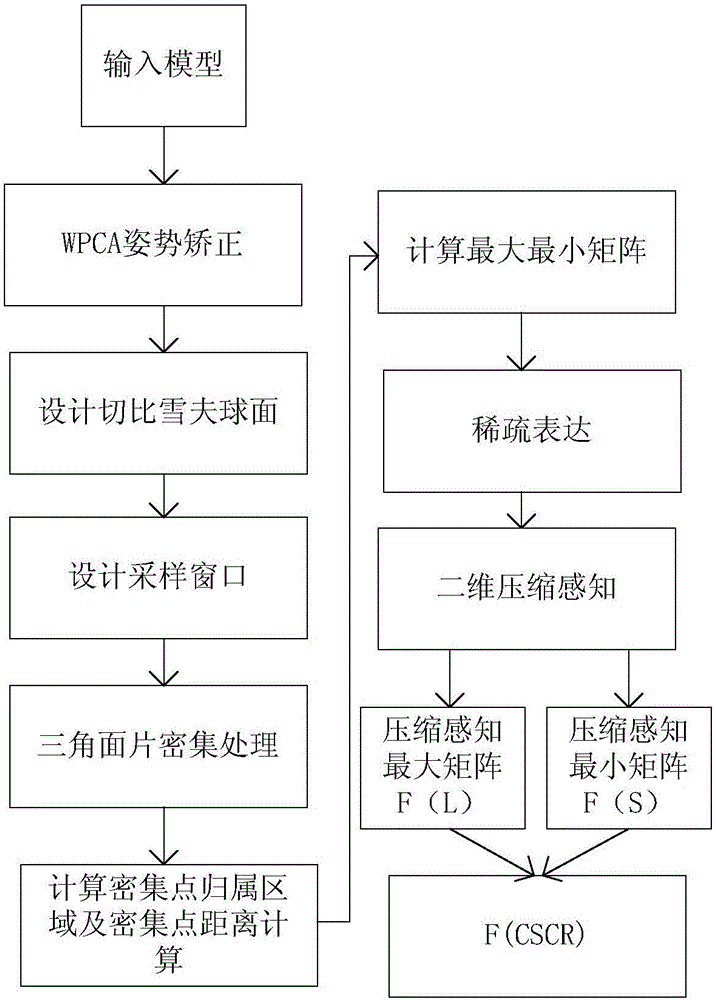
图1是本发明基于射线的三维模型切比雪夫特征提取方法的流程图；

图2是步骤s204中，模型中的任意未处理面片P_k的三角区域做密集化处理的示意图；

具体实施方式

下面结合附图与具体实施方式对本发明作进一步详细的描述。

实施例

如图1所示，本发明基于射线的三维模型切比雪夫特征提取方法是这样的：

首先，将三维网格模型进行WPCA预处理矫正，以消除三维网格模型因为方位、旋转和缩放的影响；

其次，建立模型的切比雪夫球面，对其表面进行经纬区域划分，并将WPCA预处理矫正的三维网格模型置于切比雪夫球面的单位球内，设计采样窗口；

再次，将采样窗口内的面片进行三角密集化处理，对密集点处理得到区域内的最大采样距离和最小采样距离，形成二维特征信号，即为切比雪夫特征原始信号；

最后，将切比雪夫特征原始信号进行稀疏处理，并进行二维压缩感知处理，得到低维度的压缩感知特征F_CSCR。

本发明的方法具体包括以下步骤：

步骤s201：将三维网格模型进行WPCA预处理矫正；

步骤s202：建立三维网格模型的切比雪夫球面，对其表面进行经纬区域划分；设球坐标中规定仰角由Z正半轴0°到负半轴180°，球面的区域划分步长如下：

其中n_C，n_R代表球经度、纬度划分数；τ_ij表示球面上任意划分区域；本实施例选取n_R＝32,n_C＝32。

步骤s203：将最大距离特征矩阵和最小距离特征矩阵FCBV_L(n_R×n_C)和FCBV_S(n_R×n_C)都置为零矩阵；任意区域窗口τ_ij上的密集点采样点距离集合初值dis(τ_ij)＝{0}；

步骤s204：选取模型中的任意未处理面片P_k，其三角区域按图2所示方式做密集化处理，所得交点集即该面片的点云集记为Cloud(P_k)；

步骤s205：对于任意点计算该点c_k与模型质心的距离d_k；

步骤s206：按下列公式计算点c_k所映射到球面区域窗口的序号；点c_k所对应的球坐标记为c_k＝(c_k(φ),c_k(θ),1)；

按如下公式将采样距离d_k并入相应的区域窗口τ_ij的距离集合dis(τ_ij)中：dis(τ_ij)＝dis(τ_ij)∪{d_k}；

步骤s207：如果面片P_k为最后一个面片，则进行步骤s208，否则跳转至步骤s204；

步骤s208：计算各区域窗口τ_ij上的最大距离和最小距离，生成最大距离特征矩阵和最小距离特征矩阵，如下：

步骤s209：利用DCT对二维采样信号FCBV_L(i,j),FCBV_S(i,j)进行稀疏变换形成稀疏矩阵χ_L，χ_S：

步骤s210：采用二维压缩感知，形成如下特征向量：

其中Φ₁,Φ₂为归一化的二维高斯随机测量矩阵；最后，输出F_L，F_S作为基于射线的切比雪夫压缩感知特征向量；

步骤s211：将最大特征向量和最小特征向量归并，得到压缩感知切比雪夫特征特征向量F_CRCS：

F_CRCS＝(F_L,F_S)。

上述方法中，建立模型的切比雪夫球面，对其表面进行经纬区域划分，并将WPCA预处理矫正的三维网格模型置于切比雪夫球面的单位球内，设计采样窗口是指：将切比雪夫球面的单位球体按照经线和纬线划分，在球面形成网格窗口，将WPCA预处理矫正的三维网格模型置于切比雪夫球面的单位球内，对网格窗口内的面片进行采样。

而对密集点处理得到区域内的最大采样距离和最小采样距离，形成二维特征信号是指：对密集点处理得到区域内的最大采样距离和最小采样距离，按照窗口的顺序排列形成二维特征信号矩阵。

本发明的一种基于射线的三维模型切比雪夫特征提取方法是采用基于区域窗口的统计模式，避免了因三维模型的细微旋转和位移产生特征的巨大变化，增强了提取算法的鲁棒性。其次，由于同时考虑区域的最大距离和最小距离，能够对模型的重叠部分进行细分，能更精细的对模型进行描述。最后，通过对采样的二维信号进行DCT及稀疏表达，结合二维压缩感知过程，得到高效降维的压缩感知特征。

上述实施例为本发明较佳的实施方式，但本发明的实施方式并不受上述实施例的限制，其他的任何未背离本发明的精神实质与原理下所作的改变、修饰、替代、组合、简化，均应为等效的置换方式，都包含在本发明的保护范围之内。