基于多项式极大似然估计的核电站堆芯温度场软测量方法与流程

本发明属于热工测量技术领域，特别涉及基于多项式极大似然估计的核电站堆芯温度场软测量方法。

背景技术：

随着我国经济的发展，对电力供应的需求越来越大，而非化石能源凭借着它清洁、可再生等优点，渐渐地取代化石能源的作用。核能依靠它在资源、环境和经济性方面的优势，逐步成为能源界的新宠。随着核能的发展，核安全问题受到人们越来越多的关注，对于核电站有效控制和安全控制的要求越来越高。

在压水堆核电站中，一回路的冷却剂将核燃料组件释放的热量导出反应堆，其出口温度的大小反映了燃料元件与冷却剂之间的换热情况。当堆芯温度超过限值时会发生熔融，造成核泄漏；不大的超温，尽管不会发生严重的核安全事故，但对燃料元件包壳材料产生热损伤，造成寿命损耗，多次累积仍有可能造成核泄漏严重事故。

现有的“点”温度测量，由于设置点数有限，存在监视盲区，不能全局观测堆芯温度分布。而且，温度测点即使按热通道等设计参数布置，在实际运行中，随着燃耗、氙振荡、控制棒位置等变化，热通道和热点也会发生漂移，所以并不能保证所布置的温度测点能够一直监测到堆芯内部的最高温度。目前，可应用于核电站中堆芯温度场软测量的研究尚未见记载。

研究核反应堆堆芯的温度场分布对解决核安全问题具有实际意义。而基于计算机信息处理技术进行堆芯温度场重构检测，能全景化地展示堆芯的温度分布，为核反应堆安全运行提供可视化的温度场图像，更进一步地保障了堆芯运行的安全性和经济性。

技术实现要素：

发明目的：针对现有技术中存在的问题，本发明提供基于多项式极大似然估计的核电站堆芯温度场软测量方法，该方法能够以布置在堆芯冷却剂出口的传感器采集到的温度为初始数据，在现有压水堆堆芯功率分布模型的基础上，结合稳态传热热量守恒方程，应用极大似然估计多项式拟合的方法，建立堆芯温度计算模型和堆芯导热模型，最终实现对压水堆堆芯冷却剂和堆芯燃料组件的三维温度分布的软测量。

技术方案：为解决上述技术问题，本发明提供基于多项式极大似然估计的核电站堆芯温度场软测量方法，其特征在于：包括以下步骤：

步骤一：以核电站反应堆堆芯冷却剂出口处的测点温度为离散点，采用极大似然估计多项式拟合的方法对测点温度进行数值计算处理，对其他未布置温度传感器的冷却剂出口温度进行拟合，重构得到整个堆芯冷却剂出口截面温度；

步骤二：通过反应堆结构及其回路系统中冷却剂的流动方式、热量传输特性和燃料元件的传导特性，建立堆芯温度计算模型和堆芯热传导模型，并计算得到堆芯的径向功率Q_ij、堆芯的轴向功率Q_k和每个节块的功率Q_ijk；

步骤三：根据各通道的冷却剂进/出口温度，取其平均值调用冷却剂热力参数，采用换热公式Q_ij＝c_ij·w_ij·ρ_ij·ΔT_ij，计算出冷却剂在各通道的流量w_ij；式中,ΔT_ij是各通道冷却剂进、出口温度差，Q_ij是堆芯径向功率，c_ij是各通道冷却剂的比热容，ρ_ij是各通道冷却剂的密度；如图3中，冷却剂的各通道流量即为箭头所指向的冷却剂在压水堆中流动的所有通道流量。

步骤四：利用步骤二得到的每个节块的功率Q_ijk和步骤三所得到的各个通道的冷却剂流量值w_ij，从冷却剂入口或出口的温度开始，将上一个节块的温度及对应的冷却剂密度和比热带入每个节块对应的换热公式Q_ijk＝c_ijk·w_ij·ρ_ijk·ΔT_ijk中，利用迭代、逐次逼近的方法计算下一个节块的温度值，最终得到整个堆芯的冷却剂温度分布；式中，c_ijk为每个节块冷却剂的比热容，w_i为每个冷却剂通道的流量，ρ_ijk为每个节块冷却剂的密度，ΔT_ijk为每个节块冷却剂的进出口温差。

步骤五：将步骤四所得到的核电站堆芯冷却剂的三维温度带入步骤二中的堆芯传导模型中，计算得到堆芯燃料组件各部分的三维温度分布。

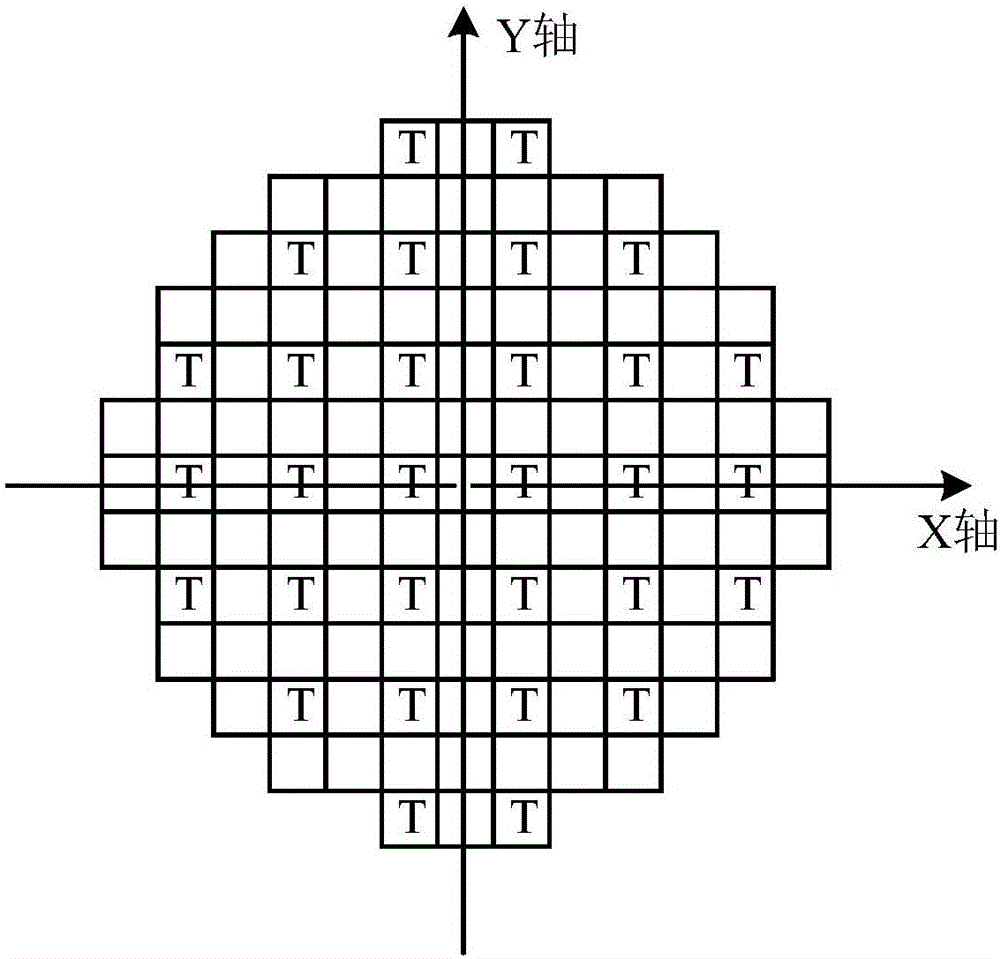
进一步的，所述步骤一中对测点温度进行计算处理的具体方法为：核电站冷却剂出口测量得到的n个温度场离散点数据为x_s,y_s,z_s，其中s＝1，2…n，x、y为传感器分布坐标，其中传感器分布坐标的原点为堆芯流量所有通道的中心通道；具体参照图2所示，堆芯里对称布置着很多燃料组件，这些组建彼此之间都有通道，所有通道的最中心极为原点，根据原点建立x轴和y轴。z为对应坐标的温度；二元k次的曲面拟合多项式拟合函数为实际散点与所得温度场多项式拟合结果的误差函数为：使误差函数达到最小值的拟合多项式函数的系数a_ij是唯一的，计算误差函数对每个系数a_ij的偏导数使其为0，即对得到的线性方程组求解即可。

进一步的，所述步骤二中的堆芯温度计算模型由以下几个部分组成：

A.堆芯通道模型：堆芯内冷却剂的横向流动较纵向流动小得多，可以不考虑通道间的质量、动量和能量交换，将堆芯内冷却剂的流动通道看作是单通道模型；

B.堆芯节块划分(参见图4)：使模型变为有限元；径向划分时，1个节块对应1个燃料组件；轴向平均划分时，尽可能使节块形状接近立方体以保证在各方向采用相同的计算方法，划分为16个节块；

C.功率分布模型：根据全堆芯各位置的中子功率预测值得到堆芯归一化的径向功率和轴向功率(这里所指的归一化均指相对径向平均功率和轴向平均功率而言)；每一节块的功率通过下式计算得到：

式中Q_ijk为每个节块的功率，Q为整个堆芯的已知功率，Q_ij为堆芯归的径向功率，Q_k为堆芯的轴向功率，g为整个堆芯的热效率。

进一步的，所述步骤二中的堆芯热传导模型(参见图5)由以下几个部分组成：

A.堆芯燃料元件传热模型：圆柱坐标系下轴向无限大一维热传导模型求解得到4πλ_rl(T₁-T₂)＝Q；

B.燃料元件与包壳之间间隙的传热模型：(T₂-T₃)h_gA₁＝Q

C.包壳管内的传热模型：圆柱坐标系下无内热源一维热传导模型求解得到

D.包壳外表面与冷却剂的对流换热模型：视为均匀壁温边界条件的大空间自然对流(T₄-T_avg)h_fA₂＝Q。

式中，T₁为燃料芯块的中心温度；T₂为燃料芯块的边缘温度；λ_r为燃料芯块的热导率；l为燃料棒的高度；T₃为包壳内表面温度；h_g为燃料芯块与包壳之间的等效传热系数；A₁为芯块外表面传热面积；T₄为包壳外表面温度；λ_c为包壳材料的热导率；r_s为包壳的外径；r_i为包壳的内径；T_avg为一回路冷却剂平均温度；h_f为包壳外表面与冷却剂之间的对流换热系数；A₂为包壳外表面传热面积。

与现有技术相比，本发明的优点在于：

(1)本发明从流动介质的温度场测量问题出发，为反应堆堆芯温度场检测提供了计算方法。利用已有的堆芯冷却剂出口温度单点测量值，通过计算模型得到堆芯内部无法安置传感器测量的截面温度，为核电站的安全运行提供了进一步的保证。

(2)本发明克服了现有点温度测量存在监视盲区和堆芯内部热点存在移动的问题，实现了对堆芯内部的全局监测。在堆芯温度场重构的基础上，计算了堆芯包壳内外表面、芯块中心及边缘的温度，为监测燃料元件是否处于“烧毁状态”提供了依据。

附图说明

图1为本发明的总体流程图；

图2为压水堆堆芯温度测点布置图；

图3为压水堆冷却剂流动路径图；

图4为堆芯的三维节块划分图；

图5为堆芯热传导示意图；

图6为极大似然估计多项式拟合方法计算流程图。

具体实施方式

下面结合附图和具体实施方式，进一步阐明本发明。

本专利实现方案的主要流程具体为(参见图1)：首先利用极大似然估计多项式拟合的方法，以堆芯冷却剂出口的温度测点作为离散数据，对压水堆堆芯冷却剂出口截面的二维温度场进行初步重构；再通过研究堆芯通道模型、堆芯节块划分和功率分布、堆芯冷却剂流量分配、堆芯热传导和传输模型，建立堆芯温度计算模型；然后调用冷却剂热力参数，利用换热公式Q＝c·w·ρ·ΔT计算得到各冷却剂通道的流量，其中ΔT是冷却剂进、出口温度差，Q是堆芯功率，c是冷却剂的比热容，ρ是冷却剂的密度；最后，从入口或出口开始，将上一个节块的温度及对应的冷却剂密度和比热带入堆芯温度计算模型，利用迭代法计算下一个节块的温度值，最终得到整个堆芯的冷却剂三维温度分布。

(1)采用的极大似然估计多项式拟合的方法对堆芯冷却剂出口二维温度场的初步重构(参见图6)：

曲面拟合所用二元k次多项式函数为首先根据堆芯冷却剂出口的有效温度测点的数量，确定函数的最高次数k。对于二元二次多项式，共有6项，6个系数a_ij，所以已知出口截面冷却剂温度散点数量要大于或等于6；对于二元三次多项式，共有10项，10个系数，所以已知出口截面冷却剂温度散点数量要大于或等于10；以此类推，二元k次多项式，共有项。

将已知温度散点数据带入误差函数中，计算误差函数对每个系数a_ij的偏导数使其为0，即可得到一组有个未知数、n个方程的线性方程组。利用MATLAB自带的rref函数，即对这组方程利用高斯消元法进行计算处理，得到的矩阵的最后一列即所求的各个系数。

(2)计算各个通道的冷却剂流量：以每个通道冷却剂的出口温度与入口温度的平均值作为设计温度，调用程序FluidLAB LiblF97计算冷却剂的比热容和密度后，采用换热公式Q＝c·w·ρ·ΔT得到每个通道相应的冷却剂流量。由于涉及调用冷却剂的比热容c、冷却剂的密度ρ等冷却剂的热力参数，采用由Prof.Hans-Joachim Kretzschmar编写的用于调取水和蒸汽物性参数的matlab程序FluidLAB LiblF97，以保证在计算过程中使用该程序进行冷却剂热力性质计算时能达到计算精度。具体调用方式为：

冷却剂比热容调用函数：cpwaterCE1＝cp_pTx_97(p,T,X)

冷却剂密度调用函数：rwaterCE1＝1/v_pTx_97(p,T,X)

式中，p为冷却剂压力，T为冷却剂温度，X为冷却剂质量。

(3)计算整个堆芯冷却剂的三维温度分布：在得到了每个通道的冷却剂流量后，从冷却剂入口温度纵向第1层节块开始正向逐层计算相应节块的出口温度，或者从重构得到的冷却剂出口温度纵向第16层的节块开始反向逐层计算相应节块的入口温度。主要的数值计算方法是迭代法，其基本思想是逐次逼近，先取一个粗糙的近似值，然后用同一个递推公式，反复校正此初值，直至达到预定精度要求为止。

本步骤中，需要先根据上一个节块的温度及对应的冷却剂密度、比热容计算下一个节块的温度的初值，再根据计算的温度初值修正本节块冷却剂的密度和比热容，从而得到进一步精确的节块温度，如此反复迭代逼近直至下个节块的温度满足精度要求。以此类推，最终得到整个堆芯的冷却剂温度分布。此时，所采用的换热公式相应地变为Q_ijk＝c_ijk·w_i·ρ_ijk·ΔT_ijk，式中Q_ijk为每个节块堆芯燃料组件的功率，前述堆芯功率分布模型计算得到，c_ijk为每个节块冷却剂的比热容，w_ij为每个冷却剂通道的流量，ρ_ijk为每个节块冷却剂的密度，ΔT_ijk为每个节块冷却剂的进出口温差。

(4)计算堆芯燃料组件各部分的温度：对堆芯传导模型求解得到：

将上步所得的每个节块冷却剂的温度带入T_avg中，就可进一步计算得到堆芯燃料组件各部分的温度。

式中，T₁为燃料芯块的中心温度；T₂为燃料芯块的边缘温度；λ_r为燃料芯块的热导率；l为燃料棒的高度；T₃为包壳内表面温度；h_g为燃料芯块与包壳之间的等效传热系数；A₁为芯块外表面传热面积；T₄为包壳外表面温度；λ_c为包壳材料的热导率；r_s为包壳的外径；r_i为包壳的内径；T_avg为一回路冷却剂平均温度；h_f为包壳外表面与冷却剂之间的对流换热系数；A₂为包壳外表面传热面积。

以上所述仅为本发明的实施例子而已，并不用于限制本发明。凡在本发明的原则之内，所作的等同替换，均应包含在本发明的保护范围之内。本发明未作详细阐述的内容属于本专业领域技术人员公知的已有技术。