基于Adaboost聚类和马尔科夫链的分布式光伏超短期预测方法与流程

本发明属于分布式光伏发电系统技术领域，尤其涉及一种基于Adaboost聚类和马尔科夫链的分布式光伏超短期预测方法。

背景技术：

近年来光伏发电装机容量不断增加，其波动性和间歇性对电力系统运行造成的冲击日渐突出。分布式光伏的超短期预测对电力系统安全经济运行有重要意义，主要体现为两个方面：第一，基于预测功率制定控制策略，降低光伏并网时功率波动对电力系统的影响，提高系统的安全性、可靠性及可控性；第二，有助于电力系统调度部门确定机组出力计划，降低系统内旋转备用，减少用电成本。在满足安全稳定的前提条件下，最大限度地消纳可再生能源逐渐成为光伏发电研究领域的重点，故功率预测对分布的以及并网的光伏发电系统的大规模发展具有实用价值。

光伏输出功率在地表光照强度的影响下表现出随机性和波动性，不同天气类型下，光伏输出功率变化规律存在明显的差异，因此在实际应用中难以使用统一的预测模型对各气象条件下的光伏出力进行预测。聚类预测是通过对输入数据进行特征提取及数据挖掘的组合预测方法，与单一预测方法相比能提高预测精度。由于高成本数值天气预报难以广泛应用于分布式光伏预测系统，当前大多数研究采用基于天气预报信息及云量信息对不同类型数据进行分类的组合预测方法，没有充分挖掘历史太阳辐射强度信息，预测精度在天气预报不准确的情况下显著下降。

技术实现要素：

本发明的目的是提供一种基于Adaboost聚类和马尔科夫链的组合预测方法，不仅在晴朗天气下能取得较好的预测效果，还提高了非晴朗天气下的预测精度。

为实现上述目的，本发明采用的技术方案是：基于Adaboost聚类和马尔科夫链的分布式光伏超短期预测方法，包括以下步骤：

步骤1、采用滑动平均法提取光照强度序列的确定性分量，统计分析得到不同天气类型的光照强度衰减因子；

步骤2、采用Adaboost改进的KNN方法对历史数据进行聚类分析，建立分类预测模型；

步骤3、采用多阶加权马尔科夫链方法预测地表太阳辐照度；

步骤4、建立光电转换模型，完成光伏功率超短期预测。

在上述的基于Adaboost聚类和马尔科夫链的分布式光伏超短期预测方法中，步骤1的实现包括：

1.1采用滑动平均法滤除光照强度的随机波动分量，提取确定性分量并选择该分量作为聚类分析的特征变量；

(1)式中y_t为原始光照强度实测值，m选择滑动平均时间窗口，Y_t为平滑处理后的滑动平均值；

1.2根据天文日地关系计算地表太阳辐照度Hottel标准晴天理论值，将历史数据与对应标准晴天理论值进行对比统计，得到不同天气类型的光照强度衰减因子经验值并输入预测模型；

(2)式中，I_mea(i)第i时刻地表光照强度，I_std(i)Hottel标准晴天理论值，m为衰减因子。

在上述的基于Adaboost聚类和马尔科夫链的分布式光伏超短期预测方法中，步骤2的实现包括：

2.1采用k-means聚类，通过设置聚类中心个数k、选择初始聚类中心，并在每次迭代中将样本归为距离最近的中心所属类别，每次迭代后重新根据类别中的样本更新聚类中心，直至前后两次中心的变化不超过设置值或者迭代次数小于设置值；

2.2采用KNN分类算法，通过此时k个最邻近样本的类别所占比例中最大的类别作为未知对象的类别；或者根据距离远近对邻近类别加权选择结果最大的类别作为未知对象的类别；

2.3采用Adaboost算法，通过训练数据学习得到某种弱分类器G_m(x)，通过对弱分类器的组合得到强分类器，即强分类器可以表示为：

(3)式中α_m为第m次计算得到的弱分类器在强分类器中的加权值。

在上述的基于Adaboost聚类和马尔科夫链的分布式光伏超短期预测方法中，步骤3的实现包括：

3.1对历史数据预处理，获得误差百分数序列，定义相对预测误差e_it为：

(4)式中为光照强度预测值，为光照强度实际值，i为每日的预测点数；N为样本数；

3.2状态划分，研究对象为Hottel标准晴天模型值与实际值之间的误差，将预处理中得到的误差百分数按实际运行经验划分为11个离散状态，其中误差小于-5％的点定义为状态1，相邻两状态的误差级差为10％，依次类推，误差大于85％的点定义为状态11；

3.3求取状态转移概率矩阵；

在m时刻太阳辐射的状态为S_i转移到m+k时刻太阳辐射的状态为S_j的转移概率为：

利用上述状态划分的结果，统计出各个步长(阶数k不同)状态变化的转移频数矩阵：

3.4计算各阶影响权重；

误差序列k阶自相关系数计算公式如下：

(7)式中x_i表示第i时段的误差，为平均误差，n为时间长度；

由(7)式求得的各阶自相关系数计算各阶影响权重：

3.5地表光照强度预测；

得到的不同步长的状态转移概率矩阵后，由预测日某时段误差百分数所在状态预测出下一采样时刻误差百分数所在某一状态的概率，并取得概率最大的一个状态为预测误差状态，从而得到对应的相对预测误差值e(t)；计算地表光照强度预测值：

I_pre(t)＝I_std(t)×(1-e(t)) (9)；

(9)式中，I_pre(t)为t时刻地表光照强度预测值，I_std(t)为t时刻标准晴天理论值，e(t)为预测计算用误差百分数。

在上述的基于Adaboost聚类和马尔科夫链的分布式光伏超短期预测方法中，步骤4的实现包括：

采用间接预测法，得到光照强度的预测数值后，通过光电转换模型计算光伏输出功率，计算公式为：

P＝ηSI[1-0.005(t₀+25)] (10)；

(10)式中，η是光电转换效率，S是用于光伏发电的有效总面积，I(t)是接收到的有效光照强度，t₀为光伏电池的工作温度。

本发明的有益效果是：本发明提出了基于Adaboost聚类和马尔科夫链的组合预测方法，该方法不仅在晴朗天气下能取得较好的预测效果，还提高了非晴朗天气下的预测精度。Adaboost改进的K近邻(KNN)算法不需要提前知道误差边界，具有自适应性，能加强弱分类器对不平衡数据集的分类效果。马尔科夫链(Markov Chain)是通过划分状态并使用状态之间的概率转移过程预测系统之后可能的发展趋势和确定未知状态，适用于对随机不确定事件进行跟踪预测。引入不同天气类型光照强度衰减因子，可以放大预测误差中的变化细节，并将幅值相对于晴空模型值较小的误差变化反映出来，显著提高了阴雨天气类型下地表光照强度的预测精度。综合多因素多步建模，具有较广的适用范围，采用工程经验建立光电转换模型简化了功率预测问题。

附图说明

图1是本发明一个实施例的超短期预测方法流程图；

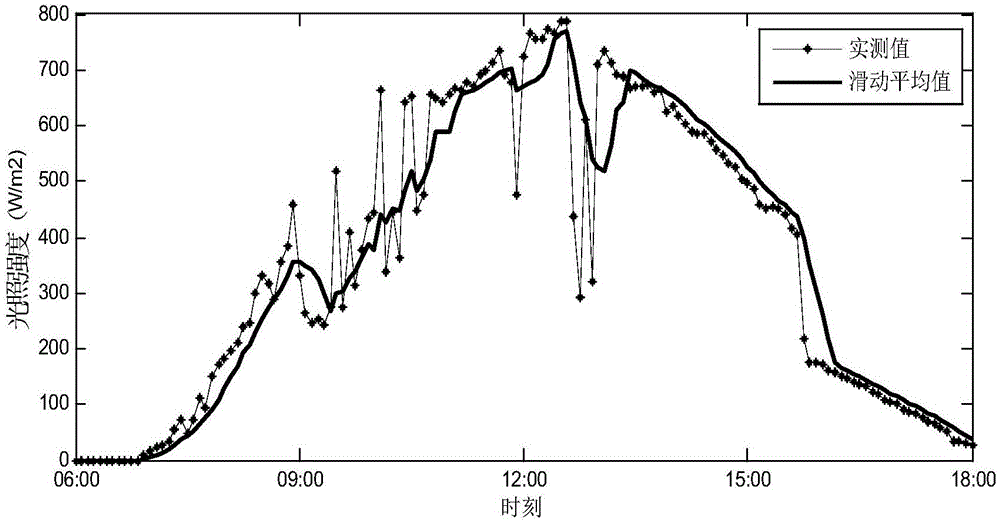
图2是本发明一个实施例滑动平均确定性变量的提取图；

图3是本发明一个实施例光照强度衰减值的区间分布图；

图4是本发明一个实施例地表光照强度的四类聚类中心图；

图5是本发明一个实施例典型日实测光照强度和标准晴天光照强度对比曲线；

图6是本发明一个实施例晴天下的模型和传统马尔科夫链的预测对比曲线；

图7是本发明一个实施例多云下的模型和传统马尔科夫链的预测对比曲线；

图8是本发明一个实施例雨天下的模型和传统马尔科夫链的预测对比曲线；

图9是本发明一个实施例阴天下的模型和传统马尔科夫链的预测对比曲线；

具体实施方式

下面结合附图对本发明的实施方式进行详细描述。

所述实施例的示例在附图中示出，其中自始至终相同或类似的标号表示相同或类似的元件或具有相同或类似功能的元件。下面通过参考附图描述的实施例是示例性的，仅用于解释本发明，而不能解释为对本发明的限制。

实施例采用如下技术方案：基于Adaboost聚类和马尔科夫链的分布式光伏超短期预测方法，包括以下步骤：

步骤1、采用滑动平均法提取光照强度序列的确定性分量，统计分析得到不同天气类型的光照强度衰减因子；

步骤2、采用Adaboost改进的KNN方法对历史数据进行聚类分析，建立分类预测模型；

步骤3、采用多阶加权马尔科夫链方法预测地表太阳辐照度；

步骤4、建立光电转换模型，完成光伏功率超短期预测。

进一步，步骤1的实现包括：

1.1采用滑动平均法滤除光照强度的随机波动分量，提取确定性分量并选择该分量作为聚类分析的特征变量；

(1)式中y_t为原始光照强度实测值，m选择滑动平均时间窗口，Y_t为平滑处理后的滑动平均值；

1.2根据天文日地关系计算地表太阳辐照度Hottel标准晴天理论值，将历史数据与对应标准晴天理论值进行对比统计，得到不同天气类型的光照强度衰减因子经验值并输入预测模型；

(2)式中，I_mea(i)第i时刻地表光照强度，I_std(i)Hottel标准晴天理论值，m为衰减因子。

进一步，步骤2的实现包括：

2.1采用k-means聚类，通过设置聚类中心个数k、选择初始聚类中心，并在每次迭代中将样本归为距离最近的中心所属类别，每次迭代后重新根据类别中的样本更新聚类中心，直至前后两次中心的变化不超过设置值或者迭代次数小于设置值；

2.2采用KNN分类算法，通过此时k个最邻近样本的类别所占比例中最大的类别作为未知对象的类别；或者根据距离远近对邻近类别加权选择结果最大的类别作为未知对象的类别；

2.3采用Adaboost算法，通过训练数据学习得到某种弱分类器G_m(x)，通过对弱分类器的组合得到强分类器，即强分类器可以表示为：

(3)式中α_m为第m次计算得到的弱分类器在强分类器中的加权值。

进一步，步骤3的实现包括：

3.1对历史数据预处理，获得误差百分数序列，定义相对预测误差e_it为：

(4)式中为光照强度预测值；为光照强度实际值；i为每日的预测点数；N为样本数；

3.2状态划分，研究对象为Hottel标准晴天模型值与实际值之间的误差，将预处理中得到的误差百分数按实际运行经验划分为11个离散状态，其中误差小于-5％的点定义为状态1，相邻两状态的误差级差为10％，依次类推，误差大于85％的点定义为状态11；

3.3求取状态转移概率矩阵；

在m时刻太阳辐射的状态为S_i转移到m+k时刻太阳辐射的状态为S_j的转移概率为：

利用上述状态划分的结果，统计出各个步长(阶数k不同)状态变化的转移频数矩阵：

3.4计算各阶影响权重；

误差序列k阶自相关系数计算公式如下：

(7)式中x_i表示第i时段的误差，为平均误差，n为时间长度；

由(7)式求得的各阶自相关系数计算各阶影响权重：

3.5地表光照强度预测；

得到的不同步长的状态转移概率矩阵后，由预测日某时段误差百分数所在状态预测出下一采样时刻误差百分数所在某一状态的概率，并取得概率最大的一个状态为预测误差状态，从而得到对应的相对预测误差值e(t)；计算地表光照强度预测值：

I_pre(t)＝I_std(t)×(1-e(t)) (9)；

(9)式中，I_pre(t)为t时刻地表光照强度预测值，I_std(t)为t时刻标准晴天理论值，e(t)为预测计算用误差百分数。

更进一步，步骤4的实现包括：

采用间接预测法，得到光照强度的预测数值后，通过光电转换模型计算光伏输出功率，计算公式为：

P＝ηSI[1-0.005(t₀+25)] (10)；

(10)式中，η是光电转换效率，S是用于光伏发电的有效总面积，I(t)是接收到的有效光照强度，t₀为光伏电池的工作温度。

实施例1

为了提高非晴天情况下的预测精度，提出一种基于Adaboost聚类和马尔科夫链的分布式光伏超短期预测方法，采用滑动平均法提取光照强度序列的确定性分量，统计分析得到不同天气类型的光照强度衰减因子；采用Adaboost改进的KNN方法对历史数据的聚类分析，建立分类模型；结合基于误差序列的多阶加权马尔科夫链实现未来时刻地表光照强度的预测，最后通过光电转换模型实现分布式光伏发电超短期预测。

实施例1通过以下技术方案得以解决：

一种基于Adaboost聚类和马尔科夫链的分布式光伏超短期预测方法，包括以下步骤：

S1，采用滑动平均法提取光照强度序列的确定性分量，统计分析得到不同天气类型的光照强度衰减因子；

S2，采用Adaboost改进的KNN方法对历史数据的聚类分析，建立分类模型；

S3，采用多阶加权马尔科夫链方法预测地表太阳辐照度；

S4，建立光电转换模型，完成光伏功率超短期预测。

所述步骤S1中采用滑动平均法提取光照强度序列的确定性分量，统计分析得到不同天气类型的光照强度衰减因子的流程如下：

选择滑动平均法滤除光照强度的随机波动分量，提取确定性分量并选择该分量作为聚类分析的特征变量。设原始光照强度实测值为y_t，选择滑动平均时间窗口m，平滑处理后的滑动平均值为Y_t。

地表光照强度在云层遮挡时刻有不同程度的下降，第i时刻地表光照强度I_mea(i)与Hottel标准晴天理论值I_std(i)之间存在不同的倍率关系，记为衰减因子m。其表达式如下所示：

不同天气类型下，地表辐照度较地外辐照度的衰减程度不一样。

所述步骤S2采用Adaboost改进的KNN方法对历史数据的聚类分析的预测流程为：

1)批量输入训练数据，提取数据的数学特征，根据KNN确定弱分类器G_m(x)

的个数；

2)确定Adaboost学习过程中的迭代次数k，初始化各样本数据的权重d_mi。

3)根据权重选择样本点，得到新的训练子集，用具有权值分布的训练数据训练弱分类器G_m(x)，用G_m(x)对所有样本进行分类，计算该弱分类器G_m(x)在训练集下的误差率e_m及其在最终分类器中的系数α_m。

4)提高被正确分类的样本权重，降低被错误分类的样本权重，为下一轮迭代更新数据样本的权重分布：

得到下一轮权重后返回步骤(3)进行下一轮迭代，直到迭代次数达到设置值或误差率达到某个设定的足够小的值。

所述步骤S3采用多阶加权马尔科夫链方法预测地表太阳辐照度流程如下：

I、对历史数据预处理，获得误差百分数序列，定义相对预测误差e_it为：

其中为光照强度预测值；及为光照强度实际值；i为每日的预测点数；N为样本数。

II、将预处理中得到的误差百分数按实际运行经验划分为11个离散状态，其中误差小于-5％的点定义为状态1，相邻两状态的误差级差为10％，依次类推，误差大于85％的点定义为状态11。

III、利用上述状态划分的结果，统计出各个步长(阶数k不同)状态变化的转移频数矩阵：

在m时刻太阳辐射的状态为S_i转移到m+k时刻太阳辐射的状态为S_j的的转移概率为：

IV、误差序列k阶自相关系数计算公式如下：

其中x_i表示第i时段的误差，为平均误差，n为时间长度。由求得的各阶自相关系数计算各阶影响权重：

V、得到的不同步长的状态转移概率矩阵后，由预测日某时段误差百分数所在状态预测出下一采样时刻误差百分数所在某一状态的概率，并取得概率最大的一个状态为预测误差状态，从而得到对应的预测误差值，由下式完成当前时刻的预测：

I_pre(t)＝I_std(t)×(1-e(t)) (23)

其中，I_pre(t)为t时刻地表光照强度预测值，I_std(t)为t时刻标准晴天理论值，e(t)为预测计算用误差百分数。

所述S4建立光电转换模型流程如下：

采用间接预测法，得到光照强度的预测数值后，通过光电转换模型计算光伏输出功率，计算公式如下所示：

P＝ηSI[1-0.005(t₀+25)] (24)

其中，η是光电转换效率(％)，S是用于光伏发电的有效总面积(m²)，

I(t)是接收到的有效光照强度(kW/m²)，t₀为光伏电池的工作温度(℃)。

实施例2

一种基于Adaboost聚类和马尔科夫链的分布式光伏超短期预测方法，如图1所示，包括以下步骤：

①采用滑动平均法提取光照强度序列的确定性分量，统计分析得到不同天气类型的光照强度衰减因子。

在实施例2中，为提取光照强度序列的确定性分量，反映光照强度平均变化趋势，选择30min的时间窗口进行平滑处理，以实际数据为例，其处理效果如图2所示。统计2015年～2016年历史记录数据与对应标准晴天模型数据，得到四种典型天气类型下(晴天、多云、雨天、阴天)衰减值的频率分布如图3所示，分布区间分别为[0,0.3)、[0.3,0.6)、[0.6,0.8)、[0.8,1]。各典型天气类型下的衰减系数计算结果如表1所示。

表1典型天气类型的衰减系数

②采用Adaboost改进的KNN方法对历史数据的聚类分析，建立分类模型。

在实施例2中，结合武汉某光伏实验平台气象监测设备2015年10月-2016年3月(实际有效数据量为130天)实时采样间隔为5min的光照强度数据及温度数据，将提取的光照强度序列确定性分量作为聚类程序的特征输入量，得到聚类中心如图4所示；由KNN和Adaboost程序完成分类，迭代次数为7次，结合网络气象记录得到的历史天气信息检验历史数据分类的准确性，结果如下表所示：

表2天气分类结果

③采用多阶加权马尔科夫链方法预测地表太阳辐照度。

(一)、对历史数据预处理，获得误差百分数序列；

研究对象为标准晴天模型与实际值之间的差值，典型日光照强度曲线图如图5所示，图中显示差值状态主要包括平稳区、波动区和骤变区，计算得到研究时段内平稳区差值总体分布在10％之内，波动区差值达到30％～40％，骤变区差值由于云的遮挡有时甚至超过70％。

(二)、状态划分，计算状态转移概率矩阵；

将预处理中得到的误差百分数按实际运行经验划分为11个离散状态，其中误差小于-5％的点定义为状态1，相邻两状态的误差级差为10％，依次类推，误差大于85％的点定义为状态11，区间划分如下表所示：

表3随机状态区间

统计出各个步长(阶数k不同)状态变化的转移频数矩阵，可计算各阶11×11的转移概率矩阵：

(三)、预测地表光照强度；

在步骤1和步骤2的基础上，历史数据被划分为晴天、多云、雨天和阴天四大类分别进行预测，本实施例选择对预测日9:00至15:00时段的光照强度进行间隔5min的滚动预测，这里选取平均绝对百分比误差对预测效果进行评价：

其中，x为实测值；为预测值；P为光伏装机容量。

历史数据按照图2方法被划分为晴天、多云、雨天和阴天作为相似日训练样本集，统计确定晴天光照强度衰减因子为0.83，输入晴天预测子模型，预测结果如图6所示；多云光照强度衰减因子为0.69，输入多云预测子模型，预测结果如图7所示；雨天光照强度衰减因子为0.35，输入雨天预测子模型，预测结果如图8所示；阴天光照强度衰减因子为0.12，输入阴天预测子模型，预测结果如图9所示。其平均绝对百分比预测误差对比如下表所示：

表4不同模型预测误差MAPE比较值

实施例2中采用某光伏实验平台某典型日前3个月的数据为基础时间序列，对典型日6小时的地表光照强度进行预测。预测结果显示本发明所提聚类组合预测模型预测效果整体优于传统马尔科夫链预测模型。对于大幅度高频率震荡的多云类天气及光照强度大幅下降的阴雨天气，传统马尔科夫链模型预测误差有所降低，很难有规律的跟踪光照强度幅值的快速变化，且阴天变化的细节不能得到很好的分析，引入衰减系数m后预测模型对光照强度的跌落反应更准确，减少了峰值、谷值的错误预报，提高了在晴天情况和非晴天情况下的预测精度。

④建立光电转换模型，完成光伏功率超短期预测。

实施例2中实验平台采用英利YL175P-23b型多晶硅电池板，转换效率为15％，得到光照强度的预测数值后，通过光电转换模型计算光伏输出功率，计算公式如下所示：

P＝ηSI[1-0.005(t₀+25)] (27)

其中，η是光电转换效率(％)，S是用于光伏发电的有效总面积(m²)，I(t)是接收到的有效光照强度(kW/m²)，t₀为光伏电池的工作温度(℃)。

应当理解的是，本说明书未详细阐述的部分均属于现有技术。

虽然以上结合附图描述了本发明的具体实施方式，但是本领域普通技术人员应当理解，这些仅是举例说明，可以对这些实施方式做出多种变形或修改，而不背离本发明的原理和实质。本发明的范围仅由所附权利要求书限定。