二维三角网格生成方法及系统与流程

本发明涉及计算机图形处理技术领域，尤其涉及一种二维三角网格生成方法及系统。

背景技术：

在计算机图形学领域中，二维三角网格是几何离散表示中最广泛的形式，大多数对象最终都要转化为二维三角网格，从而能够进行高效的渲染和偏微分方程的数值求解。可以说，生成二维三角网格是几何处理应用中最重要的步骤之一。但是，许多数值应用(如有限体积法、离散外微分、时空网格法等)都需要高质量的二维三角网格，如果能够使用全锐角的二维三角网格，将会大大减轻计算难度。

为了实现稳定的数值模拟，研究者们提出了许多方法来避免二维三角网格中出现过小和过大的角。目前，高质量的二维三角网格生成方法可以分为构造法和迭代法。通常，构造法仅提供输入的边界，然后通过在内部或者边界插入Steiner点来产生所需的三角网格；相反，迭代法开始于一个已有的二维三角网格，然后通过迭代地插入、删除或移动Steiner点来提高该二维三角网格的质量(例如，使用最优Delaunay三角化的方法，即ODT方法，其通过一些平滑步骤可以产生较好形状的三角剖分，并且可以适用于各向异性的情况。

另外，还有一些方法结合了构造法与迭代法，通过修改连接关系和顶点的位置来保证二维三角网格中的角的上限与下限。例如，使用平面直线图作为约束，使角度范围缩小到30°和100°之间(后文也称作CVT方法)；保证角度在30°和120°之间的一致Delaunay三角化方法(后文也称作CDT方法)；再例如，基于Voronoi图中的短边会对网格质量产生较大影响，利用能量函数最小化三角形外心和内心的距离的方法(后文也称作OVD方法)。然而，这些方法尽管能够在一定程度上约束大角和小角，但是所生成的二维三角网格仍会包含钝角。

为了生成高质量无钝角的二维三角网格，目前，研究者们还提出了启发式方法、调整最大泊松圆盘的空间密度的方法、分治的方法以及避免直角的方法、最小化代价函数方法(后文也称作Vanderzee方法)等。

然而，这些方法或者不能避免过小的角度，或者不能保证产生全锐角的三角网格。

技术实现要素：

为解决上述现有技术中存在的问题，根据本发明的一个实施例，提供一种二维三角网格生成方法，包括：

步骤1)、根据给定的边界形状，生成初始的二维三角网格；其中，可使用CVT方法生成初始的二维三角网格；

步骤2)、在二维三角网格中寻找所有的簇；其中，每个簇为包括一个钝角三角形和与该钝角三角形邻近的两个或更多三角形的整体，并且簇与簇之间不重合；

步骤3)、在每个簇内插入Steiner点，以生成新的二维三角网格。

上述方法中，每个簇包括一个钝角三角形和与该钝角三角形邻近的两个三角形。

上述方法中，在步骤2)中，采用如下步骤得到包括n个三角形的簇，其中n大于等于3：

步骤a)、寻找一个钝角三角形，作为簇的部分并且作为参照三角形；

步骤b)、寻找参照三角形的最长边邻接的三角形，

如果找到的三角形是无限的或者是属于另一个簇的非钝角三角形，则寻找参照三角形的非最长边邻接的三角形，如果找到的三角形不是无限的且不是属于另一个簇的非钝角三角形，则将该三角形作为簇的部分并且作为参照三角形，否则结束，

如果找到的三角形是钝角三角形，则将该钝角三角形与步骤a)中找到的钝角三角形并入一个簇，

否则，将参照三角形的最长边邻接的三角形作为簇的部分并且作为参照三角形，

重复本步骤直到找到n个三角形。

上述方法中，步骤3)中，在每个簇内插入Steiner点之前，还包括：

分别以所述簇的每条边为直径作圆，得到每个圆在所述簇的内部的交点；

从中选择没有被其他圆覆盖的交点，由所选择的交点形成封闭的多边形；

在所述封闭的多边形内获得没有被圆覆盖的点；

将该点的位置作为Steiner点要插入的位置。

上述方法中，还包括：

步骤4)、对所述新的二维三角网格进行平滑和优化处理。其中，可使用CVT方法对所述新的二维三角网格进行平滑处理；使用OVD方法对平滑后的二维三角网格进行优化处理。

步骤4)还包括：

在对所述新的二维三角网格进行平滑和优化处理之后，若有钝角产生，则返回步骤2)。

根据本发明的一个实施例，还提供一种二维三角网格生成系统，包括：

初始化装置，用于根据给定的边界形状，生成初始的二维三角网格；

簇选择装置，用于在二维三角网格中寻找所有的簇；其中，每个簇为包括一个钝角三角形和与该钝角三角形邻近的两个或更多三角形的整体，并且簇与簇之间不重合；

更新装置，用于在每个簇内插入Steiner点，以生成新的二维三角网格。

上述系统中，还包括：

处理装置，用于对所述新的二维三角网格进行平滑和优化处理。

通过实验证明，本发明提供的二维三角网格生成方法和系统可以保证生成全锐角的二维三角网格，并且可以优化较小的角度，从而能够保持良好的二维三角网格形状结构。

附图说明

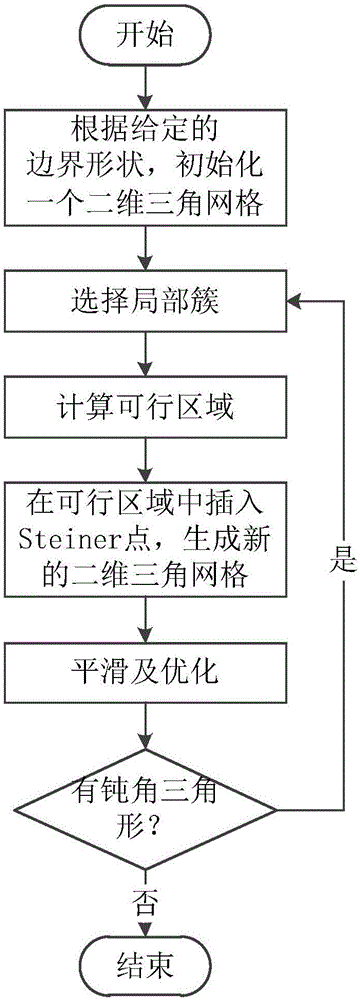
图1是根据本发明一个实施例的二维三角网格生成方法的流程图；

图2(a)-2(d)根据一个示例给出了根据本发明一个实施例的二维三角网格生成方法的示意图；

图3根据本发明的一个示例给出了簇和插入Steiner点后的二维三角网格的示意图；

图4(a)-4(e)示出在输入手形边界时，五种二维三角网格生成方法的对比示意图(均匀密度)；

图5(a)-5(e)示出在输入猫形边界时，五种二维三角网格生成方法的对比示意图(均匀密度)；

图6(a)-6(e)示出在输入海豚边界时，五种二维三角网格生成方法的对比示意图(均匀密度)；

图7(a)-7(e)示出在输入星形边界时，五种二维三角网格生成方法的对比示意图(自适应密度)；

图8(a)-8(e)示出在输入大象边界时，五种二维三角网格生成方法的对比示意图(自适应密度)；

图9(a)-9(e)示出在输入蝙蝠边界时，五种二维三角网格生成方法的对比示意图(自适应密度)；

图10示出五种二维三角网格生成方法在不同输入边界上的网格质量统计参数；

图11(a)-11(c)示出四种现有的二维三角网格生成方法与本发明提供的二维三角网络生成方法的平均统计分析示意图；

图12是本发明与现有Vanderzee方法的对比示意图。

具体实施方式

下面结合附图以及具体实施例对本发明解决的技术问题、采用的技术方案以及实现的技术效果进行清楚、完整的描述。显然，所描述的实施例仅是本申请的一部分实施例，并不是全部实施例。基于本申请中的实施例，本领域普通技术人员在不付出创造性劳动的前提下，所获得的所有其它等同或明显变型的实施例均落在本发明的保护范围内。本发明实施例可以按照权利要求中限定和涵盖的多种不同方式来具体化。

根据本发明的一个实施例，提供一种二维三角网格生成方法。

概括而言，该方法包括：

根据给定的边界形状，生成初始的二维三角网格；在二维三角网格中寻找所有的簇；其中，每个簇为包括一个钝角三角形和与该钝角三角形邻近的两个或更多三角形的整体，并且簇与簇之间不重合；在每个簇内插入Steiner点，以生成新的二维三角网格。

以下结合附图1对该二维三角网格生成方法实施例的步骤展开具体描述：

第一步：根据给定的边界形状，初始化二维三角网格。

在输入边界形状后，根据该边界形状，初始化一个二维三角网格。

举例而言，可采用上文提到的CVT方法来实现该二维三角网格的初始化，而且本领域技术人员应理解，也可以使用其他现有的二维三角网格生成方法来生成初始二维三角网格。以青蛙形边界为例，生成的初始二维三角网格如图2(a)所示。

第二步：在二维三角网格中寻找所有的簇。

簇是二维三角网格中的局部部分，簇可以包括一个钝角三角形和在该钝角三角形附近的两个或更多三角形，其中，这些三角形构成一个整体形状(即不会相互隔开)。参见图3所示的例子，其中，一个簇包含三个三角形(以灰色表示)，右下方的三角形为当前二维三角网格中的钝角三角形，也就是本发明需要去除的三角形，而另外两个灰色三角形为其附近的三角形，图3中A、B、C、D、E分别表示多边形的顶点，R、N、O、P、Q分别表示多边形各条边的中点。

优选地，由三个三角形构成一个簇，即构成五边形的簇，这样做的理由在于：对于四边形的簇(即由两个三角形构成一个簇)来说，其中不可能会找到一个可行区域(该可行区域将在后文中进行描述)，而且会形成度数为4的顶点，这种顶点不适于做三角网格中的顶点；对于六边形(七、八边形等也是类似的)的簇(即由四个三角形构成一个簇)，由于四个三角形有很大的自由度，所以很容易形成不规则的六边形，这样，插入Steiner点之后，会形成许多钝角，从而减缓本方法的收敛速度。而使用五边形可以更快的收敛，不至于产生过多的新的钝角三角形。

下面以五边形簇为例描述簇的构成过程(应理解，其他形状的簇可以类似地构造)：

首先，找到二维三角网格中的一个钝角三角形；

接着，将与该钝角三角形的最长边邻接的三角形作为第一邻接三角形；

随后，选择与第一邻接三角形的最长边邻接的三角形作为第二邻接三角形；该钝角三角形、第一邻接三角形和第二邻接三角形构成一个簇。

然而，需要注意的是，上述构成过程中存在如下特殊的情况：当最长边邻接的三角形是无限的或者已经在别的簇中并且不是钝角三角形(即非钝角三角形)时，则选择另外的边所邻接的三角形，如果找到符合条件的三角形(即不是无限的，并且不是属于别簇的非钝角三角形)则将其并入簇中，否则结束。另外，如果找到的邻接三角形为钝角三角形(即另一个簇中的钝角三角形)，则将这两个钝角三角形合并到一个五边形簇中。

所以，在二维三角网格中找到所有符合条件的簇时，该簇的数目小于或等于钝角三角形的个数。

第三步：计算每个簇中的可行区域。

仍以五边形簇为例，可行区域的计算方法如下：

首先，分别以五边形簇的五条边为直径作圆(如图2(b)、图3所示)；

其次，在五边形簇的内部找到五个圆形成的交点(如图3所示)；

接着，在这些交点中选择没有被其他圆覆盖的交点，将这些交点形成一个封闭的多边形；该封闭的多边形内的区域为可行区域。

对于二维三角网格中的每个簇，按上述方法计算其可行区域。

这里，选择可行区域的理由在于：钝角三角形通常满足一个条件，即最大边上的中线小于该边长的一半，若插入新的Steiner点，则会产生五条线段；此时，为避免五条线段间的夹角不会形成钝角，则插入的Steiner点不能被圆覆盖，这样，边上的中线会大于该边长的一半，从而形成锐角。

第四步：在每个簇的可行区域中插入Steiner点，从而二维三角网格局部连接将产生变化。

在定义了每个簇的可行区域之后，在可行区域中随机计算一个点的位置。如果这个点的位置被圆覆盖，则放弃该点的位置，重新产生新的点，直到产生的点的位置没有被圆覆盖，则该点的位置为有效位置，如图2(c)和图3所示。之后，将新的Steiner点插入到所有簇的有效位置，如图2(d)所示。在插入Steiner点之后，钝角三角形大部分被消除，但是，可能会产生不规则的网格结构，这在图2(d)中用圆圈标出，这种不规则的二维三角网格结构将在下一步通过平滑和优化处理消除。

第五步：执行平滑和优化处理以提高二维三角网格的质量，若有钝角产生则返回第二步。

对于一个正五边形簇来说，插入Steiner点不会产生不规则的情况。但是，由于五边形簇的不规则性，插入Steiner点之后或许会形成小于30°的小角。为了解决插入Steiner点之后网格不规则的问题，可以首先对二维三角网格进行平滑，如使用CVT方法进行平滑处理；之后对平滑后的二维三角网格进行优化，如使用OVD方法进行优化处理。

本领域技术人员应理解，也可以采用其他现有方法对网格进行平滑和优化处理。

然而，这种平滑和优化处理可能又会产生新的钝角三角形，因此返回第二步重复Steiner点插入、平滑、优化过程，直到产生一个没有钝角三角形和尖锐角的网格。

下文通过实验来评估本发明提供的二维三角网格生成方法的性能。其中，实验平台为具有英特尔i7 3.60GH的中央处理器，16GBRAM和64位windows 7操作系统的计算机，在该平台上使用CGAL计算几何算法库设计了二维三角网格生成系统。

在实验中，为评估二维三角网格质量的好坏，采用D.-M.Yan等人提出的方法，使用Q_min和Q_avg评估三角网格的质量。其中，Q_min代表最小三角形质量，Q_avg代表平均三角形质量；并且，使用θ_min代表二维三角网格中的最小角，代表二维三角网格中所有三角形中最小角的平均值，θ_max代表二维三角网格中的最大角。另外，本发明也统计了小于30°或者大于90°的角的百分比，在与当前最先进方法作对比时，引入了非锐角的比例p(小于30°和大于90°角的百分比的总和)，钝角三角形的数量n和标准偏差σ。本发明对均匀密度三角网格和自适应变密度三角网格的质量都做了详尽的分析，并将本发明提供的方法与现有先进的方法(如CDT，CVT，OVD和ODT等)进行了对比。

均匀密度网格的优化的例子如图4(a)-4(e)、图5(a)-5(e)以及图6(a)-6(e)所示，自适应密度网格如图7(a)-7(e)、图8(a)-8(e)以及图9(a)-9(e)所示。(图4(a)、5(a)、6(a)、7(a)、8(a)和9(a))，(图4(b)、5(b)、6(b)、7(b)、8(b)和9(b))，(图4(c)、5(c)、6(c)、7(c)、8(c)和9(c))，(图4(d)、5(d)、6(d)、7(d)、8(d)和9(d))，(图4(e)、5(e)、6(e)、7(e)、8(e)和9(e))分别对应CDT、CVT、OVD、ODT和本发明提供的方法。例子的统计数据如图10所示，对于每个例子，将CDT，CVT，OVD和ODT四种方法与本发明提出的方法进行对比。此外为了对比分析，利用多次实验的平均值作为平均参数以减少随机性。

统计对比如图11(a)-11(c)所示，其中图11(a)显示最小角，最大角和平均角的统计量，可以看出，本发明提出的方法具有更大的θ_min和更小的θ_max，虽然ODT方法也有较好的表现，但是本发明提供的方法仍具有一个显著的提升。

三角网格质量的评价(Q_avg和Q_min)如图11(b)所示。根据本发明的结果显示，在均匀和自适应密度的情况下，本发明提供的方法能产生一个显著的提高。对于各个方法在非锐角角度百分比的表现，通过图11(c)可以发现，本发明提供的方法的百分比几乎为0。

此外，本方法以圆盘作为输入边界与全锐角方法Vanderzee方法进行了对比。如图12所示，显示了两种方法的角度统计直方图、非锐角的比例p(小于30°和大于90°角百分比的总和)，钝角三角形的数量n和标准偏差σ。可以看出，虽然两种方法都达到了锐角化(p＝0，n＝0)，但是，本发明提供的方法所有角的统计角度更接近60°，并具有更小的标准偏差σ，更大最小角度θ_min。因此，本发明提供的方法会生成更均匀的三角网格，产生更好的网格结构。

根据本发明的一个实施例，还提供一种二维三角网格生成系统，包括：初始化装置，用于根据给定的边界形状，生成初始的二维三角网格；簇选择装置，用于在二维三角网格中寻找所有的簇；其中，每个簇为包括一个钝角三角形和与该钝角三角形邻近的两个或更多三角形的整体，并且簇与簇之间不重合；更新装置，用于在每个簇内插入Steiner点，以生成新的二维三角网格；处理装置，用于对新的二维三角网格进行平滑和优化处理。

至此，已经结合附图所示的优选实施方式描述了本发明的技术方案，但是，本领域技术人员容易理解的是，本发明的保护范围显然不局限于这些具体实施方式。在不偏离本发明的原理的前提下，本领域技术人员可以对相关技术特征作出等同的更改或替换，这些更改或替换之后的技术方案都将落入本发明的保护范围之内。