一种轨迹相似度计算方法与流程
本发明属于计算机应用领域,特别涉及一种轨迹相似度计算方法。
背景技术:
随着传感器技术和个人智能设备的发展,GPS设备被广泛用于追踪移动物体(人、车、动物等),每天都有大量的轨迹数据在不断产生。轨迹是移动物体随着时间变化而在空间中留下的时空数据序列,随着物联网、城市计算等领域的推动,时空数据的存储与分析已经成为数据库和机器学习领域的一个研究热点,通过分析这些轨迹数据能为各行各业带来巨大的推动力,例如:通过分析游乐场游客的运动轨迹规划游乐场基础设施建设、分析优秀足球运动员的移动模式、分析台风的频繁移动路径等。
计算轨迹间相似性度量是轨迹分析重要研究内容之一。基于轨迹相似性度量算法,可以对轨迹进行的聚类、分类、检索等。许多学者在轨迹相似性度量算法上进行了大量的研究,提出了很多高性能算法,应用比较广泛的相似性度量有DTW(动态时间归整)。DTW算法基于动态规划的思想找出轨迹点之间的最佳匹配,可以有效解决局部时间偏移问题和轨迹不等长问题,其最早的应用领域为语音识别,后被引入到时间序列分析。最长公共子序列距离算法——LCSS算法,可以有效消除轨迹数据中噪声的干扰,但由于采用得分机制没有考虑到匹配点之间的间隔点,相似性度量精度不高。EDR也采用得分机制,考虑到了匹配点之间的间隔点,较LCSS更加精确;ERP在EDR的基础上采用参考点的方式作为未匹配点的惩罚值,但参考点的选取对结果影响很大。对DTW、LCSS、ERP、EDR、SPaDe等算法,在大量时间序列数据集进行了多组比较实验,实验结果表明DTW在多数数据集上都取得最高的查询准确度。但是DTW对采样频率较敏感,且没有将轨迹形状作为计算轨迹相似度要素,导致其计算精度不够完美。
本发明公开了一种基于段的动态时间归整算法(Segment–based Dynamic Time Warping,SDTW),SDTW算法可以减少对采样频率的敏感性;采用点间时间距离的计算方式,将时间维度的差异与空间纬度的差异统一考虑,并可通过参数调节,改变各维度权重;使用段间距离代替点间距离,将轨迹形状纳入计算要素,并通过参数调整,修正形状因子,提高轨迹相似性度量算法的精度。
技术实现要素:
发明目的:针对现有技术中存在的问题,本发明提供一种轨迹相似度计算方法,可以降低轨迹采样频率对算法精确性的影响,提高轨迹相似性度量算法的精确性。
技术方案:为解决上述技术问题,本发明提供一种轨迹相似度计算方法,包括如下步骤:
步骤一:通过用户手持GPS设备采集用户时空数据,并取两条轨迹R和S;
步骤二:将经纬度坐标转换为通用横轴墨卡托投影坐标系,并使用卡尔曼滤波算法对轨迹数据进行滤波处理;
步骤三:结合点段距离和点间欧氏距离,计算两条轨迹R和S中每点间改进空间距离;
步骤四:计算两条轨迹R和S中每点间预测距离;
步骤五:使用步骤三和步骤四的结果和段间角距离,计算两条轨迹R和S中每段间距离;
步骤六:计算两条轨迹R和S的累积距离;
步骤七:将步骤六的结果进行归一化处理。
进一步的,步骤三中计算两条轨迹R和S中每点间改进距离的具体计算方法如下:取轨迹R中的第i个轨迹点Pi(xi,yi),轨迹S中的第j个轨迹点SPj(xj,yj),定义distps(Pi,SPj)为Pi和SPj的点段距离,定义distps(SPj,Pi)为SPj和Pi的点段距离,distps(Pi,SPj)≠distps(SPj,Pi);计算distps(Pi,SPj)的方法如下:
步骤3.1:点段距离即点到另外一点的替代轨迹段的距离,故首先求SPj的替代轨迹段,替代SPj参与距离计算,点的替代轨迹段的定义如下:
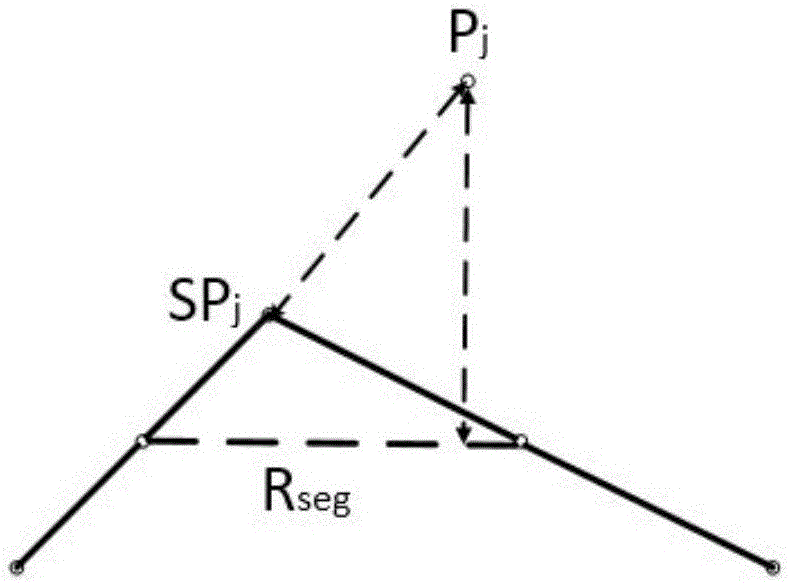
SPj的空间坐标为(xj,yj),取该取样点前后两个点SPj-1和SPj+1的空间坐标为(xj-1,yj-1)和(xj+1,yj+1);取点(xj,yj)与(xj-1,yj-1)的中点为Pmid1(xmid1,ymid1),取点(xj,yj)与点(xj+1,yj+1)的中点为Pmid2(xmid2,ymid2);点Pmid1与点Pmid2形成的线段Rseg即为(xj,yj)的替代轨迹段;如果(xj,yj)为起点则(xj-1,yj-1)等于(xj,yj),如果(xj,yj)为终点则(xj+1,yj+1)等于(xj,yj);
其中(xmid1,ymid1)、(xmid1,ymid1)的计算公式为:
步骤3.2:计算点Pi到Rseg之间的最短距离distps(Pi,Rseg),其计算方法如下:
其中r=(xmid2-xmid1)×(xi-xmid1)+(ymid2-ymid1)×(yi-ymid1);Lseg即为派生段的长度;dx=(xmid1+(xmid2-xmid1)×(r/Lseg));dy=(ymid1+(ymid2-ymid1)×(r/Lseg));distps(SPj,Pi)的计算方式与distps(Pi,Rseg)相同;
步骤3.3:求Pi到待SPj的欧几里得距离disteuc(Pi,SPj),其计算公式为:
步骤3.4:Pi与SPj的改进空间距离distp(Pi,SPj)的计算公式为:
distp(Pi,SPj)=(min{disteuc(Pi,SPj),distps(Pi,SPj)}+min{disteuc(Pi,SPj),distmin(SPj,Pi)})/2。
步骤四中计算轨迹R中的第i个轨迹点Pi(xi,yi,ti)和轨迹S中的第j个轨迹点SPj(xj,yj,tj)的预测距离时,两点间的预测距离的具体计算步骤如下:
步骤4.1:比较点Pi与点SPj的时间先后关系,设时间大的点为A,时间小的点为B;其时间差Δt=tA-tB;
步骤4.2:求点B的预测位置B',假设B点为一个运动点,遍历各个点的时间,寻找tB+Δt时B点处于哪两个轨迹点之间,即其预测位置在哪里,假定在tB+Δt时B点处于第i-1个和第i个点之间,则对于B点的预测位置B'的空间坐标(xB′,yB′)计算公式如下:
假定轨迹上任意两点之间的运动为匀速直线运动,故可求出两点之间运动速度,其求解公式如下:
如果时间tB+Δt在B轨迹上不存在,则B′计算如下:
其中N为B点所在轨迹的点的总数目;
步骤4.3:计算A和B的预测距离,计算公式如下:
distt(A,B)=dist(A,B′)
其中dist(A,B′)为A和B′的在空间坐标上的欧几里得距离。
步骤五中计算两条轨迹R和S中每段间距离的具体步骤如下:
步骤5.1:其中Si为轨迹R的第i段,SSj为轨迹S的第j段;求Si和SSj的角度θ,Si的两个端点为Pi(xi,yi)和Pi+1(xi+1,yi+1),SSj的两个端点为SPj(xj,yj)和SPj+1(xj+1,yj+1),其角度θ的计算公式为:
θ=|arctan2(yi+1-yi,xi+1-xi)-arctan2(yj+1-yj,xj+1-xj)|
步骤5.2:段间的时空距离为段的两端点的时空距离之和,因此Si与SSj的段间距离dists(Si,SSj)的计算公式为:
dists(Si,SSj)=f(θ)(distst(Pi,SPj)+distst(Pi+1,SPj+1))
步骤5.3:求f(θ),其计算公式为:
其中:ω为可调节参数形状负因子,ω越大距离对形状因素越不敏感,其中ω=1,distsmid(Si,SSj)为中点Si和SSj中点的时空距离,distmax(R,S)为轨迹R和轨迹S的任意两点间最大时空距离。引入的原因为:只有当段间时空距离较近时,形状因素才更有意义,因此使用动态调整形状因素的权重。
步骤六中进行归一化处理,即将累积距离归一化到[0,1]之间,其中,0表示两条轨迹完全无关,1表示两条轨迹完全相似的具体步骤如下:
其中,D表示缩放因子,用来描述相似度对累积距离的敏感度,累积距离相同的情况下,当D较大时相似度较高,当D较小时相似度较低。
本发明结合点段距离与点间欧式距离,给出了改进点间距离的解决方案。为了将轨迹数据在时间维度与空间维度进行统一度量,使得结果具有可解释性。本算法改进点间时间距离计算方法,提出了预测距离,预测距离就是时间小点的预测位置点到时间大点的欧式距离,这样将时间度量转化为空间度量。使用段间距离代替点间距离,将轨迹形状纳入计算要素,并通过参数调整,修正形状因子,提高轨迹相似性度量算法的精度。段间距离由点间距离和形状负因子的乘积计算而来,其中点间距离为改进点间空间距离与预测距离的加权求和,形状负因子由段间夹角变形计算而来。基于步骤三的段间距离矩阵,使用类似于DTW的递归计算的方法,计算两条轨迹的累积距离。然后对输出结果统一进行累积距离,进行归一化处理。
与现有技术相比,本发明的优点在于:
降低轨迹采样方式对算法精确性的影响;将轨迹形状纳入轨迹相似性度量算法的考虑范围,并且可以通过调节参数,修正形状因素对计算结果的影响;将时间维度与空间纬度的度量统一,加强时间与空间的联系,并可通过调节参数改变各维度的权重,提高轨迹相似性度量算法的精确性。
附图说明
图1为本发明的总体流程图;
图2为本发明公开的点间空间距离的计算方法示意图;
图3为本发明公开的预测距离执行过程示意图;
图4为本发明开的段间距离的计算示意图。
具体实施方式
下面结合附图和具体实施方式,进一步阐明本发明。
如图1所述,本发明的实施步骤如下:
步骤1:通过用户手持GPS设备(手机、PAD等)采集用户时空数据。并取其中两条轨迹R和S。
步骤2:将经纬度坐标转换为通用横轴墨卡托投影坐标,并使用卡尔曼滤波算法对轨迹数据进行滤波处理。
步骤3:结合点段距离和点间欧氏距离,计算R和S中每点间改进空间距离。
步骤4:计算R和S中每点间预测距离
步骤5:使用步骤3和步骤4的结果和段间角距离,计算R和S中每段间距离。
步骤6:计算R和S的累积距离。
步骤7:将步骤6的结果进行归一化处理
在本例中,本发明首先需要收集用户的时空数据,然后取出其中两条进行计算。由于采集到的空间数据使用经纬度坐标,所以要将其转化为二维的通用横轴墨卡托投影坐标。由于采集设备存在一定误差,因此需要使用卡尔曼滤波算法对轨迹进行滤波处理。
求R与S的每个点的空间距离,图1是计算改进点间空间距离的示意图,以R中的第i个轨迹点Pi(xi,yi)和S中的第j个轨迹点SPj(xj,yj)的空间距离计算过程为例。定义distps(Pi,SPj)为Pi和SPj的点段距离,定义distps(SPj,Pi)为SPj和Pi的点段距离,distps(Pi,SPj)≠distps(SPj,Pi),下面以distps(Pi,SPj)的计算为例。
首先求点SPj的替代轨迹段Rseg的两个端点Pmid1(xmid1,ymid1)、Pmid2(xmid2,ymid2),其计算公式为:
然后计算点Pi到Rseg之间的最短距离,由点到段的最短距离计算公式[10]可知distps(Pi,Rseg)的计算公式如下:
其中r=(xmid2-xmid1)×(xi-xmid1)+(ymid2-ymid1)×(yi-ymid1);Lseg即为派生段的长度;dx=(xmid1+(xmid2-xmid1)×(r/Lseg));dy=(ymid1+(ymid2-ymid1)×(r/Lseg))。distps(SPj,Pi)的计算方式与distps(Pi,Rseg)相同。
此外,还存在两点本身就很接近的情况,因此还需要求Pi到待SPj的欧几里得距离disteuc(Pi,SPj),其计算公式为:
则Pi与SPj的改进空间距离distp(Pi,SPj)的计算公式为:
distp(Pi,SPj)=(min{disteuc(Pi,SPj),distps(Pi,SPj)}+min{disteuc(Pi,SPj),distmin(SPj,Pi)})/2
求R与S的每个点的时间维度的距离--预测距离,图2展示了预测距离执行示意图,其中,实心点表示取样点,空心点表示预测距离根据对应点的时间进行补正后预测用来计算距离的点。各个点之上的数字表示到达该点的时间。虚线表示对应点之间的预测距离。
在计算R中的第i个轨迹点Pi(xi,yi,ti)和S中的第j个轨迹点SPj(xj,yj,tj)的预测距离时,首先比较点Pi与点SPj的时间先后关系,设时间大的点为A,时间小的点为B。其时间差Δt=tA-tB。
然后求点B的预测位置B′,假设B点为一个运动点,遍历各个点的时间,寻找tB+Δt时B点处于哪两个轨迹点之间,即其预测位置在哪里。假定在tB+Δt时B点处于第i-1个和第i个点之间,则对于B点的预测位置B′的空间坐标(xB′,yB′)计算公式如下:
假定轨迹上任意两点之间的运动为匀速直线运动,故可求出两点之间运动速度,其求解公式如下:
如果时间tB+Δt在B轨迹上不存在,则B′计算如下:
其中N为B点所在轨迹的点的总数目。
最后,最后A和B的预测距离计算公式如下:
distt(A,B)=dist(A,B′)
其中dist(A,B′)为A和B′的在空间坐标上的欧几里得距离。
求R与S的每个轨迹段之间的距离,图3展示了段间距离的计算示意图,点间距离既包括空间距离也包括时间距离,因此需要结合步步骤3和步骤4的计算结果,点Pi与SPj的时空距离distst(Pi,SPj)的计算公式为:
distst(Pi,SPj)=distp(Pi,SPj)+t×distt(Pi,SPj)
其中t为时间敏感度,t越大距离对时间维度越敏感,当t=0时忽略时间维度。
将轨迹段间夹角引入计算。假定Si为轨迹R的第i段,SSj为轨迹S的第j段。以这两段的距离计算为例。
首先求Si和SSj的角度θ,Si的两个端点为Pi(xi,yi)和Pi+1(xi+1,yi+1),SSj的两个端点为SPj(xj,yj)和SPj+1(xj+1,yj+1),其角度θ的计算公式为:
θ=|arctan2(yi+1-yi,xi+1-xi)-arctan2(yj+1-yj,xj+1-xj)|
段间的时空距离为段的两端点的时空距离之和,因此Si与SSj的段间距离dists(Si,SSj)的计算公式为:
dists(Si,SSj)=f(θ)(distst(Pi,SPj)+distst(Pi+1,SPj+1))
其中f(θ)的计算公式为:
其中:ω为可调节参数形状负因子,ω越大距离对形状因素越不敏感,若无特殊需求取ω=1即可。distsmid(Si,SSj)为中点Si和SSj中点的时空距离,distmax(R,S)为轨迹R和轨迹S的任意两点间最大时空距离。引入的原因为:只有当段间时空距离较近时,形状因素才更有意义,因此使用动态调整形状因素的权重。
使用步骤4的结果求两条轨迹的累积距离,累积距离的计算过程如下:
其中n为轨迹R的线段数,m为轨迹S的线段数,Head(R)表示轨迹R第一个段S1;Rest(R)表示轨迹R除S1后形成的新轨迹。
步骤4的输出结果为累积距离,其与相似性呈反向关系,而且两条不同轨迹的累积距离会有很大的差异,不能带来直观的对比。所以需要将累积距离进行归一化处理,即将累积距离归一化到[0,1]之间,其中,0表示两条轨迹完全无关,1表示两条轨迹完全相似。归一化函数采用反正切型函数,其计算公式如下式所示:
其中,D表示缩放因子,用来描述相似度对累积距离的敏感度,累积距离相同的情况下,当D较大时相似度较高,当D较小时相似度较低。
以上所述仅为本发明的实施例子而已,并不用于限制本发明。凡在本发明的原则之内,所作的等同替换,均应包含在本发明的保护范围之内。本发明未作详细阐述的内容属于本专业领域技术人员公知的已有技术。
- 还没有人留言评论。精彩留言会获得点赞!