初始样本选择方法及装置与流程

本发明涉及聚类技术领域，更具体地说，涉及一种初始样本选择方法及装置。

背景技术：

在数据挖掘过程中，通常会应用到聚类。聚类是将物理或抽象对象的集合(即样本集合)分成由类似的对象组成的多个类的过程。由聚类所生成的簇是一组数据对象的集合，这些对象与同一个簇中的对象彼此相似，与其他簇中的对象相异。目前，在较常用的聚类算法中，有一类聚类算法，例如，K-Means算法，K-Medoids算法等，在算法开始之前，需要从样本集合中选择k个样本作为初始样本(也叫初始聚类中心)，这个过程一般是在样本集合中随机选择k个样本作为初始样本。然而，不同的初始样本所导致的算法的收敛速度也不同，还会影响最终的聚类效果。因此，随机选择k个初始样本容易出现聚类算法的收敛速度慢、聚类效果差的问题。

因此，如何选择初始样本以克服聚类算法的收敛速度慢、聚类效果差的问题成为亟待解决的问题。

技术实现要素：

本发明的目的是提供一种初始样本选择方法及装置，以克服聚类算法的收敛速度慢、聚类效果差的问题。

为实现上述目的，本发明提供了如下技术方案：

一种初始样本选择方法，包括：

构建样本集合中样本的原始连通图；所述原始连通图中的每一个节点表征所述样本集合中的一个样本，所述原始连通图中的节点两两相连，所述原始连通图中任意两个节点之间边的权重为该两个节点所表征的两个样本的相似度；

生成所述原始连通图的最小生成树；

删除所述最小生成树中相似度最小的K-1条边，得到K个子连通图，K为聚类算法需要选择的初始样本的个数；

从每一个所述子连通图中的节点对应的样本中选择一个样本作为初始样本。

本发明实施例用通过上述方法获取的K个子连通图模拟样本的分布情况，因而从K个子连通图中选择的初始样本更接近真实的聚类中心，基于本发明提供的初始样本选择方法选择的初始样本，克服了通过随机选择初始样本点导致聚类算法的收敛速度慢、聚类效果差的问题。

上述方法，优选的，所述从每一个所述子连通图中的节点对应的样本中选择一个样本作为初始样本，包括：

从每一个所述子连通图中的节点对应的样本中，随机选择一个样本作为初始样本。

上述方法，优选的，所述从每一个所述子连通图中的节点对应的样本中选择一个样本作为初始样本，包括：

对于所述子连通图中的节点对应的样本中的每一个样本，将该样本到所述子连通图中的节点对应的样本中的其它样本之间的相似度求和，得到与该样本对应的求和结果；

选择与最大求和结果对应的样本作为初始样本。

与前一实施例相比，本实施例所选择的初始样本更加接近真实的聚类中心。

上述方法，优选的，所述生成所述原始连通图的最小生成树，包括：

从所述样本集合中选择一个样本作为所述最小生成树的初始节点；

将所述样本集合中未加入所述最小生成树的样本依次加入所述最小生成树，包括：每次将一个样本加入所述最小生成树之后，获取每一个未加入所述最小生成树的样本，与已加入所述最小生成树中的各个样本之间的相似度；确定最大相似度；将该最大相似度对应的一个未加入所述最小生成树的样本与该最大相似度对应的已加入所述最小生成树的样本相连，直至所有样本均加入到所述最小生成树。

上述方法，优选的，所述生成所述原始连通图的最小生成树，包括：

按照两两样本之间的相似度从大到小的顺序，依次将满足预设条件的两个样本相连，直至所述样本集合中的每一个样本均与所述样本集合中的至少一个其它样本相连；

其中，两个样本满足预设条件包括：所述两个样本相连后，所有已连接的样本未构成任何回路。

一种初始样本选择装置，包括：

构建模块，用于构建样本集合中样本的原始连通图；所述原始连通图中的每一个节点表征所述样本集合中的一个样本，所述原始连通图中的节点两两相连，所述原始连通图中任意两个节点之间边的权重为该两个节点所表征的两个样本的相似度；

生成模块，用于生成所述原始连通图的最小生成树；

删除模块，用于删除所述最小生成树中相似度最小的K-1条边，得到K个子连通图，K为聚类算法需要选择的初始样本的个数；

选择模块，用于从每一个所述子连通图中的节点对应的样本中选择一个样本作为初始样本。

本发明实施例用通过上述装置获取的K个子连通图模拟样本的分布情况，因而从K个子连通图中选择的初始样本更接近真实的聚类中心，基于本发明提供的初始样本选择装置选择的初始样本，克服了通过随机选择初始样本点导致聚类算法的收敛速度慢、聚类效果差的问题。

上述装置，优选的，所述选择模块包括：

第一选择单元，用于从每一个所述子连通图中的节点对应的样本中，随机选择一个样本作为初始样本。

上述装置，优选的，所述选择模块包括：

计算单元，用于对于所述子连通图中的节点对应的样本中的每一个样本，将该样本到所述子连通图中的节点对应的样本中的其它样本之间的相似度求和，得到与该样本对应的求和结果；

第二选择单元，用于选择与最大求和结果对应的样本作为初始样本。

与前一实施例相比，本实施例所选择的初始样本更加接近真实的聚类中心。

上述装置，优选的，所述生成模块包括：

初始节点选择单元，用于从所述样本集合中选择一个样本作为所述最小生成树的初始节点；

第一生成单元，用于将所述样本集合中未加入所述最小生成树的样本依次加入所述最小生成树，包括：每次将一个样本加入所述最小生成树之后，获取每一个未加入所述最小生成树的样本，与已加入所述最小生成树中的各个样本之间的相似度；确定最大相似度；将该最大相似度对应的一个未加入所述最小生成树的样本与该最大相似度对应的已加入所述最小生成树的样本相连，直至所有样本均加入到所述最小生成树。

上述装置，优选的，所述生成模块包括：

第二生成单元，用于按照两两样本之间的相似度从大到小的顺序，依次将满足预设条件的两个样本相连，直至所述样本集合中的每一个样本均与所述样本集合中的至少一个其它样本相连；

其中，两个样本满足预设条件包括：所述两个样本相连后，所有已连接的样本未构成任何回路。

附图说明

为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例或现有技术描述中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其他的附图。

图1为本发明实施提供的初始样本选择方法的一种实现流程图；

图2为本发明实施提供的原始连通图的一种示例图；

图3a-3b为本发明实施提供的图2所示原始连通图的连通子图的两种示例图；

图4a-4b为本发明实施提供的非连通子图的两种示例图；

图5为本发明实施提供的图2所示原始连通图的最小生成树的示例图；

图6为本发明实施提供的将图5所示最小生成树删除两条边后的实示例图；

图7为本发明实施提供的从每一个子连通图中的样本中选择一个样本作为初始样本的一种实现流程图；

图8为本发明实施提供的图2所示原始连通图中各个边的权重的示例图；

图9为本发明实施提供的生成最小生成树的一种过程示意图；

图10为本发明实施提供的生成最小生成树的另一种过程示意图；

图11为本发明实施提供的初始样本选择装置的一种结构示意图。

说明书和权利要求书及上述附图中的术语“第一”、“第二”、“第三”“第四”等(如果存在)是用于区别类似的部分，而不必用于描述特定的顺序或先后次序。应该理解这样使用的数据在适当情况下可以互换，以便这里描述的本申请的实施例能够以除了在这里图示的以外的顺序实施。

具体实施方式

下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有付出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。

本发明实施例提供的初始样本选择方法及装置，可以用于需要选择多个初始样本的聚类算法，如基于划分法的聚类算法。其中，基于划分法的聚类算法可以包括但不限于以下几种：K-Means算法(也叫K-均值算法)或K-Medoids算法(也叫K-中心算法)或CLARANS算法。

请参阅图1，图1为本发明实施提供的初始样本选择方法的一种实现流程图，可以包括：

步骤S11：构建样本集合中样本的原始连通图，该原始连通图中的每一个节点表征样本集合中的一个样本，原始连通图中的节点两两相连，原始连通图中任意两个节点之间边的权重为该两个节点所表征的两个样本的相似度；

样本集合即聚类算法的处理对象，也就是说，通过聚类算法对样本集合中的样本进行聚类。若样本集合中有N个样本，则原始连通图中共有N个节点，N(N-1)/2条边。

任意两个样本之间的相似度可以用该两个样本之间的欧式距离表征。两个样本之间的欧式距离越小，表示该两个样本之间的相似度越大；两个样本之间的欧氏距离越大，表示该两个样本之间的相似度越小。

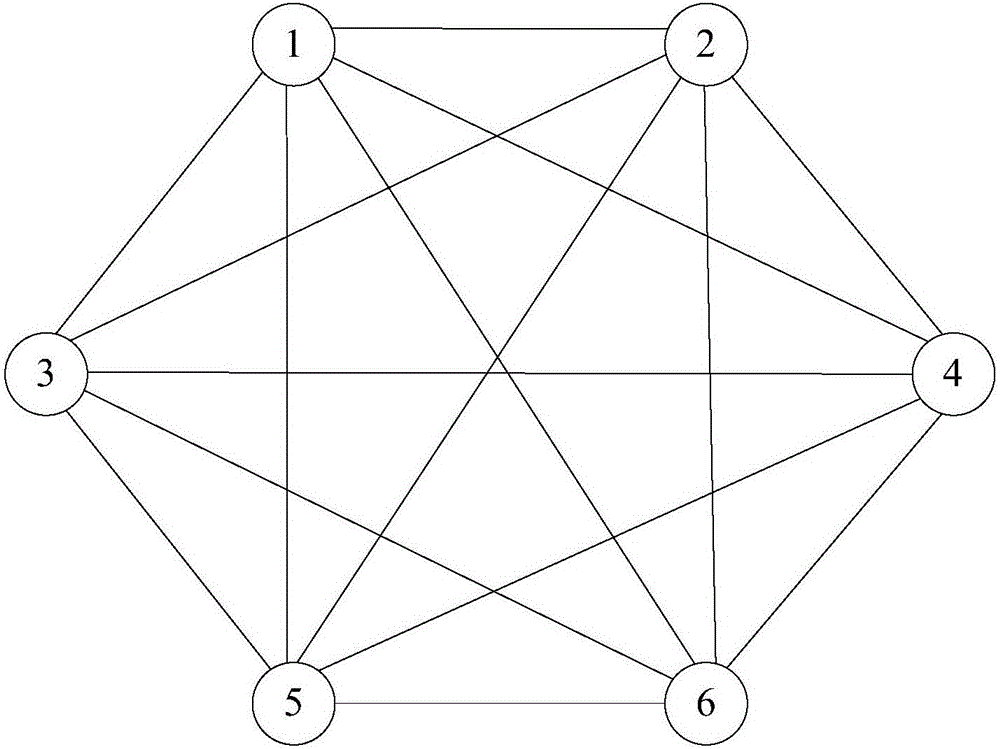
如图2所示，图2为本发明实施例提供的原始连通图的一种示例图。本示例中，假设样本集合中共有6个样本。需要说明的是，这里的样本数只是用于示例性说明，在实际应用中，样本集合中的样本的数量是远远大于6的。

步骤S12：生成上述原始连通图的最小生成树；

最小生成树中的节点数与原始连通图中的节点数相同。

一个原始连通图可以对应多个连通子图，其中，每个连通子图中节点的个数与原始连通图中节点的个数相同，每个连通子图中边的条数小于原始连通图中边的条数，且每一个节点都可以通过一定路径到达其它任何一个节点。如图3a-3b所示，为本发明实施例提供的图2所示原始连通图的连通子图的两种示例图。如图4a-4b所示，为本发明实施例提供的非连通子图的两种示例图。即图4a-4b所示的图不是图2所示原始连通图的连通子图。

而最小生成树，是原始连通图对应的所有连通子图中，边数最少，且边的权重和最大(即相似度之和最大)的一个连通子图。边的权重和最大是指在边数最少的多个连通子图中，边的权重和最大。例如，假设连通子图的边数为m时，连通子图的边数最小，则上述边数最少，且边的权重和最大的那个连通子图即为：边数为m的连通子图中，权重和最大的一个连通子图。

步骤S13：删除上述最小生成树中相似度最小的K-1条边，得到K个子连通图，K为聚类算法需要选择的初始样本的个数；

本发明实施例中，通过删除K-1条边的方式将最小生成树分割成K个子连通图，显然，每个子连通图中节点的个数小于最小生成树中节点的个数。在删除上述K-1条边时，只是将节点之间的连接关系断开，而并没有删除边所连接的两个节点，因此，上述K个子连通图的节点数之和等于上述最小生成树中的节点数。

该K个子连通图模拟了样本集合中样本的分布情况。

还以图2所示原始连通图为例，假设图2所示原始连通图的最小生成树为图5所示连通子图，共6个节点，5条边；假设聚类算法需要选择3个初始样本；假设图2中，节点1和3之间的边，以及节点1和2之间的边为5条边中相似度最小的两条边，则将该两条边删除后的示例图如图6所示。删除上述两条边后，图5所示最小生成树被分割为三个子连通图，其中，节点1构成一个子连通图，节点3和节点5构成一个子连通图，节点2，节点4和节点6构成一个子连通图。

步骤S14：从每一个子连通图中的节点对应的样本中选择一个样本作为初始样本。

从每个子连通图中的节点对应的样本中选择一个样本，获取K个初始样本。

在一可选的实施例中，可以从每一个子连通图中的节点对应的样本中随机选择一个样本作为初始样本。

以图6所示示例图为例，节点1自己构成一个子连通图，则节点1对应的样本被选为一个初始样本；从节点3和节点5中随机选择一个样本作为另一个初始样本，从节点2，节点4和节点6中随机选择一个样本作为又一个初始样本。

本发明实施例提供的初始样本选择方法，构建样本集合中样本的原始连通图，生成该原始连通图的最小生成树，根据聚类算法需要选择的初始样本个数K，以及样本之间的相似度，将最小生成树分割成K个子连通图，从每个子连通图中选择一个样本作为初始样本。本发明实施例提供的初始样本选择方法，用通过上述方法获取的K个子连通图模拟样本的分布情况，因而从K个子连通图中选择的初始样本更接近真实的聚类中心，基于本发明提供的初始样本选择方法选择的初始样本，克服了通过随机选择初始样本点导致聚类算法的收敛速度慢、聚类效果差的问题。

在一可选的实施例中，从每一个子连通图中的节点对应的样本中选择一个样本作为初始样本的一种实现流程图如图7所示，可以包括：

步骤S71：对于子连通图中的节点对应的样本中的每一个样本，将该样本到子连通图中的节点对应的样本中的其它样本之间的相似度求和，得到与该样本对应的求和结果；

步骤S72：选择与最大求和结果对应的样本作为初始样本。

需要说明的是，这里所说的求和结果最大，是指求和结果表征的相似度最大。

本发明实施例中，对于子连通图中包括至少3个节点的子连通图，可以通过图7所示实施例选择初始样本。

对于只包括一个节点的子连通图，直接将该子连通图包含的节点对应的样本选为初始样本；

对于只包括两个节点的子连通图，则从该子连通图包含的两个节点对应的两个样本中随机选择一个样本作为初始样本。

对于包括至少三个节点的子连通图，可以基于图7所示实施例选择初始样本。以图6所示包括2，4，6三个节点的子连通图为例，为便于叙述，将节点2对应的样本记为样本2，将节点4对应的样本记为样本4，将节点6对应的样本记为样本6，则从这三个样本中选择初始样本的过程为：计算样本2与样本4之间的相似度s24，以及样本2与样本6之间的相似度s26之和，得到与样本2对应的求和结果s2，s2＝s24+s26；计算样本4与样本2之间的相似度s42，以及样本4与样本6之间的相似度s46之和，得到与样本4对应的求和结果s4，s4＝s42+s46；计算样本6与样本2之间的相似度s62，以及样本6与样本4之间的相似度s64之和，得到与样本6对应的求和结果s6，s6＝s62+s64；从s2，s4和s6中确定最大值，假设为s4，则选择样本4作为一个初始样本。

在一可选的实施例中，生成原始连通图的最小生成树的一种实现方式可以为：

从样本集合中选择一个样本作为所述最小生成树的初始节点。可以从样本集合中任意选择一个样本作为最小生成树的初始节点。

将样本集合中未加入最小生成树的样本依次加入最小生成树，包括：每次将一个样本加入最小生成树之后，获取每一个未加入最小生成树的样本，与已加入最小生成树中的各个样本之间的相似度；确定最大相似度；将该最大相似度对应的一个未加入最小生成树的样本与该最大相似度对应的已加入最小生成树的样本相连，直至所有样本均加入到最小生成树。

为了便于说明，假设图2所示原始连通图中各个边的权重(即节点间的相似度)如图8所示。图8中，节点之间的相似度用欧式距离表征。则权重越小表征相似度越大。显然，在图8中，节点1与节点3之间的欧式距离为1，且最小，则节点1表征的样本点与节点3表征的样本点之间的相似度最大。假设将图8中节点1作为最小生成树的最小节点，则生成最小生成树的过程示意图如图9所示：

从2、3、4、5、6五个节点中选择与节点1之间的距离最小(即相似度最大)的节点，显然节点3与节点1之间的距离最小，则将节点3与节点1相连；

然后从2、4、5、6四个节点中选择与节点1、3之间的距离最小(即相似度最大)的节点，显然节点2与节点3之间的距离，以及节点5与节点1之间的距离最小，均为2，则从节点2和节点5中随机选择一个节点，若选择节点2，则将节点2与节点3相连，若选择节点5，则将节点5与节点1相连，假设这里选择了节点2。其中，从2、4、5、6四个节点中选择与节点1、3之间的距离最小的节点时，所计算的距离包括：节点2与节点1之间的距离，节点2与节点3之间的距离，节点4与节点1之间的距离，节点4与节点3之间的距离，节点5与节点1之间的距离，节点5与节点3之间的距离，节点6与节点1之间的距离，节点6与节点3之间的距离，然后从上述8个距离中选择最小距离。

然后从节点4、5、6三个节点中选择与节点1、2、3之间的距离最小(即相似度最大)的节点，显然节点5与节点1之间的距离最小，为2，则将节点5与节点1相连；

然后，从节点4和6两个节点中选择与节点1、2、3、5之间的距离最小的节点，显然，节点4与节点3之间的距离，以及节点6与节点1之间的距离均为3，且最小，则从节点4和6中随机选择一个节点，若选择节点4，则将节点4与节点3相连，若选择节点6，则将节点6与节点1相连，假设这里选择了节点6；

最后计算节点4到节点1、2、3、5、6之间的距离，选择与节点4之间的距离最小节点，显然，节点4与节点3之间的距离最小，则将节点4与节点3相连。至此，所有样本均已加入最小生成树。

在一可选的实施例中，生成原始连通图的最小生成树的另一种实现方式可以为：

按照两两样本之间的相似度从大到小的顺序，依次将满足预设条件的两个样本相连，直至所述样本集合中的每一个样本均与所述样本集合中的至少一个其它样本相连；

其中，两个样本满足预设条件包括：两个样本相连后，所有已连接的样本未构成任何回路。

还以图8为例，由于图8中用欧式距离表征样本之间的相似度，因此本示例中，按照两两样本之间的欧式距离从小到大的顺序，依次将满足预设条件的两个样本相连，直至样本集合中的每一个样本均与所述样本集合中的至少一个其它样本相连；具体生成最小生成树的过程示意图如图10所示：

由于节点1和节点3之间的欧氏距离最小，因此，首先将节点1和节点3相连；

然后选择欧式距离为2的边对应的节点，显然，节点1和节点5之间的欧式距离，以及节点2和节点3之间的欧式距离均为2，由于任意一组节点相连后，均不会出现回路，因此随机从中选择一组节点相连，假设选择了节点1和节点5相连；

然后，选择欧式距离为3的边对应的节点，显然，节点1与节点6之间的欧式距离，节点2与节点5之间的欧式距离，以及节点3与节点4之间的欧式距离均为3，由于任意一组节点相连后，均不会出现回路，因此随机从中选择一组节点相连，假设选择了节点2和节点5相连；

然后，选择选择欧式距离为4的边对应的节点，显然，节点1与节点4之间的欧式距离，节点2与节点6之间的欧式距离，节点3与节点6之间的欧式距离，以及节点4与节点5之间欧式距离均为4，由于任意一组节点相连后，均不会出现回路，因此随机从中选择一组节点相连，假设选择了节点2和节点6相连；

然后，选择选择欧式距离为5的边对应的节点，显然，节点1与节点2之间的欧式距离，节点2与节点4之间的欧式距离，节点3与节点5之间的欧式距离，以及节点4与节点6之间欧式距离，以及节点5与节点6之间的欧式距离均为5，由于节点1与节点2相连后，节点1、节点2和节点5会构成回路，节点3与节点5相连后，节点1、节点3和节点5也会构成回路，节点5和节点6相连后，也会构成回来，因此只能从节点2和4，以及节点4和6中选择选择一组节点相连，假设选择了节点4和节点6相连；至此，所有样本均已加入最小生成树。

与方法实施例相对应，本发明实施例还提供一种初始样本选择装置。本发明实施例提供的初始样本选择装置的一种结构示意图如图11所示，可以包括：

构建模块111，生成模块112，删除模块113和选择模块114；其中，

构建模块111用于构建样本集合中样本的原始连通图；该原始连通图中的每一个节点表征样本集合中的一个样本，原始连通图中的节点两两相连，原始连通图中任意两个节点之间边的权重为该两个节点所表征的两个样本的相似度；

生成模块112用于生成原始连通图的最小生成树；

删除模块113用于删除最小生成树中相似度最小的K-1条边，得到K个子连通图，K为聚类算法需要选择的初始样本的个数；

选择模块114用于从每一个子连通图中的节点对应的样本中选择一个样本作为初始样本。

本发明实施例提供的初始样本选择装置，构建样本集合中样本的原始连通图，生成该原始连通图的最小生成树，根据聚类算法需要选择的初始样本个数K，以及样本之间的相似度，将最小生成树分割成K个子连通图，从每个子连通图中选择一个样本作为初始样本。本发明实施例提供的初始样本选择装置，用通过上述方法获取的K个子连通图模拟数据的分布情况，因而从K个子连通图中选择的初始样本更接近真实的聚类中心，基于本发明提供的初始样本选择装置选择的初始样本，克服了通过随机选择初始样本点导致聚类算法的收敛速度慢、聚类效果差的问题。

在一可选的实施例中，选择模块114可以包括：

第一选择单元，用于从每一个子连通图中的节点对应的样本中，随机选择一个样本作为初始样本。

在一可选的实施例中，选择模块114可以包括：

计算单元，用于对于子连通图中的节点对应的样本中的每一个样本，将该样本到子连通图中的节点对应的样本中的其它样本之间的相似度求和，得到与该样本对应的求和结果；

第二选择单元，用于选择与最大求和结果对应的样本作为初始样本。

在一可选的实施例中，生成模块112可以包括：

初始节点选择单元，用于从样本集合中选择一个样本作为最小生成树的初始节点；

第一生成单元，用于将样本集合中未加入最小生成树的样本依次加入最小生成树，包括：每次将一个样本加入最小生成树之后，获取每一个未加入最小生成树的样本，与已加入最小生成树中的各个样本之间的相似度；确定最大相似度；将该最大相似度对应的一个未加入最小生成树的样本与该最大相似度对应的已加入最小生成树的样本相连，直至所有样本均加入到最小生成树。

在一可选的实施例中，生成模块112可以包括：

第二生成单元，用于按照两两样本之间的相似度从大到小的顺序，依次将满足预设条件的两个样本相连，直至样本集合中的每一个样本均与样本集合中的至少一个其它样本相连；

其中，两个样本满足预设条件包括：两个样本相连后，所有已连接的样本未构成任何回路。

本领域普通技术人员可以意识到，结合本文中所公开的实施例描述的各示例的单元及算法步骤，能够以电子硬件、或者计算机软件和电子硬件的结合来实现。这些功能究竟以硬件还是软件方式来执行，取决于技术方案的特定应用和设计约束条件。专业技术人员可以对每个特定的应用来使用不同方法来实现所描述的功能，但是这种实现不应认为超出本发明的范围。

所属领域的技术人员可以清楚地了解到，为描述的方便和简洁，上述描述的系统(若存在)、装置和单元的具体工作过程，可以参考前述方法实施例中的对应过程，在此不再赘述。

在本申请所提供的几个实施例中，应该理解到，所揭露的系统、装置和方法，可以通过其它的方式实现。例如，以上所描述的装置实施例仅仅是示意性的，例如，所述单元的划分，仅仅为一种逻辑功能划分，实际实现时可以有另外的划分方式，例如多个单元或组件可以结合或者可以集成到另一个系统，或一些特征可以忽略，或不执行。另一点，所显示或讨论的相互之间的耦合或直接耦合或通信连接可以是通过一些接口，装置或单元的间接耦合或通信连接，可以是电性，机械或其它的形式。

所述作为分离部件说明的单元可以是或者也可以不是物理上分开的，作为单元显示的部件可以是或者也可以不是物理单元，即可以位于一个地方，或者也可以分布到多个网络单元上。可以根据实际的需要选择其中的部分或者全部单元来实现本实施例方案的目的。

另外，在本发明各个实施例中的各功能单元可以集成在一个处理单元中，也可以是各个单元单独物理存在，也可以两个或两个以上单元集成在一个单元中。

所述功能如果以软件功能单元的形式实现并作为独立的产品销售或使用时，可以存储在一个计算机可读取存储介质中。基于这样的理解，本发明的技术方案本质上或者说对现有技术做出贡献的部分或者该技术方案的部分可以以软件产品的形式体现出来，该计算机软件产品存储在一个存储介质中，包括若干指令用以使得一台计算机设备(可以是个人计算机，服务器，或者网络设备等)执行本发明各个实施例所述方法的全部或部分步骤。而前述的存储介质包括：U盘、移动硬盘、只读存储器(ROM，Read-Only Memory)、随机存取存储器(RAM，Random Access Memory)、磁碟或者光盘等各种可以存储程序代码的介质。

对所公开的实施例的上述说明，使本领域专业技术人员能够实现或使用本发明。对这些实施例的多种修改对本领域的专业技术人员来说将是显而易见的，本文中所定义的一般原理可以在不脱离本发明的精神或范围的情况下，在其它实施例中实现。因此，本发明将不会被限制于本文所示的这些实施例，而是要符合与本文所公开的原理和新颖特点相一致的最宽的范围。