最小间距可控的超宽带无栅瓣稀疏线阵设计方法与流程

本发明涉及天线，尤其是涉及一种最小间距可控的超宽带无栅瓣稀疏线阵设计方法。

背景技术：

随着电子技术的飞速发展和宽带通信设备的出现，天线的超宽带技术也在不断发展。超宽带天线可以实现宽带信号的瞬时接收，且可以为不同功能系统共享使用，在通信、导航、雷达中具有较为广泛的应用[1,2]。在不同应用下超宽带有不同的定义，本发明中对超宽带的定义指的是频域的带宽比值不小于3︰1。稀疏阵列是指阵元位置不再以半波长等间距均匀分布，而是按照某种规则进行不等间距分布，其具有波束窄、空间角分辨率高、能减弱阵元间互耦等特点，这些优点使得稀疏阵列天线颇具实用性，在雷达、声纳系统等中具有重要作用[3]。众所周知，按照传统方法设计等间隔超宽带阵列时，频率增大时电尺寸也会不断增大，最终导致在高频段时产生栅瓣问题[4,5]；而如果采用稀疏阵列布局技术，则可以在一定程度上降低栅瓣电平。由于实际工程中的单元天线总是具有一定的物理尺寸，因此稀疏阵列设计通常需满足最小间距的设计要求。

关于稀疏阵列的研究有很多，文献[6]中提出了一种基于凸优化实现阵列稀疏化的方法，两个优化目标分别是最大程度降低峰值副瓣电平和最大化稀疏度，相对于阵元数目相同的均匀线阵，该稀疏线阵具有更低的峰值副瓣电平和更窄的主瓣宽度，但该方法并未涉及到宽带的性能。中国专利CN201410419309.4公开了一种阵列天线辐射场和散射场综合低副瓣快速实现方法[7]，该专利先对均匀阵列优化得到初始稀疏排布方案，再计算和对比阵列天线的辐射场和散射场的最大副瓣电平，当同时满足低副瓣要求则得到优化结果，否则通过交叉和变异的方法更新阵列天线稀疏排布矩阵，该专利不足之处在于并未涉及到宽带性能，该阵列在超宽带频率范围工作时存在出现栅瓣的问题。另外，中国专利CN201510770122.3公开了一种基于地理空间约束的稀疏天线阵列的优化布阵方法[3]，控制了最小间距，但同样也没有实现超宽带性能，其栅瓣/副瓣区域峰值电平也较高。

稀疏阵列设计方法提供了实现期望副瓣电平的可能性，但更多是在窄带范围内布局，对副瓣及栅瓣电平的抑制也较弱。在[8]中，均匀激励的阵元随机分布在指定的孔径上，该方法不能保证阵元有足够的间距或者严格满足旁瓣电平的要求。在[9]中研究了在有限带宽上使用多个给定方向图的小阵列来合成所需的阵列以及方向图。后来，基于分形概念已经设计出多频带阵列以及对带宽相当不敏感但旁瓣电平抑制能力有限的阵列配置[10-13]。还有一些阵列设计方法只能在窄带或者有限扫描范围内抑制副瓣电平和实现方向图控制[14-17]。在[18]中使用了阵元数目相对较少(例如8或16个阵元)的扫描阵列，对阵元进行简单扰动而得到优化。波束扫描可以被认为是增加带宽；波束控制在可见区域操作阵因子，带宽增加时阵因子被压缩到可见区域；在窄带阵列设计中，这两个方法都可能导致栅瓣的出现[19,20]。

近年来，许多研究者开始尝试在更宽的频率范围内合成无栅瓣/低副瓣宽带阵列方向图，许多全局优化方法得到较为广泛的应用[21-24]，但是对于大型的阵列天线综合而言，全局优化法计算量偏大，收敛速度较慢。超宽带线性、平面和体积阵列设计通过将优化方法与阵列表示技术相结合，例如分形、非周期分割和其他数学结构，这些方法使得所设计阵列的方向图在很宽的频率范围内拥有很低的峰值副瓣电平，而且得到阵元数目少、窄波束、大带宽和相对低的成本的大孔径稀疏阵列。目前已经成功地使用分形技术[25-27]和升幂级数[28]来设计有效的超宽带稀疏线性阵列，这些方法对于设计包含从一百到几千个元素的线性阵列布局最有用。分形技术引入连接因子来控制分形发生器“树”在迭代构建过程中如何相互应用，分形“树”末端(分支的尖端)的几何形状决定了阵列布局。这种设计优化技术已经被证明，对于设计中型到非常大尺寸的超宽带阵列是非常有效的，甚至可以多达数千个元件。在[28]中基于升幂级数表示的阵列非常类似于分形结构，其中不断重复地用优化的子阵列替换原阵列中的元素以生成更大的阵列，解决了均匀线阵在高频段产生栅瓣的问题，在带宽很宽的工作波段内栅瓣/副瓣区域的峰值电平基本保持不变。但是该方法得到的最小间距大于低频半波长的101元或以下超宽带阵列的峰值副瓣/栅瓣电平仅为-10db左右，无法满足通常工程应用的需求。因此，在此基础上进一步优化阵元位置分布以降低阵列峰值副瓣/栅瓣电平，则显得尤为重要。

参考文献：

[1]张志亚.宽带天线及波束赋形阵列天线研究[D].西安电子科技大学,2012.

[2]陈立甲等.超宽带天线:中国,201510560304.8[P].2015-12-23.

[3]崔国龙等.一种基于地理约束的稀疏天线阵列的优化布阵方法:中国201510770122.3[P].2016-03-16.

[4]罗天光.大间距相控阵天线栅瓣抑制方法研究[D].电子科技大学,2014.

[5]潘敏.线形阵列栅瓣的抑制[J].大众科技,2009(12):32-33.

[6]Cen L,Ser W,Cen W,et al.Linear sparse array synthesis via convex optimization[C]//Proceedings of 2010IEEE International Symposium on Circuits and Systems.IEEE,2010:4233-4236.

[7]王从思等.一种阵列天线辐射场和散射场综合低副瓣快速实现方法:中国专利CN201410419309.4[P].2014-12-03.

[8]Lo Y.A mathematical theory of antenna arrays with randomly spaced elements[J].IEEE Transactions on Antennas and Propagation,1964,12(3):257-268.

[9]King D,Packard R,Thomas R.Unequally-spaced,broad-band antenna arrays[J].IEEE Transactions on Antennas and Propagation,1960,8(4):380-384.

[10]Kim Y,Jaggard D L.The fractal random array[C]//IEEE Proceedings.1986,74:1278-1280.

[11]Puente-Baliarda C,Pous R.Fractal design of multiband and low side-lobe arrays[J].IEEE Transactions on Antennas and Propagation,1996,44(5):730.

[12]Werner D H,Gingrich M A,Werner P L.A self-similar fractal radiation pattern synthesis technique for reconfigurable multiband arrays[J].IEEE Transactions on Antennas and Propagation,2003,51(7):1486-1498.

[13]Werner D H,Ganguly S.An overview of fractal antenna engineering research[J].IEEE Antennas and propagation Magazine,2003,45(1):38-57.

[14]Jin N,Rahmat-Samii Y.Advances in particle swarm optimization for antenna designs:Real-number,binary,single-objective and multiobjective implementations[J].IEEE Transactions on Antennas and Propagation,2007,55(3):556-567.

[15]Haupt R L.Thinned arrays using genetic algorithms[J].IEEE Transactions on Antennas and Propagation,1994,42(7):993-999.

[16]Weile D S,Michielssen E.Integer coded Pareto genetic algorithm design of constrained antenna arrays[J].Electronics Letters,1996,32(19):1744-1745.

[17]Ares-Pena F J,Rodriguez-Gonzalez J A,Villanueva-Lopez E,et al.Genetic algorithms in the design and optimization of antenna array patterns[J].IEEE Transactions on Antennas and Propagation,1999,47(3):506-510.

[18]Bray M G,Werner D H,Boeringer D W,et al.Optimization of thinned aperiodic linear phased arrays using genetic algorithms to reduce grating lobes during scanning[J].IEEE Transactions on antennas and propagation,2002,50(12):1732-1742.

[19]Petko J S,Werner D H.The pareto optimization of ultrawideband polyfractal arrays[J].IEEE Transactions on Antennas and Propagation,2008,56(1):97-107.

[20]Doles J H,Benedict F D.Broad-band array design using the asymptotic theory of unequally spaced arrays[J].IEEE transactions on antennas and propagation,1988,36(1):27-33.

[21]Rocca P,Benedetti M,Donelli M,et al.Evolutionary optimization as applied to inverse scattering problems[J].Inverse Problems,2009,25(12):123003.

[22]Rocca P,Oliveri G,Massa A.Differential evolution as applied to electromagnetics[J].IEEE Antennas and Propagation Magazine,2011,53(1):38-49.

[23]Robinson J,Rahmat-Samii Y.Particle swarm optimization in electromagnetics[J].IEEE transactions on antennas and propagation,2004,52(2):397-407.

[24]Goudos S K,Siakavara K,Samaras T,et al.Self-adaptive differential evolution applied to real-valued antenna and microwave design problems[J].IEEE Transactions on Antennas and Propagation,2011,59(4):1286-1298.

[25]Petko J S,Werner D H.The evolution of optimal linear polyfractal arrays using genetic algorithms[J].IEEE transactions on antennas and propagation,2005,53(11):3604-3615.

[26]Petko J S,Werner D H.An autopolyploidy-based genetic algorithm for enhanced evolution of linear polyfractal arrays[J].IEEE transactions on antennas and propagation,2007,55(3):583-593.

[27]Petko J S,Werner D H.Interleaved ultrawideband antenna arrays based on optimized polyfractal tree structures[J].IEEE Transactions on Antennas and Propagation,2009,57(9):2622-2632.

[28]Gregory M D,Werner D H.Ultrawideband aperiodic antenna arrays based on optimized raised power series representations[J].IEEE Transactions on Antennas and Propagation,2010,58(3):756-764.

技术实现要素：

本发明的目的在于针对现有技术中存在的上述不足，提供最小间距可控的超宽带无栅瓣稀疏线阵，而且有较低的峰值副瓣电平；在保证宽频带内栅瓣/副瓣区域的峰值电平基本保持不变的前提下，还可以最大程度降低栅瓣/副瓣区域的峰值电平；相对于一些算法如遗传算法等，基于迭代凸优化的数值微扰优化法优化速度明显加快的最小间距可控的超宽带无栅瓣稀疏线阵设计方法。

本发明包括以下步骤：

1)假设在天线阵列的布阵范围为[-D/2,D/2]上布置了2N+1个阵元，位置为d_-N，d_-(N-1)，...，d₀，d₁，...，d_N-1，d_N，其中d_-N＝-D/2，d_N＝D/2，为阵列的孔径大小，对于任何宽带天线单元激励等幅同相的阵列，当天线系统的工作波段在一倍频至三倍频(f₀～3f₀，对应的波长为)时，此波段内栅瓣/副瓣区域的峰值电平基本保持不变(误差小于0.5dB)。具体步骤如下：

(1)对于一个沿Z轴均匀分布并且关于原点对称的线阵，它的阵因子公式为

其中，β表示自由空间波数，d是阵元间距为表示求和运算符，θ表示从X轴观测的角度，已知均匀阵列在高频波段会生成栅瓣，为了抑制栅瓣生成，对阵元位置进行初步优化；

(2)将式(1)中的n变为n^r，并引入一个新的参数ξ，该参数由式(2)确定，新的d_n由式(3)给出，得到的新阵列为RPS阵，它的阵因子表达式为式(4)：

d_n＝sign(n)d_minξ|n|^r,|n|≤N (3)

其中，d_min为λ₀/2(低频时的半个波长)，选取合适的r和N，使得天线系统工作在波段f₀～3f₀时，栅瓣/副瓣区域的峰值电平基本保持不变。

2)为了进一步降低栅瓣/副瓣区域的峰值电平，采用多步数值微扰优化法。所述多步数值微扰优化法的具体步骤为：将式(4)中阵元位置d_n(n＝0,1,2,…N)变成d_n+Δ_n，Δ_n代表每一个阵元的位置微扰量，由于这个约束条件，微扰后的阵因子式可以表达为式(5)：

其中，AF(θ)是微扰前的阵因子式，是一步位置微扰后产生的变化量；

微扰时保证满足最小间距约束、位置微扰幅度约束两个条件，对以上线性阵列的阵元位置进行微扰，具体约束条件如下：

(1)最小间距约束：在实际天线阵布局过程中，阵元间距需不小于所设计的单元天线尺寸，因此在微扰过程中，需要满足最小间距约束d_n-d_n-1≥d_min，d_min为λ₀/2，n＝0,1,2,…N；

(2)位置微扰幅度约束：为了保证位置微扰的近似精度，要求即对于n＝0,1,2,…N，均满足|βΔ_n|≤μ，此处的μ的大小决定了位置微扰的幅度；

遵循以上约束条件，采用迭代二阶锥规划法对RPS阵进行多步位置微扰优化，在每一步微扰，二阶锥规划法的优化目标是最小化栅瓣/副瓣区域的峰值电平；多步微扰后，当栅瓣/副瓣区域的峰值电平基本保持不变且阵列布局也保持不变时，得到最优化阵列布局结果。

本发明的基本思路是：首先，解析法设计超宽带稀疏线阵；然后通过多步位置微扰，进一步优化解析法设计的RPS阵，使得栅瓣/副瓣区域的峰值电平大大降低。在整个优化布局的过程中，最小间距始终可控。

与现有技术相比，本发明的有益效果在于：解析法与数值法相结合，解决了稀疏阵列在宽频带波段工作时，会产生栅瓣以及较高峰值副瓣的问题，并最大程度的降低栅瓣/副瓣区域峰值电平；在至少三倍频的波段范围内栅瓣/副瓣区域峰值电平基本保持不变，在整个过程中最小间距可控。

附图说明

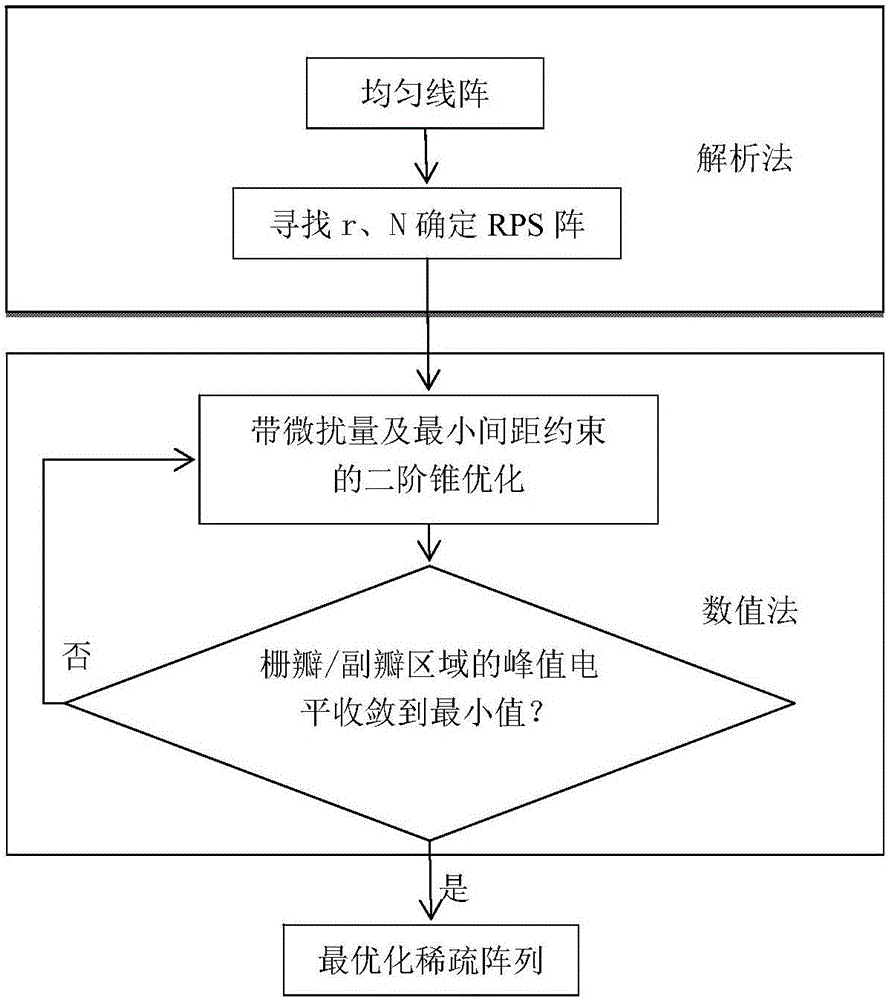
图1为本发明的技术方案流程图。

图2为不同r、N值下的栅瓣/峰值副瓣电平。

图3为初始RPS阵在3GHz时的阵因子图。

图4为最优化稀疏阵列在3GHz时的阵因子图。

图5为优化布局过程中的峰值副瓣电平图。

图6为优化布局过程中正半轴的阵元位置图mark。

图7为最优化稀疏阵列频率1GHz下的阵因子图。

图8为最优化稀疏阵列频率1.5GHz下的阵因子图。

图9为最优化稀疏阵列频率2GHz下的阵因子图。

图10为最优化稀疏阵列频率2.5GHz下的阵因子图。

图11为最优化稀疏阵列频率3GHz下的阵因子图。

具体实施方式

本发明提出的最小间距可控的超宽带无栅瓣稀疏线阵设计方法分为两步，如图1所示：第一步，解析法设计的RPS阵，确定了超宽带稀疏线阵；第二步，多步数值微扰优化上述阵列的阵元位置得到更低栅瓣/峰值副瓣电平的最小间距可控的超宽带稀疏线阵。图1为本发明的技术流程图。

下面结合一个实例对本发明做进一步解释。设计目标：频率范围在1GHz～3GHz之间，栅瓣/副瓣区域的峰值电平保持不变的超宽带无栅瓣稀疏线阵。

按下面步骤实施：

步骤1：假设在天线阵列的布阵范围为上布置了个激励等幅同相的宽带天线阵元，位置为d_-N，d_-(N-1)，...，d₀，d₁，...，d_N-1，d_N，其中d_-N＝-D/2，d_N＝D/2。

步骤1-1：对于一个均匀分布的周期线阵，在笛卡尔坐标系中，2N+1个阵元沿Z轴关于原点对称分布，此周期阵列的阵因子幂级数表达式为

其中，从X轴观测的角度θ为[0°,90°]，采样密度Δ_θ是0.02°，阵元间距d为0.15m(低频(1GHz)时的半个波长)，β是自由空间的波数。已知均匀阵列在高频波段会生成栅瓣，为了抑制栅瓣，下一步将对上述阵列进行初步优化。

步骤1-2：将式(6)中的变为n^r，并引入一个新的参数ξ，该参数由式(7)确定，新的d_n由式(8)给出，得到RPS阵，它的阵因子表达式为式(9)。

d_n＝sign(n)d_minξ|n|^r,|n|≤N (8)

其中，d_min为0.15m(低频(1GHz)时的半个波长)。为了避免过度稀疏化，r值不可选取的过大或过小，因此0.75≤r≤1.25。为了选取合适的r、N值，由图2得知，当r取0.81、N取50时，栅瓣/峰值副瓣电平在三倍频的频率范围内基本保持不变，因此我们得到了解析法解出的超宽带无栅瓣线阵。在图3中，读出此时的峰值副瓣电平为-9.4263dB。

步骤2：在高频3GHz时，采用多步数值微扰优化法对阵元位置微扰来进一步降低栅瓣/副瓣区域的峰值电平。将式(9)中阵元位置d_n(n＝0,1,2,…N)变成d_n+Δ_n，Δ_n代表每一个阵元的位置微扰量，为了保证位置微扰的近似精度有微扰后的阵因子式可以表达为式(10)：

其中，AF(θ)是微扰前的阵因子式，是一步位置微扰后产生的变化量。

微扰时保证满足最小间距约束、位置微扰幅度约束两个条件，对以上线性阵列的阵元位置进行微扰，具体约束条件如下：

(1)最小间距约束：在实际天线阵布局过程中，阵元间距需不小于所设计的单元天线尺寸，因此在微扰过程中，需要满足最小间距约束d_n-d_n-1≥d_min，d_min为λ₀/2，n＝0,1,2,…N。

(2)位置微扰幅度约束：为了保证位置微扰的近似精度，要求即对于n＝0,1,2,…N，均满足|βΔ_n|≤μ，此处的μ的大小决定了位置微扰的幅度。本例中μ为π/5，相对于工作波长位置微扰为1/10。

遵循以上约束条件，采用迭代二阶锥规划法对RPS阵进行多步位置微扰优化。在每一步微扰，二阶锥规划法的优化目标是最小化栅瓣/副瓣区域的峰值电平。多步微扰后，当栅瓣/副瓣区域的峰值电平基本保持不变且阵列布局也保持不变时，得到最优化阵列布局结果。图4是最终优化稀疏阵列在3GHz时的阵因子图，此时的栅瓣/副瓣区域的峰值电平为-14.6514dB。本例中栅瓣/副瓣区域的峰值电平总共降低了5.2251dB。

图5给出了每步微扰结果的栅瓣/副瓣区域的峰值电平值，大约100次迭代后，栅瓣/副瓣区域的峰值电平降到大约-14.6514dB，随后基本保持不变。图6给出了优化布局过程中部分次阵元位置布局图，由于阵元关于原点对称分布，这里仅画出正半轴的阵元。可以看出多步微扰后，阵列布局保持不变。图7～11给出了5个不同频率(1GHz、1.5GHz、2GHz、2.5GHz和3GHz)下的阵因子图，它们的栅瓣/副瓣区域的峰值电平分别为-14.65dB、-14.63dB、-14.65dB、-14.65dB、-14.65dB，在误差不超过0.5dB时，该结果可以认定为基本保持不变。