一种电池储能系统典型工况的评估方法与流程

本发明涉及一种典型工况的评估方法，具体涉及一种电池储能系统典型工况的评估方法。

背景技术：

近些年，我国风能和大阳能发电快速发展，电池储能电站的规模不断扩大，电池储能电站采集上来的储能电池数据也日益剧增，已运行的十MW级电池储能电站的电池单体数量已达数十万，储能电池数据的使用价值是巨大的，尚未充分挖掘。

目前对于储能系统充放功率的研究都集中于优化控制与容量配置等方面，对于典型工况曲线的挖掘及获取工作关注较少。目前关于典型工况曲线挖掘的研究主要集中在电动汽车\混合电动汽车上。例如通过求出电池功率的分布函数和概率分布，然后随机产生电池充放电功率的典型工况曲线挖掘方法。但该方法随机产生电池的充放电功率，仅考虑典型工况曲线与实际工况曲线在概率分布上的一致性，未考虑典型工况曲线与实际工况曲线在具体时刻取值的一致性，使得典型工况曲线与实际工况曲线在时间序列上差别较大。因此不适用于电力系统，特别是电力储能系统的工况分析与提炼。

技术实现要素：

为了克服上述现有技术的不足，本发明提供一种电池储能系统典型工况的评估方法，本发明实现了对电池储能系统典型工况的分析与评估，验证其有效性。

为了实现上述发明目的，本发明采取如下技术方案：

一种电池储能系统典型工况的评估方法，所述方法包括如下步骤：

(1)采用主成分分析方法提取电池样本数据特征矩阵的主要成分，并根据计算每个特征对主成分的贡献提取代表数据属性的主要特征因子；

(2)采用相关系数计算方式，通过分析样本与典型工况数据主要特征参数的相似性，评估典型工况的性能。

优选的，所述步骤(1)包括如下步骤：

步骤1-1、根据待分析数据特性设计数据的特征参数；

步骤1-2、设样本数量为M，特征参数数量为N，计算每个样本的每个特征参数，构成M*N参数矩阵P，P中每个参数为样本的特征；

步骤1-3、对所述参数矩阵进行主成分分析。

优选的，所述步骤1-1中，所述特征参数包括：样本最大值、样本最小值、样本幅值、样本平均值、样本非0值区间均值、样本标准偏差、一阶导最小值、一阶导最大值、一阶导标准偏差、数据增长区间比例、数据减小区间比例、数据平稳区间比例、数据0值区间比例。

优选的，所述步骤1-3中包括如下步骤：

步骤1-3-1、使用主成分分析法提取所述参数矩阵P的主成分，设置参数α，选取得分超过α的成分为主成分；

步骤1-3-2、根据各特征参数的负荷矩阵，设置参数β，选取负荷矩阵中对主成分贡献大于β的特征参数作为样本数据的主要特征因子，记特征因子个数为n，因此所有样本会形成M个n维向量。

优选的，所述步骤(2)中，采用皮尔逊相关系数计算的方式计算样本数据与典型工况数据特征参数的相关系数，包括如下步骤：

步骤2-1、计算典型工况数据与所有样本主要特征因子的相关系数；

步骤2-2、分析相关系数结果评估典型工况数据性能。

优选的，所述步骤2-1包括如下步骤：

步骤2-1-1、根据特征因子分析模块得到的主要特征因子，对典型工况及每一个样本计算特征因子数据；

步骤2-2-2、计算每一个样本特征因子与典型工况特征因子的相关系数，相关系数计算方法可以采用皮尔逊相关系数计算方法，计算公式为：

式中，r是相关系数计算结果，n是特征参数个数，x是样本数据特征因子，y是典型工况数据特征因子。

优选的，所述步骤2-2中，包括如下步骤：

步骤2-2-1、设置相关系数阈值α和比例阈值β；

步骤2-2-2、统计所有样本与典型工况相关系数超过α的比例，若大于β则认为典型工况数据有效，能代表实际工程数据的典型工作模式；否则认为典型工况数据无效。

与最接近的现有技术比，本发明提供的技术方案具有以下优异效果：

本发明通过主成分分析及相关系数计算对电池数据典型工况进行分析评估，其中主成分分析方法提取数据的重要特征，相关系数计算可以分析典型工况数据与样本数据特征的相似性，从而评估典型工况数据的性能。

本发明具有通用性和可复制性,可推广应用于储能系统参与跟踪发电计划，参与系统调频,削峰填谷等不同应用模式下确定的储能系统充放电功率分析及其典型运行工况曲线的提取、评估以及复验等。

附图说明

图1是一种电池储能系统典型工况的评估方法流程图，

图2是一种电池储能系统运行工况的特征因子分析方法流程图，

图3是一种典型工况数据性能分析方法流程图。

具体实施方式

下面结合附图对本发明作进一步详细说明。

如图1所示，本发明实施例提供了一种电池储能系统典型工况的评估方法，其包括特征因子分析模块和典型工况性能分析模块，分析方法步骤如下：

步骤1设计样本数据特征参数，依据数据类型设计能代表数据属性的特征参数。

步骤2对每个样本计算其特征参数。

步骤3对特征参数矩阵进行主成分分析，计算每个特征参数对主成分的贡献，从而提取可以代表数据属性的主要特征因子。

步骤4计算典型工况数据与所有样本主要特征因子的相关系数。

步骤5分析相关系数结果评估典型工况数据性能。

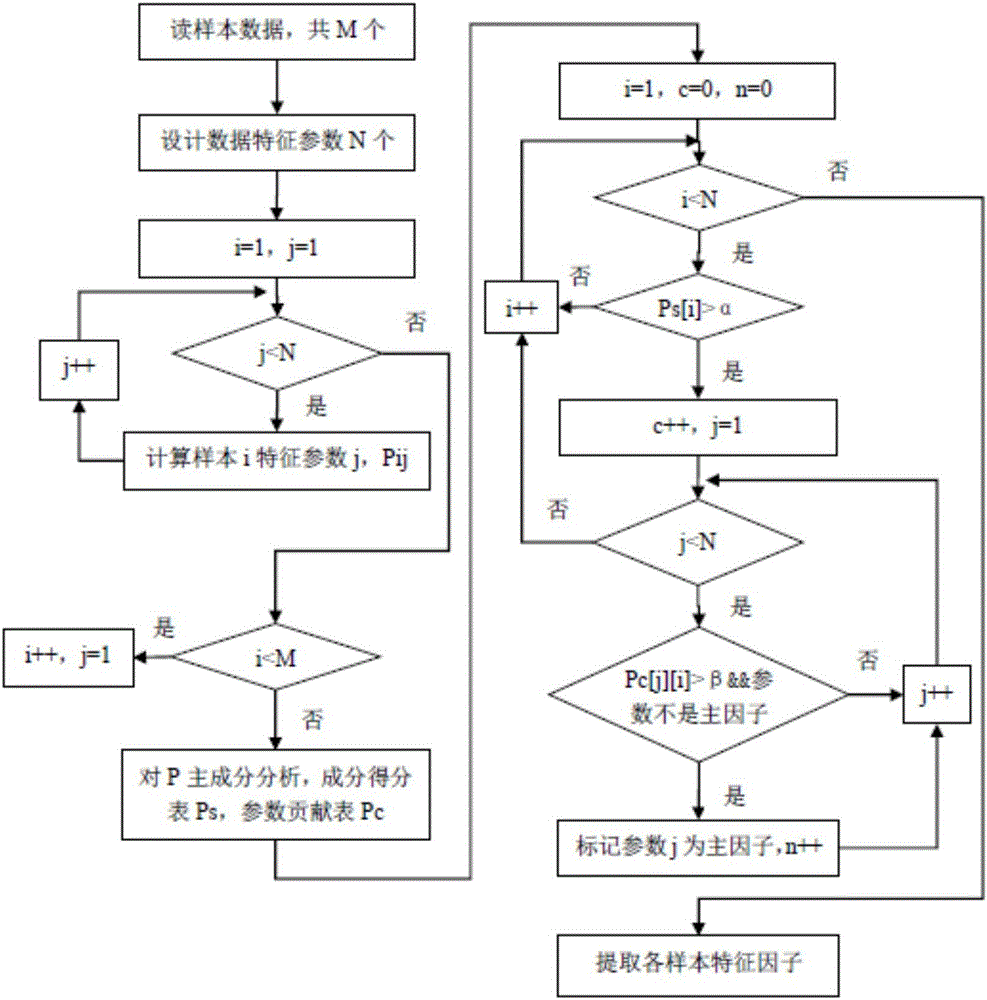
如图2所示，本发明实施例提供了一种电池储能系统运行工况的特征因子分析方法，包括如下步骤：

步骤1根据待分析数据特性设计数据的特征参数，如样本最大值、样本最小值、样本幅值、样本平均值、样本非0值区间均值、样本标准偏差、一阶导最小值、一阶导最大值、一阶导标准偏差、数据增长区间比例、数据减小区间比例、数据平稳区间比例、数据0值区间比例等特征参数。

步骤2样本数量记为M，特征参数数量极为N，计算每个样本的每个特征参数，构成M*N参数矩阵P，P中每个参数(即各个样本的各个特征)计算方法的依据为步骤1-1特征设计方法，表达式如下：

步骤3使用主成分分析方法提取矩阵P的主成分，设置参数α，选取得分超过α的成分为主成分。

步骤4根据各特征参数的负荷矩阵，设置参数β，选取负荷矩阵中对主成分贡献大于β的特征参数作为样本数据的主要特征因子，记特征因子个数为n，因此所有样本会形成M个n维向量。如下表所示为某电池SOC跟踪数据特征参数负荷矩阵，表中加粗和下划线标记了主要特征因子，共5个。

如图3所示，本发明实施例提供了一种典型工况数据性能分析方法，包括如下步骤：

步骤1根据特征因子模块分析得到的结果计算典型工况数据及各样本的特征因子。

步骤2计算每一个样本特征因子与典型工况特征因子的相关系数，相关系数计算方法可以采用皮尔逊相关系数计算方法，计算公式为：

其中r是相关系数计算结果，n是特征参数个数，x是样本数据特征因子，y是典型工况数据特征因子。

(3)设置相关系数阈值α和比例阈值β，统计所有样本与典型工况相关系数超过α的比例，如果大于β则认为典型工况数据有效，能代表实际工程数据的典型工作模式；否则认为典型工况数据无效。

最后应当说明的是：以上实施例仅用以说明本发明的技术方案而非对其限制，尽管参照上述实施例对本发明进行了详细的说明，所属领域的普通技术人员应当理解：依然可以对本发明的具体实施方式进行修改或者等同替换，而未脱离本发明精神和范围的任何修改或者等同替换，其均应涵盖在本发明的权利要求范围当中。