基于EWT‑ESN的短期风电功率预测方法与流程

本发明涉及风电输出功率预测
技术领域：
，是一种基于EWT-ESN的短期风电功率预测方法。
背景技术：
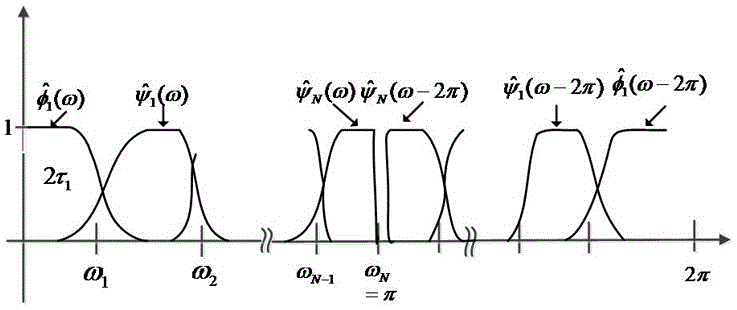
：目前，风力发电技术的快速发展使得风机装机容量在地区电力系统中所占的比例逐渐增长，然而风电输出功率受风力间歇性、波动性的影响极不稳定，大规模风电并网给电力系统调度部门以及电能供应的可靠性带来了挑战，因此，准确而可靠地风电输出功率预测具有重要的意义。风能的随机性和间歇性特点导致风电输出功率表现为波动强烈的非线性时间序列，目前，包括神经网络和SVM在内很多计算智能预测方法，能从风电功率的历史时间序列中描述出输入与输出的非线性关系，已经在风电功率预测方面得到了广泛的应用；然而，这些采用智能化算法直接建模的单一预测方法由于缺乏对风电功率本身变化规律的把握，很难从本质上取得较高的预测精度，往往会在风电功率变化剧烈的预测点产生较大的误差。近年来经验模态分解(EmpiricalModeDecomposition,EMD)和小波分析结合神经网络和SVM的各种组合预测方法在风电功率预测方面取得了成功的应用，实验结果证明与单一预测方法相比，组合预测方法可以有效的提高预测精度。EMD是近年来由NordenE.Huang在处理非线性，非平稳性信号方面得到了广泛的应用，然而，EMD缺乏严格的理论支撑，且其过包络和欠包络等问题易导致模态混叠现象，进而会导致分解得到较多的虚假模态分量，不仅影响分解结果的有效性，同时增加了组合预测的计算规模。在EMD的基础上，通过构造合适的正交小波滤波器组对信号的傅里叶谱进行自适应划分，以提取具有紧支撑傅里叶频谱的AM-FM成分。EWT是以小波分析为理论框架建立的，其计算速度优于EMD方法且具有较强的鲁棒性。回声状态网络(echostatenetworks,ESN)作为一种新的递归神经网络，在稳定性和网络训练复杂程度方面都优于传统神经网络，已经成为时间序列预测领域的研究热点。在EWT-ESN的基础上，提出一种基于EWT与ESN相结合的组合预测方法。技术实现要素：本发明提供了一种基于EWT-ESN的短期风电功率预测方法，克服了上述现有技术之不足，其能有效解决现有的风电输出功率预测方法中存在预测精度低且在风电功率变化剧烈的预测点易产生误差的问题。本发明的技术方案是通过以下措施来实现的：基于EWT-ESN的短期风电功率预测方法包括以下步骤：第一步，将具有强非线性和非平稳性的原始风电功率采用EWT算法进行分解，得到N个模态分量，其中F0表示经验尺度分量，F1至FN表示经验小波分量；EWT的计算是将原信号f(t)分解成为N+1个固有模态函数fk(t)，一个fk(t)定义为一组调幅-调频信号，即AM-FM信号：第二步，结合各分解分量F0至FN的特点按照时间序列建立各分量的ESN预测模型，公式如下：其中，η表示预测样本点的个数，xt为由历史风电功率值(yt-1,yt-2,...,yt-Δ)构成的多维输入向量，Δ为嵌入维数，f(·)用ESN预测模型的方法进行构建；第三步，叠加各分量预测结果即得到最终的预测结果；第四步，对预测结果进行误差分析，确定预测评价指标为平均绝对值百分比误差、均方根误差、最大绝对值误差，即：平均绝对值百分比误差公式为：均方根误差公式为：最大绝对值误差为：根据误差评价指标平均绝对值百分比误差、均方根误差、最大绝对值误差进行预测结果误差分析，其中，yi表示实际功率值，表示功率预测值，η表示预测样本点数。下面是对上述发明技术方案的进一步优化或/和改进：上述在第一步中，EWT的算法实现包括以下步骤：Step1:根据原始信号的频谱特性对傅里叶轴进行自适应的分割，分割为N个连续的部分，确定各个分割片段Λn；Step2:在每一个Λn上根据Meyer小波确定经验尺度函数和经验小波函数分别如公式(6)和公式(7)所示：确定好Λn后，经验小波被定义为在每一个Λn上的带通滤波器，再次根据Meyer小波确定经验尺度函数和经验小波函数，公式中ωn与γ之间存在一定的比例关系，即：τn＝γωn，且0<γ<1，公式(6)和公式(7)简化为公式(8)和公式(9)所示：在经验小波变换中，通过选择合适的γ，得到一个紧框架：即则集合是一个紧框架Step3:根据经验尺度函数和经验小波函数确定细节系数和近似系数在构建好一组紧框架的经验小波后，采用传统的小波变换方法定义经验小波变换用F[·]和F-1[·]分别表示傅里叶变换和逆变换，则细节系数由经验小波函数与信号内积产生：近似系数通过经验尺度函数与信号内积产生，公式如下：上式中，和φ1(ω)分别为经验小波函数和经验尺度函数φ1(t)的傅里叶变换形式；Step4:计算得到和通过卷积计算即可得经验尺度分量和经验小波分量，公式如下：原始信号f(t)被重构为：其中，*为卷积符号，和分别为和的傅里叶变换形式；因此，经验模态的定义如下：其中f0(t)由近似系数和经验尺度函数φ1(t)的卷积构成，代表原始信号的整体变化趋势部分，可看作经验尺度分量，fk(t)由细节系数和经验小波函数ψk(t)的卷积构成，可近似地看作表征原序列中不同频域的经验小波分量。上述在第二步中，结合各分解分量F0至FN的特点按照时间序列建立各分量的ESN预测模型，首先给定导师训练样本：即(u(1)，yd(1))，(u(2)，yd(2))，…(u(T)，yd(T))，其中u表示输入序列，y为相应的导师期望输出序列，T为序列最大长度；通过输入输出样本驱动ESN网络，使得网络训练输出y(n)逼近实际期望输出yd(n)，建立ESN预测模型具体包括以下步骤：(1)选择网络结构，即确定输入层、SR层、输出层的维数K、N及L；设ESN网络输入层、SR层及输出层变量的维数分别为K、N及L，网络在n时刻的输入层、SR层及输出层神经元为：(2)初始化网络，输入权值Win、输出反馈权值Wfb分别由[-0.2,0.2]、[-1,1]的均匀分布预先随机设定，内部状态矩阵W以[-1,1]的均匀分布随机生成连接度为min(10/N,1)的稀疏矩阵，并使其谱半径ρ小于1；设网络的输入连接权值矩阵、SR内部连接权值矩阵、输出连接权值矩阵及由输出反馈至SR的反馈连接权值矩阵分别表示为：W＝(wij)，各权值的维数依次为：N×K维，N×N维，L×(K+N+L)维，N×L维；(3)由导师输入向量u(n)和输出向量yd(n)驱动网络运行，更新SR内部状态，则n+1时刻ESN网络SR中内部神经元状态方程为：x(n+1)＝f(Winu(n+1)+ρWx(n)+Wfby(n)+v(n+1))(21)其中，f＝[f1,f2,…,fN]T为内部神经元的激发函数，取双曲正切tanh函数；ρ表示W的谱半径，是具有正态分布或均匀分布的噪声向量；(4)定义矩阵M和D，网络训练中，为消除网络起始瞬态的影响丢弃前T0个值，在时刻T0后，收集网络不同时刻的输入、状态和输出向量，合并(u(n),x(n),yd(n-1))到矩阵M，其维数为(T-T0+1)×(K+N+L)；同时，将不同时刻的期望输出yd(n)的反双曲正切函数tanh-1yd(n)作为矩阵D的行向量，其维数为(T-T0+1)×L；两矩阵M和D的构造分别为：D＝[tanh-1yd(T0+1),tanh-1yd(T0+2),...tanh-1yd(T)]T神经网络输出权值Wout为(Wout)T＝M-1D(22)将式(22)中的(Wout)T转置即为Wout；(5)通过公式(2)、公式(22)计算得ESN的网络输出用输出状态方程表示为：其中，fout取双曲正切tanh函数，矩阵符号[·]表示ESN的输入层、SR层以及输出层向量的合并。本发明首先利用EWT算法将非平稳的风电功率原始序列分解为具有紧支撑傅立叶频谱特性的AM-FM分量，然后利用ESN对各AM-FM分量分别进行预测，并进行叠加以得到最终的预测结果。将EWT-ESN组合预测方法用于不同地区的风电功率实例中，并与EMD-ESN的组合预测方法进行比较，有效验证了本发明方法的有效性。本发明能够有效的提高风电功率预测的精度并降低了风电功率变化剧烈的预测点的误差。附图说明附图1为本发明实施例1的傅里叶轴的分割示意图。附图2为本发明实施例1的滤波器组的周期性示意图。附图3为本发明实施例1的ESN的基本结构示意图。附图4为本发明实施例1的EWT-ESN组合预测方法流程图。附图5为本发明实施例2的EMD分解结果示意图。附图6为本发明实施例2的EWT分解结果示意图。附图7为本发明实施例2的基于EWT-ESN方法的风电功率预测结果示意图。附图8为本发明实施例2的各种方法的风电功率预测结果对比图。附图9为本发明实施例3的EMD分解结果示意图。附图10为本发明实施例3的EWT分解结果示意图。附图11为本发明实施例3的基于EWT-ESN方法的风电功率预测结果示意图。附图12为本发明实施例3的各种方法的风电功率预测结果对比图。具体实施方式本发明不受下述实施例的限制，可根据本发明的技术方案与实际情况来确定具体的实施方公式。下面结合实施例及附图对本发明作进一步描述：实施例1：如附图1、2、3、4所示，基于EWT-ESN的短期风电功率预测方法，包括以下步骤：第一步，将具有强非线性和非平稳性的原始风电功率采用EWT算法进行分解，得到N个模态分量，其中F0表示经验尺度分量，F1至FN表示经验小波分量；即所述EWT的计算将原信号f(t)分解成为N+1个固有模态函数fk(t)，一个fk(t)定义为一组调幅及调频信号，即AM-FM信号，表示公式如下：第二步，结合各分解分量F0至FN的特点按照时间序列建立各分量的ESN预测模型，公式如下：其中，η表示预测样本点的个数，xt为由历史风电功率值(yt-1,yt-2,...,yt-Δ)构成的多维输入向量，Δ为嵌入维数，f(·)用ESN预测模型的方法进行构建；第三步，叠加各分量预测结果即得到最终的预测结果；第四步，对预测结果进行误差分析，确定预测评价指标为平均绝对值百分比误差、均方根误差、最大绝对值误差，即：平均绝对值百分比误差公式为：均方根误差公式为：最大绝对值误差为：根据误差评价指标平均绝对值百分比误差、均方根误差、最大绝对值误差进行预测结果误差分析，其中，yi表示实际功率值，表示功率预测值，η表示预测样本点数。本发明能够有效的提高风电功率预测的精度并通过误差分析有效降低了风电功率变化剧烈的预测点的误差。可根据实际需要，对上述基于EWT-ESN的短期风电功率预测方法作进一步优化或/和改进：如附图1、2、3、4所示，在第一步中，EWT的算法实现包括以下步骤：Step1:根据原始信号的频谱特性对傅里叶轴进行自适应的分割，分割为N个连续的部分，确定各个分割片段Λn；这里的EWT的计算过程依据如下：首先假设将傅里叶支撑区间[0,π]分割成N个连续的部分，ωn表示各个分割片段之间的界限(ω0＝0,ωN＝π)，如附图1所示，各个分割片段可以表示为Λn＝[ωn-1,ωn]，那么以ωn为中心，可以定义一个宽度Tn＝2τn的过度区域，如附图1中的阴影区域所示；Step2:在每一个Λn上根据Meyer小波确定经验尺度函数和经验小波函数分别如公式(6)和公式(7)所示：确定好Λn后，经验小波被定义为在每一个Λn上的带通滤波器，再次根据Meyer小波确定经验尺度函数和经验小波函数，公式中ωn与γ之间存在一定的比例关系，即：τn＝γωn，且0<γ<1，公式(6)和公式(7)简化为公式(8)和公式(9)所示：在经验小波变换中，通过选择合适的γ，得到一个紧框架：即当则集合是一个紧框架Step3:根据经验尺度函数和经验小波函数确定细节系数和近似系数如公式(10)和公式(11)所示，在构建好一组紧框架的经验小波后，采用传统的小波变换方法定义经验小波变换，用F[·]和F-1[·]分别表示傅里叶变换和逆变换，则细节系数由经验小波函数与信号内积产生：近似系数通过经验尺度函数与信号内积产生，公式如下：上式中，和φ1(ω)分别为经验小波函数和经验尺度函数φ1(t)的傅里叶变换形式；Step4:计算得到和通过卷积计算即可得经验尺度分量和经验小波分量，具体计算过程如下：原始信号f(t)被重构为：其中，*为卷积符号，和分别为和的傅里叶变换形式；因此，经验模态的定义如下：其中f0(t)由近似系数和经验尺度函数φ1(t)的卷积构成，代表原始信号的整体变化趋势部分，可看作经验尺度分量，fk(t)由细节系数和经验小波函数ψk(t)的卷积构成，可近似地看作表征原序列中不同频域的经验小波分量。在上述Step2中，这里沿用Meyer小波构造的思想，即如果则集合是一个紧框架附图2为周期为为2π的滤波器组，则有：其中，Λσ(n)与Λn一样，只是Λn以νn为中心，而Λσ(n)以2π-νn为中心。首先，可以看出，对于可以得到：那么，需要进一步来观察过渡区域，根据β所具有的特性，则这个结果同时也适用于连续无重叠的Tn：τn+τn+1<ωn+1-ωn(18)只有公式(20)满足最小的Tn，才能保证得到紧框架，因此，如果则集合是一个紧框架如附图1、2、3、4所示，在第二步中，结合各分解分量F0至FN的特点按照时间序列建立各分量的ESN预测模型，首先给定导师训练样本：即(u(1)，yd(1))，(u(2)，yd(2))，…(u(T)，yd(T))，其中u表示输入序列，y为相应的导师期望输出序列，T为序列最大长度；通过输入输出样本驱动ESN网络，使得网络训练输出y(n)逼近实际期望输出yd(n)，建立ESN预测模型具体包括以下步骤：(1)选择网络结构，即确定输入层、SR层、输出层的维数K、N及L；设ESN网络输入层、SR层及输出层变量的维数分别为K、N及L，网络在n时刻的输入层、SR层及输出层神经元为：(2)初始化网络，输入权值Win、输出反馈权值Wfb分别由[-0.2,0.2]、[-1,1]的均匀分布预先随机设定，内部状态矩阵W以[-1,1]的均匀分布随机生成连接度为min(10/N,1)的稀疏矩阵，并使其谱半径ρ小于1；设网络的输入连接权值矩阵、SR内部连接权值矩阵、输出连接权值矩阵及由输出反馈至SR的反馈连接权值矩阵分别表示为：W＝(wij)，各权值的维数依次为：N×K维，N×N维，L×(K+N+L)维，N×L维；(3)由导师输入向量u(n)和输出向量yd(n)驱动网络运行，更新SR内部状态，则n+1时刻ESN网络SR中内部神经元状态方程为：x(n+1)＝f(Winu(n+1)+ρWx(n)+Wfby(n)+v(n+1))(21)其中，f＝[f1,f2,…,fN]T为内部神经元的激发函数，取双曲正切tanh函数；ρ表示W的谱半径，是具有正态分布或均匀分布的噪声向量；(4)定义矩阵M和D，网络训练中，为消除网络起始瞬态的影响丢弃前T0个值，在时刻T0后，收集网络不同时刻的输入、状态和输出向量，合并(u(n),x(n),yd(n-1))到矩阵M，其维数为(T-T0+1)×(K+N+L)；同时，将不同时刻的期望输出yd(n)的反双曲正切函数tanh-1yd(n)作为矩阵D的行向量，其维数为(T-T0+1)×L；两矩阵M和D的构造分别为：D＝[tanh-1yd(T0+1),tanh-1yd(T0+2),...tanh-1yd(T)]T神经网络输出权值Wout为(Wout)T＝M-1D(22)将式(22)中的(Wout)T转置即为Wout；(5)通过公式(2)、公式(22)计算得ESN的网络输出用输出状态方程表示为：其中，fout取双曲正切tanh函数，矩阵符号[·]表示ESN的输入层、SR层以及输出层向量的合并。可以证明，ESN状态池SR的连接权矩阵的谱半径小于1时，该网络是渐进稳定的。这里的ESN预测模型的核心结构由随机生成且稀疏连接的SR构成，能够起到存储历史信息的“回声”作用，SR的参数随机产生且在整个学习过程中固定不变，只需调整输出权值，因而ESN具有学习算法简单高效的优点，克服了RNN网络在大规模网络训练应用中要求时序偏微分等计算导致的计算复杂，训练困难等缺点。如附图3所示，ESN的基本网络结构从图中可看出网络分为输入层、SR层、输出层三层。输入层以及SR层与输出层之间的虚线连接为输出权值，实线部分的连接权值在网络训练前一经产生就不再改变，仅虚线连接部分的权值在网络训练中需要学习，即ESN只需计算网络输出权值即可完成整个训练过程，其学习算法简单高效。黑色线条代表的连接是网络中必须存在的，而灰色线条代表的连接是可以选择的。ESN网络的SR是由大量随机生成且稀疏连接的神经元组成，蕴含了系统的运行状态，并具有记忆功能，形成一个巨大的动态记忆库。网络初始化时，SR中神经元之间的连接权值随机产生，并保持1％-5％的连接密度(S)。在SR构建完成后，输入神经元再与SR中的所有神经元相连。实施例2：如附图5、6、7、8和表1、表2所示，根据加拿大阿尔伯塔省风电场2010年12月1日到27日之间的实测风电功率数据，原始数据集的采样间隔为10min，本发明中以30min为采样间隔来获取实验数据集，取前80％的数据作为训练样本，其余20％的数据作为测试样本。对原始数据集分别采用EMD和EWT方法进行分解，分解结果分别如附图5和附图6所示，可以看出，EWT和EMD的分解结果存在很大的差异，首先EWT分解得到6个模态分量，而EMD分解得到8个模态分量，因此EWT有效的降低了构建预测模型的个数，节省了组合预测的计算规模；其次，EMD的分解得到的IMF分量表现出从高频到低频变化的规律，其高频分量IMF1和IMF2幅值波动剧烈(无论怎样建立预测模型均难以取得准确的预测)，两者共占原始分量X幅值比例的30％左右，因此IMF1和IMF2的预测误差会给最终的预测结果带来一定的累计误差。EWT的分解分量则呈现出从低频到高频变化的特点，其低频分量F0和F1的波动较为规律(可以得到很高的预测精度)，且两者幅值较大，大约占原始分量X幅值的90％左右，分量F3-F5虽然波动较为剧烈，但其幅值相对原始信号很小，不会给最终的预测结果带来太大的影响，仅有分量F2会产生一定的预测误差。对分量F0至F5分别构建不同的ESN预测模型进行预测，各分预测模型中，分量F2和F4嵌入维数Δ＝2，其余分量嵌入维数均为3，叠加各分量预测结果即得到最终的预测结果。附图7给出了EWT-ESN方法的测试样本的前50个样本点(共259个样本点)的预测效果图，由附图7可知，除个别突变剧烈的点有较小的误差外，本发明能够实现对风电功率进行有效的预测。在各ESN预测模型中，储备池(SR)的大小、谱半径ρ和网络连接稀疏度S主要参数通过交叉验证的方法选取，以得到较优的实验结果。具体参数的取值如表1所示。本实施例的预测方法与EMD结合ESN的组合预测方法以及ESN单一预测方法做了比较，为更加清晰的观察本发明方法的预测效果，截取了各种预测方法的前50个样本点的预测效果予以对比，从附图8可看出，EWT-ESN方法的预测效果最优。同时，表2还列出了各种预测方法的预测误差指标，本发明方法的预测精度从三个预测指标上优于EMD结合ESN的组合预测方法所获得的结果。实施例3：如附图9、10、11、12和表3、表4所示，根据新疆乌鲁木齐地区中节能风电一场的9月23日到9月30日的实测风电功率数据，数据集的采样间隔为15min。取前7天的数据作为训练数据集，30日的数据集(96的样本点)作为测试数据集来验证本发明的预测效果。根据附图9和附图10所示，采用EMD和EWT方法对8天的原始数据进行分解得到的分解结果图，同实施例2，EWT和EMD的分解结果存在很大的差异，EWT分解得到了5个模态分量，而EMD分解得到了8个模态分量；其次，EWT分解到到的分量F0的幅值占原始原始分量x的比例很大，且其变化很平稳，其余分量幅值都很小，这为最终取得较优的预测结果提供了基础。同实施例2，对分量F0至F4分别构建不同的ESN预测模型进行预测，各分预测模型中，分量F0至F2嵌入维选为3，F3和F4嵌入维为4，叠加各分量预测结果即得到最终的预测结果。各ESN预测模型的具体参数取值如表3所示。如附图11所示，根据EWT-ESN方法测试样本的后50个样本点(共96个样本点)预测效果图可看出,本发明取得了比实施例2更好的预测效果。各种预测方法的预测效果对比图如附图12所示。表4给出了各种预测方法的预测误差指标，从表4可以看出，EMD-ESN方法在本实施例中并没有取得较理想的预测结果，结合附图10，EMD-ESN方法在每个预测点都产生了一定的误差，相对于单一预测方法，其MAPE指标并没有提高很多，而本发明方法的三个预测指标上都取得了很高的预测精度。以上技术特征构成了本发明的实施例，其具有较强的适应性和实施效果，可根据实际需要增减非必要的技术特征，来满足不同情况的需求。表1ESN模型的参数取值ESN参数SRρSF0300.800.011F1250.900.020F2200.950.050F3300.800.020F4200.900.020F5300.900.020表2EWT-ESN与其他预测方法的性能比较预测方法MAPERMSEMEESN8.461838.5697160.9639EMD-ESN4.171417.964881.4545EWT-ESN3.473415.165554.6868表3ESN模型的参数取值ESN参数SRρSF0300.900.011F1200.800.020F2300.850.030F3300.800.030F4350.900.050表4EWT-ESN与其他预测方法的性能比较预测方法MAPERMSEMEESN9.56403.757614.6498EMD-ESN8.34362.11309.4934EWT-ESN2.09740.42031.5774当前第1页1 2 3