基于环境特征和随机方法的柔性针路径规划方法与流程

本发明涉及医学技术领域，尤其涉及一种基于环境特征和随机方法的柔性针路径规划方法。

背景技术：

微创介入治疗是在影像导引下，以最小的创伤将器具或药物投送到目标病灶，对其进行诊断和治疗的技术，它对临床医学的发展起到关键作用。而穿刺作为一种最为常用的介入技术，多被用于药物置入、病理诊断、放射治疗等手术中。传统手术采用刚性针的直线运动来实现穿刺，直线进针时路径受限，且由于刚性针的自然形变引起靶点定位误差，严重影响治疗效果。相比而言，柔性针穿刺利用针体的形变在软组织内实现曲线运动，能灵活的避开骨骼和血管等障碍物，准确的到达目标点(如图1)。

单轮车模型作为柔性针的运动学模型被Webster等人提出，从此柔性针软组织穿刺成为国内外研究的热点。路径规划对柔性针穿刺的研究有重要意义。Park等人通过建立概率密度函数对柔性针路径进行规划，但此算法只适用于无障碍环境。Alterovitz等人建立非线性目标函数规划柔性针的穿刺路径，但此方法只适用于定曲率的圆弧路径。Xu等人利用运动学反解法规划柔性针路径，该算法在有障碍物的情况下必须给出过渡点的位姿，这不能保证有解。Patil等人基于快速搜索随机树(RRT)算法规划柔性针的穿刺路径，虽然提高了规划速度，但它规划的是可行路径，并非最优路径。

由上述研究可看出，柔性针软组织穿刺的路径规划算法还有待改善，在基于柔性针穿刺环境的方面的研究很少。目前快速搜索随机树(RRT)算法在路径规划中得到了广泛的应用，它的优点是算法的流程简单、搜索速度快，且能在有障碍的环境中避开障碍准确到达目标点。最初的RRT算法是由S.M.LaValle等人提出的，为了提高该算法的效率和性能，RRT的改进方法被不断的提出。作者前期在柔性针路径规划上，提出了考虑柔性针运动学模型，基于路径最短、最安全及弧段数最少的路径评估函数的改进的快速搜索随机树(I-RRT)算法规划路径。

虽然，I-RRT算法通过基于路径长度、安全度及弧段数的路径评估函数规划路径，在一定程度上优化了柔性针的穿刺路径，但算法对穿刺环境的适应性不强。在实际情况中，在路径规划前，医生难以结合临床经验对规划的路径进行修正。

技术实现要素：

本发明的目的在于解决上述现有技术存在的缺陷，提供一种基于环境特征和随机方法对柔性针软组织穿刺的路径进行规划的方法，使医生能在术前结合临床经验选择更为合理的路径。

一种基于环境特征和随机方法的柔性针路径规划方法，包括根据评估函数Evaluation_Function()选择最优的规划路径；

其中，路径评估函数Evaluation_Function()的表达式为：

F＝w₁F_L+w₂F_S+w₃F_N (1)

其中，F_L是路径长度评估函数，F_L＝L/L_avg，L是路径的长度，L_avg是生成的所有样本路径的长度L的平均值；F_S是安全评估函数，F_S＝S/S_avg，S是障碍物距每段弧的距离小于一个预设长度D₁的数目，S_avg是规划的样本路径的5的平均值；F_N是弧段数评估函数，F_N＝N/N_avg，N是路径的弧段数，N_avg是规划的样本路径的N的平均值，w₁，w₂和w₃表示各子函数对应的权重系数；所述权重系数根据医生的临床经验进行设定。

进一步地，如上所述的方法，所述权重系数根据医生的临床经验进行设定包括：医生根据自身的临床经验判断F_L、F_N、F_S这三个评估函数在实际情况中哪个更为重要，根据重要程度将对应的权重系数调高，将相对不重要的评估函数对应的权重系数调低。

一种基于环境特征和随机方法的柔性针路径规划方法，包括根据考虑障碍物风险分级的路径评估函数ObsGrade_Function()选择最优的规划路径；

其中，ObsGrade_Function()的表达式为：

F′＝w₁F_L+w₂f/f_avg+w₃F_N (2)

其中，F_L是路径长度评估函数，F_L＝L/L_avg，L是路径的长度，L_avg是生成的所有样本路径的长度L的平均值；F_N是弧段数评估函数，F_N＝N/N_avg，N是路径的弧段数，N_avg是规划的样本路径的N的平均值，f是风险分级评估函数，f_avg是规划的样本路径的f的平均值，f表达式为：

其中，i(i＝1，2...n)表示各障碍物的风险等级，G_i表示相对应的风险等级障碍物距每段弧的距离小于一个预设长度D₂的数目；a_i表示对应的风险等级系数，风险级别越高，相对应的a_i值越大；

w₁，w₂和w₃表示各子函数对应的权重系数；所述权重系数根据医生的临床经验进行设定。

进一步，如上所述的方法，所述权重系数根据医生的临床经验进行设定包括：医生根据自身的临床经验判断F_L、F_N、f这三个评估函数在实际情况中哪个更为重要，根据重要程度将对应的权重系数调高，将相对不重要的评估函数对应的权重系数调低。

进一步，如上所述的方法，所述路径的计算方法包括以下步骤：

步骤1：建立一棵树T，起始点x_init为其根节点；

步骤2：在无障碍物空间X_free中随机选取某个状态点x_rand；

步骤3：基于点x_rand执行Extend()对树进行扩展，得到一个新的节点x_new；

步骤4：将此新节点添加到树中，重复以上步骤，直到找到目标点为止；

步骤5：重复步骤1-4，规划出多条样本路径；

其中，Extend()的具体步骤为：

(1)在树上找到离x_rand最近的点x_near；

(2)选择一个控制输入量U，将其作用在x_rand得到新的点x_new；

(3)根据x_rand、x_near、x_new这三个参数确定一段新的圆弧，即Arc_new；

(4)检测弧Arc_new看其是否在无障碍空间X_free中，并且检测弧Arc_new的半径r_new是否大于r_min；

(5)判断搜索是否成功，如果||x_new-x_goal||＜ε，ε是一个事先设定好的非常小的常数，表示搜索成功，算法停止。

本发明技术方案带来的有益效果：

本发明基于环境特征和随机方法规划的路径对环境的适应性好，路径规划前，医生可以依靠自己都经验，根据环境特性及计划任务要求等来手动设置权重系数，权重系数的调整给算法和用户提供了一个交互式的设计方法；另外，本发明在路径规划时，可以提前设置障碍物的风险等级，再通过考虑障碍物风险分级的路径评估函数，选出远离高风险障碍物、路径短且弧段数少的穿刺路径。

附图说明

图1为柔性针软组织穿刺示意图；

图2为I-RRT算法示意图；

图3为基于I-RRT算法规划的40条样本路径；

图4为通过路径评估函数在样本路径中选出的最优路径；

图5在障碍物多而小的环境中选择的最优路径；

图6在障碍物少而大的环境中选择的路径；

图7障碍物风险分级环境图；

图8障碍物风险分级规划的路径。

具体实施方式

为使本发明的目的、技术方案和优点更加清楚，下面本发明中的技术方案进行清楚、完整地描述，显然，所描述的实施例是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有作出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。

如图2所示，I-RRT算法的基本思想：1.建立一棵树T，起始点x_init为其根节点；2.在无障碍物空间X_free中随机选取某个状态点x_rand；3.基于点x_rand执行Extend()对树进行扩展，得到一个新的节点x_new；4.将此新节点添加到树中，重复以上步骤，直到找到目标点为止。5.重复步骤1-4，规划出多条样本路径，通过路径评估函数Evaluation_Function()选出最优路径。其中，Extend()的具体步骤：(1)在树上找到离x_rand最近的点x_near；(2)选择一个控制输入量U，将其作用在x_rand得到新的点x_new；(3)通过Generate_arc()函数，计算得到新的弧Arc_new；(4)在Collision()函数中检测弧Arc_new看其是否在无障碍空间X_free中，并且检测弧Arc_new的半径r_new是否大于r_min；(5)判断搜索是否成功，如果||x_new-x_goal||＜ε(ε是一个事先设定好的非常小的常数)，表示搜索成功，算法停止。

从以上可以看出，虽然，I-RRT算法通过基于路径长度、安全度及弧段数的路径评估函数规划路径，在一定程度上优化了柔性针的穿刺路径，但算法对穿刺环境的适应性不强。在实际情况中，在路径规划前，医生难以结合临床经验对规划的路径进行修正。

而本发明基于环境特征和随机方法在规划柔性针软组织穿刺路径上相较于I-RRT算法的区别主要有两点：1.路径评估函数的权重系数的调整。医生根据环境中障碍物的多少、大小不同来手动设置路径评估函数中的权重系数，再通过评估函数选择相对应的最优路径；2.障碍物风险分级。医生结合自身经验提前判断每个障碍物的风险级别，再通过考虑障碍物风险分级的路径评估函数，选择尽可能远离风险级别高的障碍物、路径短且弧段数少的路径。

首先，创建三个穿刺环境，分别为：第一个穿刺环境为柔性针穿刺的初始环境；第二个穿刺环境为障碍物数目多而半径小的环境；第三个穿刺环境为障碍物数目少而半径大的环境。其次，在不同的穿刺环境下，基于考虑柔性针的运动特征的RRT算法，在3个穿刺环境中都规划出多条样本路径，根据穿刺环境调整路径评估函数Evaluation_Function(l，saft，n)的权重系数，选择在不同穿刺环境下所对应的最优路径。最后，对初始环境中的障碍物设置不同的风险等级，基于考虑柔性针的运动特征的RRT算法规划出多条样本路径，再通过考虑障碍物风险分级的路径评估函数ObsGrade_Function(l，n，grade_obs)选出的最优路径。

其中，基于考虑柔性针的运动特征的RRT算法的流程为：1.建立一棵树T，起始点x_init设为其根节点；在无障碍物空间X_free中随机选取某个状态点x_rand；基于点x_rand执行Extend()对树进行扩展，得到一个新的节点x_new；将此新节点添加到树中，重复以上步骤，直到找到目标点为止；5.重复步骤1-4，规划出多条样本路径。Extend()的具体步骤：(1)在树上找到离x_rand最近的点x_near；(2)选择一个控制输入量U，将其作用在x_rand得到新的点x_new；(3)根据x_rand、x_near、x_new这三个参数确定一段新的圆弧，计算得到新的弧Arc_new；(4)检测弧Arc_new看其是否在无障碍空间X_free中，并且检测弧Arc_new的半径r_new是否大于r_min：(5)判断搜索是否成功，如果||x_new-x_goal||＜ε(ε是一个事先设定好的非常小的常数)，表示搜索成功，算法停止。

在实际柔性针穿刺过程中，第一，规划的路径长度总是希望越短越好；第二，如果柔性针距离血管等障碍物太近时，可能会对患者产生较大的创伤，因此，应尽量远离障碍物；第三，为了使得控制简单且准确，圆弧的段数越少越好。因此，基于以上几个因素的路径评估函数Evaluation_Function()的表达式为：

F＝w₁F_L+w₂F_S+w₃F_N (1)

路径评估函数F包含3个评估子函数：F_L是路径长度评估函数，F_L＝L/L_avg(L是路径的长度，L_avg是生成的所有样本路径的长度L的平均值)；F_S是安全评估函数，F_S＝S/S_avg(S是障碍物距每段弧的距离小于一个预设长度D₁的数目，S_avg是规划的样本路径的S的平均值)；F_N是弧段数评估函数，F_N＝N/N_avg(N是路径的弧段数，N_avg是规划的样本路径的N的平均值)。w₁，w₂和w₃表示各子函数对应的权重系数，所述权重系数根据医生的临床经验进行设定。在障碍物多少、大小不同环境中，路径评估函数的权重系数可以根据医生的经验进行调整，以反映路径选择的优先权。最后，将评估函数值F最小的路径作为规划结果。

所述权重系数根据医生的临床经验进行设定包括：医生根据自身的临床经验判断F_L、F_N、F_S这三个评估函数在实际情况中哪个更为重要，根据重要程度将对应的权重系数调高，将相对不重要的评估函数对应的权重系数调低。

在实际的穿刺环境中，人体中重要的血管和神经等对外物的敏感度高，当柔性针距离人体重要血管和神经等太近时对患者的损伤风险很大。因此，柔性针的路径首先需要尽可能的远离神经等风险级别高的障碍物。医生先判断障碍物的风险等级，预先将障碍物风险分成n级。然后，再通过考虑障碍物风险分级的路径评估函数0bsGrade_Function()选出距离高风险障碍物远、路径短且弧段数少的路径。因此，考虑障碍物风险分级的路径评估函数ObsGrade_Function()的表达式为：

F′＝w₁F_L+w₂f/f_avg+w₃F_N (2)

式中，F_L及F_N与式(2)中的F_L、F_N相同。f是风险分级评估函数，表达式为：

其中，i(i＝1，2...n)表示各障碍物的风险等级，G_i表示相对应的风险等级障碍物距每段弧的距离小于一个预设长度D₂的数目；a_i表示对应的风险等级系数，风险级别越高，相对应的a_i值越大。f_avg是规划的样本路径的f的平均值。最后，将F′值最小的作为规划的路径。

仿真结果和分析

通过MATLAB编写柔性针软组织穿刺的路径规划算法。仿真设计和结果描述如下。

基于I-RRT算法规划的路径

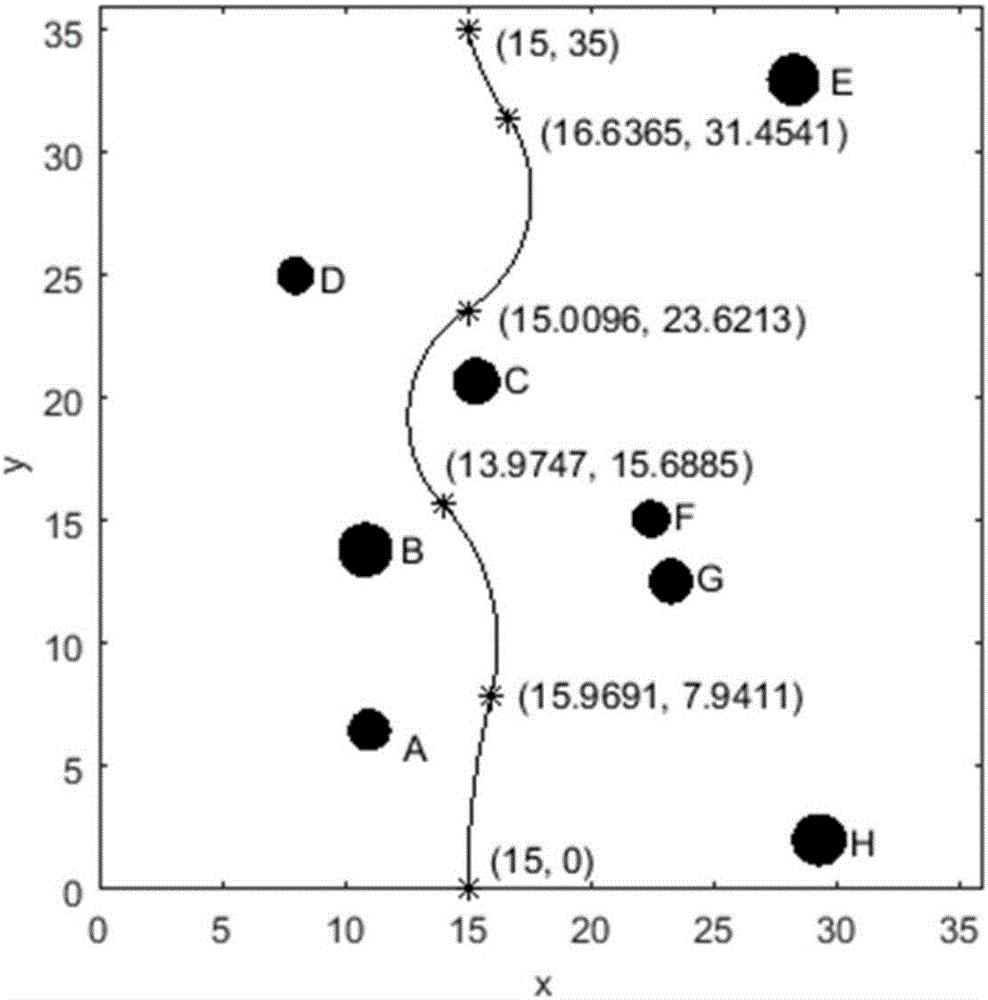
在初始的环境中，有8个大小不等的障碍物A、B、C、D、E、F、G、H，环境的区间为高36，宽36。在仿真中，定义穿刺点x_init为(15,0)，目标点x_goal为(15,35)，进针方向垂直于x轴，针面面向y轴。如图3所示，基于I-RRT算法，规划了40条样本路径。更多的可行路径也可以通过此算法生成。因此，通过路径评估函数来选择路径是非常重要的。

通过评估函数F＝w₁F_L+w₂F_S+w₃F_N选出最优路径。其中，权重系数设置为：w₁＝2，w₂＝1，w₃＝2，F_L、F_S、F_N和F在每个样本路径中被计算。如图4所示，在这40个样本路径中选出F值最小的路径作为最优路径。

基于I-RRT算法规划的柔性针软组织穿刺路径，综合考虑路径长度、安全性和弧段数这几个因素，在一定程度上优化了路径。但算法的环境适应性不强，在实际情况中，在路径规划前，医生很难根据穿刺的环境性质结合自身的经验选择更为合理的路径。

基于环境特征和随机方法规划的路径

权重系数的设置

环境特征包含环境内障碍物数目及半径的大小。在不同的环境中，路径评估函数的权重系数可以根据人的经验进行调整，以适应相应的环境。在仿真中，路径规划首先被完成在初始的环境中，此时权重系数被设置为w₁＝2，w₂＝1，w₃＝2，优选路径如图4所示。

另一个路径规划完成在障碍物数量多但半径小的环境中，在这种情况下，应以路径的长度为重，同时也与安全度和弧段数有关。因此，权重系数被设置为w₁＝5，w₂＝1，w₃＝1，选择的路径如图5所示。

此外，还有一个路径规划完成在障碍物数量少但半径大的环境中，在这种情况下，应以安全度为重，同时也与长度和弧段数有关。因此，权重系数被设置为w₁＝1，w₂＝5，w₃＝1，选择的路径如图6所示。

表1环境不同时选择的路径的评估函数值

不同的环境下选择的各路径的子函数值如表1所示。由图4-6及表1可知，相对于图5(初始环境)中规划的路径，图5对应的路径长度评估函数值F_L＝0.8738小于初始环境中的长度评估函数值F_L＝0.9353，因此图5中的路径在路径长度上具有更好的性能；而图6对应的安全评估函数值F_S＝0.3846小于初始环境中的安全评估函数值F_S＝0.5405，因此图6中的路径在安全度上具有更好的性能。

在实际情况中，在路径规划前能根据环境特性及计划任务要求等来手动设置权重系数。因此，权重系数的调整给算法提供了一个交互式的思想。医生的经验和环境数据统计可以帮助确定权重系数。

障碍物风险分级

环境特征还包含障碍物的风险等级，提前设置障碍物的风险等级，再通过考虑障碍物风险分级的路径评估函数，选出远离高风险障碍物、路径短且弧段数少的穿刺路径。先对障碍物进行风险分级，将障碍物分为2级。如图7所示，环境内有障碍物A、B、C、D、E、F、G、H，其中，黑色圆形的障碍物(A、D、E、F、G、H)代表风险级别低的障碍物，风险级别为1；黑色三角形的障碍物(B、C)代表风险级别高的障碍物，风险级别为2。因此，考虑障碍物风险分级的路径评估函数F′＝w₁F_L+w₂f/f_avg+w₃F_N中的风险分级评估函数可写为f＝a₁G₁+a₂+G₂，仿真中，取a₁＝1，a₂＝5，通过考虑障碍物风险分级的路径评估函数ObsGrade_Function()选出的最优路径如图8所示。

表2障碍物中心离路径的最短距离

将障碍物分级规划的路径与图4中基于I-RRT算法(障碍物未分级)规划的路径相比较，每个障碍物中心离路径的最短距离如表2所示，相对于图4中规划的路径，图8中的路径距离风险级别为2(B和C障碍物)的障碍物更远。因此，在规划路径前，医生可以根据临床经验，判断障碍物的风险等级，帮助选出更为合理的穿刺路径，对障碍物风险的分级提供另一种交互思想。

最后应说明的是：以上实施例仅用以说明本发明的技术方案，而非对其限制；尽管参照前述实施例对本发明进行了详细的说明，本领域的普通技术人员应当理解：其依然可以对前述各实施例所记载的技术方案进行修改，或者对其中部分技术特征进行等同替换；而这些修改或者替换，并不使相应技术方案的本质脱离本发明各实施例技术方案的精神和范围。