一种天然气系统能流计算的改进方法与流程

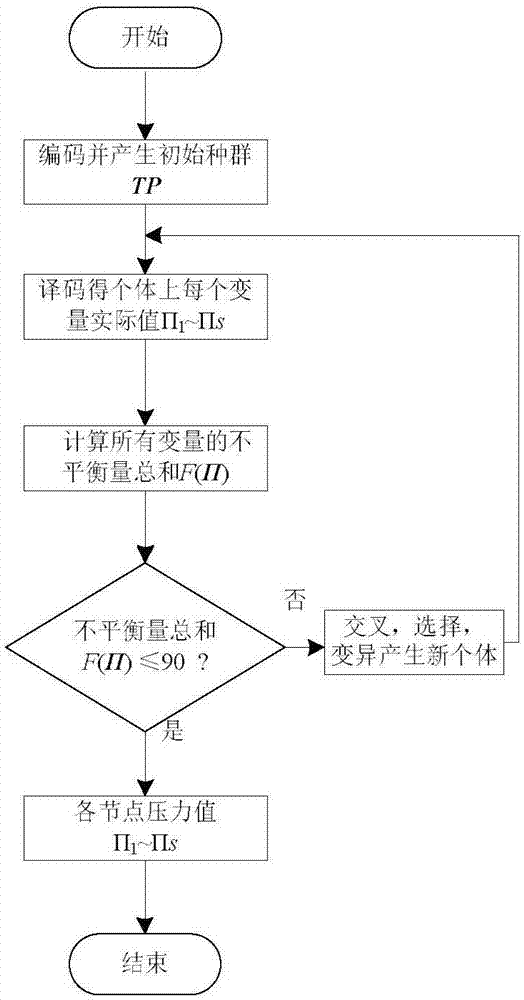
本发明属于天然气系统稳态能流计算
技术领域：
，具体涉及到一种天然气系统稳态能流计算的改进方法。
背景技术：
：能流计算是天然气系统的一种基本计算，是天然气系统规划和运行的基础。现有天然气系统能流计算均以牛顿法为核心算法。牛顿法是一种优秀的局部搜索算法，具有局部二次收敛性。但其对初值的依赖性较高，初值选取不当将直接影响算法的收敛性。关于天然气系统的初值问题，尽管部分研究特别指出需要慎重选取天然气系统的初值，但现有研究并未给出有效的解决办法，而更多地依赖工程经验来确定初值。如2012年27卷第4期《IEEETransactionsonPowerSystems》中“Aunifiedgasandpowerflowanalysisinnaturalgasandelectricitycouplednetworks”和2015年第31卷第5期《IEEETransactionsonPowerSystems》中“AnIntegratedSteady-StateOperationAssessmentofElectrical,NaturalGas,andDistrictHeatingNetworks”均提出以天然气系统平衡节点压力作为参考，按天然气管道首、末两端压力差为5％-10％来选取节点压力的初值，但该方法对复杂网络(即能流计算前无法确定全部气流方向的网络)并不适用。综上可知，现有研究并未给出有效方法解决天然气系统能流计算的初值选取问题。技术实现要素：本发明的目的是针对现有天然气系统能流计算初值难以选取的问题，结合遗传算法的全局搜索和牛顿法的局部搜索能力，提供了一种计算天然气系统能流的遗传-牛顿混合方法。实现本发明之技术方案是：一种天然气系统能流计算的改进方法，首先输入天然气系统的网络参数，建立天然气系统能流计算模型；利用遗传算法进行天然气系统的初值优选；最后，利用牛顿法实现天然气系统的能流计算。所述方法的具体步骤如下：一种天然气系统能流计算的改进方法，其特征在于，包括以下步骤:(1)输入基础数据及初始化1.1输入基础数据获取天然气系统网络结构数据：气源参数、输气管道参数、压缩机参数、气负荷、平衡节点压力以及待求节点压力范围。1.2参数初始化设置遗传算法的交叉概率PC，变异概率Pm，变量精度esp，种群规模Pop，表示种群中全部个体所在集合；牛顿法收敛精度ε，牛顿法的最大迭代次数iterNWmax。设置天然气系统中除平衡节点外的节点个数为N；表示网络N个节点所在的集合。(2)基于遗传算法的初值优选2.1编码并产生初始种群第(1)步完成之后，以一个非平衡节点上的节点压力为一个变量，则一共有N个变量，根据变量范围和变量精度，按照二进制编码方法，确定第s(s＝1,2,···,N)个变量对应的二进制串长度为ns，其数值满足下列关系式：式中esp的值在步骤1.2中给出；Πmax,s、Πmin,s分别表示第s个节点压力变量的上限和下限；确定每个变量对应的二进制串长度后，每个个体包含N个变量的二进制串，则确定每个个体的染色体长度为运用Matlab产生基于状态变量的初始种群TP，种群规模均为Pop。具体步骤为：运用Matlab命令rand(Pop,L)产生一个Pop×L的矩阵T，其元素值为区间(0,1)上的随机数；然后判断矩阵T中的每个元素，若值小于0.5，则该元素置为0，否则置为1；从而得到二进制编码的矩阵TP。其中，TP的每一行表示携带N个节点压力变量信息的一个个体，是位数为L的二进制码。2.2译码并得变量的实际值将各个二进制编码转换为对应的变量的实际值Πm_s，转换公式如下：式中，TPm_s表示第m个个体上第s个节点压力变量的二进制编码，即二进制编码矩阵TP的第m行第至第列二进制编码，Πm_s表示TPm_s代表的变量实际值，(TPm_s)D表示TPm_s对应的变量的十进制数值，求取公式为：其中Al表示TPm_s的第l位二进制数；其余变量的含义同公式(1)-(2)。2.3计算个体对应的目标函数值2.3.1.计算管道流量根据步骤个体中各个节点的压力变量实际值，得管道i-j流量fp,ij的计算公式如下：式中，下标p表示管道，i表示系统中的某一节点i，j表示与节点i直接相连的另一个节点，j∈φi，φi为与节点i直接相联但不包括节点i的节点集合；kij为管道的传输参数，是与管道的长度、内径、摩擦系数以及天然气温度等有关的常数，例如下表：表1节点管道参数kij管道首端节点i管道末端节点jkij120.2526130.2410230.2990240.2924360.2777580.23657100.16629120.163411130.149312130.159812140.166513140.1534Πi和Πj分别表示节点i和节点j的节点压力，已从步骤2.2中获得；sp,ij表示的是节点i，j间管道中的气流方向，其取值如下所示：2.3.2计算燃气轮机消耗的气流量由管道方程可知，天然气在传输过程中会有压力损失，一般需要在天然气系统中配置压缩机来提升压力。选择燃气轮机作为压缩机，选择作用于节点i和节点j间的压缩机，记为压缩机i-j，则其消耗的气流量公式如下：τc,ij＝αc+βcHc,ij+γcHc,ij2(26)式中，下标c代表压缩机编号；αc，βc，γc为能量转化效率常数，其取值由燃气轮机的耗热率曲线决定，例如下表：表2燃气轮机耗热率参数节点i编号节点j编号αcβcγc17070812070Hc,ij为压缩机消耗的功率，其求取公式如下：式中，Bc,ij和Zc,ij均为压缩机参数，其取决于压缩机的温度、效率、压缩因子等因素，例如下表：表3压缩机参数表入口出口BkZk45228.740.2333567226.020.2333589228.740.233351011226.020.23335fc,ij为流过压缩机i-j的气流量，其余变量的含义同公式(5)。2.3.3计算天然气系统的节点能流平衡方程天然气系统中，节点i的能流平衡方程如下所示：式中，fi为节点i的注入气流量，sc,ij是用来表示压缩机的方向的符号变量，其公式如下：式(9)其余变量含义与式(5)到式(8)一样。2.3.4.计算目标函数值将天然气系统中能流方程中各节点不平衡量的总和作为目标函数值。假设对于天然气系统，其能流方程的一般形式为：则代入每个节点的压力实际值至式(9)，得出每个节点对应的注入气流量的不平衡量如下：Δfs(Π)＝fs-fs(Π1,Π2,…,ΠN)(31)算出每个节点的注入其流量的不平衡量Δfs(Π)，得出能流方程中不平衡量的总和为：式中，F(Π)为目标函数，即能流方程中不平衡量的总量。2.4收敛判据计算出每一个个体对应的目标函数Fm(Π)，比较目标函数的大小，选出其中的最小值minF(Π)。遗传算法的收敛条件是，若minF(Π)小于阈值，则满足收敛条件，将minF(Π)对应的个体中的每个变量作为初值，代入步骤(3)；若不满足收敛条件，即继续执行步骤2.5，直至满足收敛条件为止。2.5产生新个体2.5.1选择步骤2.3计算完初始种群TP的全部个体对应的目标函数后，需要用适应度大小评判个体优劣，从而决定其遗传机会的多少。以不平衡量总和F(Π)最小作为优化目标时，个体m的适应度函数如下：式中：fm为表示第m个个体对应的适应度值，Fm(Π)为第m个个体对应的目标函数值。采用轮盘赌选取，每个个体被选中的概率为具体操作为：在区间[0,1]产生一个均匀分布的随机数r，若满足则表示个体w被选中。重复选择Pop次，得到Pop个经过选择后的个体，组成父代种群Tf。2.5.2交叉对父代种群Tf进行交叉操作。具体步骤为：将种群Tf中的个体和作为父代，对父代第1个变量对应的二进制码，运用Matlab命令rand()随机产生一个(0,1)上的数r,若r<Pc(Pc为交叉概率，已在步骤1.2中给出)，n1为第一个变量的二进制串长度，取rn1的整数部分c1作为第1个变量的二进制码交叉点位置，将父代个体和中第1个变量的二进制码的第c1至n1位进行互换，按照同样方法，对父代和中剩下的N-1个变量进行二进制码交叉操作，得到子代个体和从而可以得到新的子代种群Tson，并且该种群规模保持Pop个个体不变。2.5.3变异对子代种群Tson进行变异操作，具体步骤为：对种群Tson中的个体对个体上第1个变量对应的二进制码，运用Matlab命令rand()随机产生一个(0,1)上的数r，若r<Pm(Pm为变异概率，已在步骤1.2中给出)，取rn1的整数部分d1作为第1个变量二进制码的变异点位置，则该个体第1个变量二进制码的第d1位二进制数发生变异，即原来为1则变为0，原来为0则变为1，若r>Pm，则该变量对应的二进制码不变，对该个体上剩下的N-1个变量对应的二进制码作同样的操作，得到新个体从而得到新种群TP＝TNew，规模仍为Pop。转到步骤2.2继续计算。(3)基于牛顿法的天然气系统能流计算3.1计算不平衡量执行步骤(1)和步骤(2)，可以获得最优的个体中代表的各节点压力，即较好的牛顿法初值。结合式(5)至式(10)，计算出个体中所有节点的不平衡量Δf(k)，即式中，上标k表示的是迭代次数，第一次计算时，k＝1。3.2收敛判据牛顿法计算天然气系统能流的收敛判据是：max(|Δf(k)|)≤ε(ε为牛顿法收敛精度，在步骤1.2已给出)。若满足收敛条件，则转至步骤3.5；若不满足收敛条件，则继续执行步骤3.3。3.3计算雅克比矩阵计算雅克比矩阵J(k),即式中所有变量含义与式(9)和式(11)相同。3.4计算修正量根据步骤3.1和步骤3.3计算的不平衡量Δf(k)和雅克比矩阵J(k)，可以计算N个节点注入压力的修正量，如下所示：ΔΠ(k)＝-[J(k)]-1Δf(k)(37)然后更新各节点压力，公式如下：Π(k+1)＝Π(k)+ΔΠ(k)(38)转到步骤3.1继续计算。3.5计算天然气系统能流分布根据公式(7)至式(10)，计算出管道的流量，压缩机流量以及压缩机消耗的流量，以此得到天然气系统的能流分布。附图说明图1为本发明方法的程序流程框图；图2为本发明方法的步骤(2)中遗传算法初值优选流程图；图3为本发明方法的步骤(3)中基于牛顿法的天然气系统能流计算流程框图；图4为本发明方法中网络结构图。具体实施方式如附图4所示，以14节点天然气系统为例，一种天然气系统能流计算的改进方法具体步骤如下：(1)输入基础数据及初始化1.1输入基础数据首先，输入网络结构数据。具体包括：气源参数、输气管道参数、压缩机参数、气负荷、平衡节点压力以及待求节点压力范围。1.2参数初始化设置遗传算法的交叉概率PC＝0.8，变异概率Pm＝0.3，变量精度esp＝10-4，种群规模Pop＝200，；牛顿法收敛精度ε＝10-6，牛顿法的最大迭代次数iterNWmax＝50。网络数据采用2015年第35卷第24期《中国电机工程学报》中“电-气混联综合能源系统概率能量流分析”一文中的14节点天然气系统的数据，并作如下改进：1)原节点1、9和11的压力分别改为900Psia、1000Psia和1200Psia；2)原节点10的气源供气量为80MMCFD，压力未知；3)原节点2、3、7、8、12、13和14的气负荷分别改为25MMCFD、65MMCFD、25MMCFD、40MMCFD、50MMCFD、70MMCFD和105MMCFD；4)原压缩机#1和#2的压缩比分别改为1.3和1.4。5)节点压力Π2，Π3，Π4的压力范围为600Psia～900Psia，Π6的压力范围为600Psia～1000Psia，Π10，Π12，Π13，Π14的压力范围为800Psia～1000Psia，另外需要解释的是：节点1、9和114给定，节点5和节点7可由压缩机的压缩比控制。(2)基于遗传算法的初值优选2.1编码并产生初始种群第(1)步完成后，根据变量范围和变量精度，按照技术方案中的公式(1)，确定以节点压力为决策变量的二进制串长度，其中14节点天然气系统的状态变量为Π2，Π3，Π4，Π6，Π8，Π10，Π12，Π13，Π14，将其重新编号为：Π1，Π2，Π3，Π4，Π5，Π6，Π7，Π8，Π9，则各变量对应的二进制串长为：确定各变量二进制串长度后，按照公式(2)确定个体染色体的串长度为：根据步骤2.1，利用Matlab产生二进制编码矩阵TP，以第一个个体为例，其二进制码携带9个变量的信息，各个变量对应的二进制码为：TP1_1＝000111100011000010001(41)TP1_2＝001011001101100110110(42)TP1_3＝0111101110100101111110(43)TP1_4＝0001011101101011011101(44)TP1_5＝0000000010001011111010(45)TP1_6＝001000101111001010110(46)TP1_7＝110011001010111111000(47)TP1_8＝000000111010110101010(48)TP1_9＝100110110010110111001(49)2.2译码并得变量的实际值对所得变量进行译码，以第一个个体为例，按照技术方案中的公式，得二进制码对应的十进制数值如下：(TP1_1)D＝0·221-1+0·221-2+…+1·20＝247313(50)(TP1_2)D＝0·221-1+0·221-2+…+0·20＝367414(51)(TP1_3)D＝0·222-1+1·222-2+…+0·20＝2025854(52)(TP1_4)D＝0·222-1+0·222-2+…+1·20＝383709(53)(TP1_5)D＝0·222-1+0·222-2+…+0·20＝8954(54)(TP1_6)D＝0·221-1+0·221-2+…+0·20＝286294(55)(TP1_7)D＝1·221-1+1·221-2+…+0·20＝1676792(56)(TP1_8)D＝0·221-1+0·221-2+…+0·20＝30122(57)(TP1_9)D＝1·221-1+0·221-2+…+1·20＝1271225(58)按照技术方案中的公式(3)，将其二进制编码转换为对应的实际值如下:2.3计算目标函数值根据步骤2.2将种群中每一个体每一变量对应的二进制码转化为对应的实际值，然后计算每一个体对应的目标函数值，即不平衡量总和。以第一个个体为例，其目标函数值为：F(Π1)＝1126.4670(68)2.4收敛判据计算出每一个个体对应的目标函数Fm(Π)，比较目标函数的大小，选出其中的最小值minF(Π)。遗传算法的收敛条件是，若minF(Π)≤90，则满足收敛条件，将minF(Π)对应的个体中的每个变量作为已知量，代入步骤(3)；若不满足收敛条件，即继续执行步骤2.5，直至满足收敛条件为止。得到满足条件的各节点压力值为：Π1＝723.5856Π2＝735.0393Π3＝744.9004Π4＝627.4450Π5＝600.8539(69)Π6＝827.3031Π7＝959.9114Π8＝802.8727Π9＝921.23352.5产生新个体2.5.1选择先根据技术方案中的公式(14)，计算每个个体的适应度函数之，然后按照技术方案中的公式(15)，计算个体的选择概率P(fk)，将所有个体的选择概率用矩阵P表示如下：2.5.2交叉按照技术方案中步骤2.5.2，以第一个体和第二个个体为例，交叉后其变量的二进制编码分别为和数值如下：2.5.3变异对子代种群Tson进行变异操作得到新种群TP＝TNew，以第一个个体为例，变异后其变量的二进制编码分别为得到变异后的新种群之后，将其按照技术方案中的步骤(3)继续进行计算，直至满足收敛要求。(3)基于牛顿法的天然气系统能流计算3.1计算不平衡量以牛顿法第一次迭代后的结果为例，按照技术方案中的公式(12)，计算不平衡量Δf(1)如下：3.2收敛判据当不平衡量Δf(k)满足max(|Δf(k)|)＜ε，则结束迭代计算，输出结果；当max(|Δf(k)|)＞ε且迭代次数k≥iterNWmax，则停止迭代，输出“不收敛！”，结束判断；当max(|Δf(k)|)＞ε且迭代次数k<iterNWmax，则执行步骤3.3，并增加迭代次数，k＝k+1，重新进行迭代计算，直到满足收敛条件。根据前面步骤，迭代6次后即满足收敛条件，此时max(|Δf(k)|)＝1.1232e-7＜ε。3.3计算雅克比矩阵以牛顿法第一次迭代后的结果为例，按照技术方案中的公式(17)，计算雅克比矩阵J(1)3.4计算修正量以牛顿法第一次迭代后的结果为例，按照技术方案中的公式(18)，计算修正量ΔΠ(1)。按照技术方案中的公式(19)更新节点压力3.5计算天然气系统能流分布根据技术方案的公式(7)至式(10)，可以计算出管道的流量，压缩机流量以及压缩机消耗的流量。计算结果如表1和表2所示：表114节点天然气系统管道流量表2压缩机流量和消耗气量实验效果以附图4所示的14节点天然气系统为仿真对象，从收敛特性方面对比所提的遗传-牛顿混合方法和常规牛顿法，以此来验证本发明方法的有效性。常规牛顿法的初值选取方法参考2012年27卷第4期《IEEETransactionsonPowerSystems》中“Aunifiedgasandpowerflowanalysisinnaturalgasandelectricitycouplednetworks”的选取方法，即以天然气系统平衡节点压力作为参考，按天然气管道首、末两端压力差为5％-10％来选取节点压力的初值。所选初值如表3所示：表314节点天然气系统节点压力初值收敛精度为10-4的情况下，上述算例计算完成后得到的收敛特性结果如表4所示：表4遗传-牛顿混合方法与常规牛顿法的比较从表4可看出，与常规牛顿法相比，所提出方法有效地解决了牛顿法在天然气系统能流计算中初值难以选取的问题。为验证本发明方法的有效性和正确性，将仅考虑负荷功率不确定性(方案1)得到的网损可能性分布与本文提出的同时考虑负荷功率不确定性和阻抗不确定性(方案2)得到的网损可能性分布结果对比如表4所示。当前第1页1 2 3