一种海洋中尺度涡的识别方法和装置与流程

本申请涉及海洋遥感领域，更具体地说，涉及一种海洋中尺度涡的识别方法和装置。

背景技术：

中尺度涡，是海洋中的一种涡流，各大洋中都有这种涡流的存在。它们与海洋中大而稳定的环流相比，是尺度较小的海水运动，并不显著，但中尺度涡对全球海洋水量分配、能量与热量的传输有重要作用，对台风路径及其强度的变化乃至全球气候变化都有重大影响，因而对中尺度涡的高效识别已成为当务之急。

现有的效率较高的中尺度涡识别主要采用基于海平面高度异常数据矩阵的闭合等值线法，在传统方法中由于没有深入挖掘海平面高度异常数据矩阵中各个像元之间的相关性，因而后续的闭合等值线的划分和筛选过程比较繁琐且容易出现误判，造成中尺度涡的识别精度低。

技术实现要素：

有鉴于此，本申请提供一种海洋中尺度涡的识别方法和装置，以提高中尺度涡的识别精度。

为了实现上述目的，现提出的方案如下：

一种海洋中尺度涡识别方法，包括：

建立海平面高度异常数据和变差场的原始数据矩阵；

依次将所述原始数据矩阵中各个像元作为预先建立的滑动窗口的中心点；

计算所述滑动窗口内最大像元和最小像元的差的绝对值；

当所述绝对值在预设变差阈值范围内时，将第一赋值赋予所述中心点对应的所述变差场数据矩阵的像元，当所述绝对值不在所述预设变差阈值范围内时，将第二赋值赋予所述中心点对应的所述变差场数据矩阵的像元，为海平面高度异常数据的变差场数据矩阵(空矩阵)赋值；

其中，所述预设变差阈值和所述第一赋值根据所述原始数据矩阵确定；

所述第二赋值的计算公式为：

表示第二赋值，DN_i表示所述中心点对应的所述原始数据矩阵的像元，表示距离所述中心点像元滞后h₀个像元的像元，像元滞后距离h₀为预设值；

基于趋势面分析法，确定所述变差场数据矩阵的趋势分量和剩余分量；

对所述剩余分量进行简单克里金插值处理，并将经过简单克里金插值处理后的剩余分量与所述趋势分量相加，得到经泛克里金插值的中尺度涡识别矩阵；

按照预设识别方法，基于所述中尺度涡识别矩阵对中尺度涡进行识别。

优选的，所述建立海平面高度异常数据的原始数据矩阵，包括：

获取海平面高度异常数据；

对所述海平面高度异常数据进行中值滤波处理以及对所述海平面高度异常数据中的空值进行替换处理；

利用处理后的所述海平面高度异常数据构建所述原始数据矩阵。

优选的，所述滑动窗口的建立过程包括：

在预设采样周期内，获取多组海平面高度异常数据；

建立每组海平面高度异常数据各自对应的原始数据矩阵；

确定各个所述原始数据矩阵对应的实验变差函数；

所述实验变差函数的计算公式为：

其中，所述γ(h)为实验变差函数值，N(h)表示所述海平面高度异常数据的原始数据矩阵中相距h个像元的像元的对数，DN_(i,j)表示海平面高度异常数据的原始数据矩阵中第i行第j列的像元的像元值，和DN(_i+h,j+h)表示海平面高度异常数据原始数据矩阵中第i+h行第j+h列的像元的像元值；

分别对所有所述原始数据矩阵对应的实验变差函数进行求导计算，确定每个原始数据矩阵实验变差函数之导数的最小零点处h值；

计算所有最小零点处h值的平均值，将所述平均值作为所述像元滞后距离h₀；

基于所述像元滞后距离h₀建立所述滑动窗口，其中所述滑动窗口的边长为2h₀。

优选的，所述预设变差阈值为[μ-σ,μ+σ]；

所述第一赋值为：(μ-4σ)；

其中，μ为所述原始数据矩阵平均值，σ为所述原始数据矩阵的标准差。

优选的，所述对所述剩余分量进行简单克里金插值处理，并将经过简单克里金插值处理后的剩余分量与所述趋势分量相加，得到经泛克里金插值的中尺度涡识别矩阵，包括：

确定所述变差场数据矩阵的实验变差函数；

所述实验变差函数的计算公式为：

其中，所述γ(h)为实验变差函数值，N(h)表示所述变差场数据矩阵中相距h个像元的像元的对数，DN(_i,j)表示变差场数据矩阵中第i行第j列的像元的像元值，和DN(_i+h,j+h)表示变差场数据矩阵中第i+h行第j+h列的像元的像元值；

基于预设算法对所述实验变差函数进行计算，确定所述实验变差函数的块金、变程以及偏基台值；

将所述实验变差函数的块金、变程以及偏基台值代入理论变差函数模型中，以实现实验变差函数与理论变差函数模型的拟合；

按照简单克里金插值算法，利用拟合后的理论变差函数模型对所述剩余分量进行插值，再将经过插值的剩余分量与趋势分量相加，实现完整的泛克里金算法。

一种海洋中尺度涡识别装置，包括：

原始数据矩阵建立单元，用于建立海平面高度异常数据的原始数据矩阵；

变差场数据矩阵建立单元，用于建立与海平面高度异常数据原始数据矩阵同行同列数的变差场数据矩阵，通过对海平面高度异常数据原始数据矩阵的变差计算，为变差场数据矩阵赋值。

本单元包括：

依次将所述原始数据矩阵中各个像元作为预先建立的滑动窗口的中心点；

计算所述滑动窗口内最大像元和最小像元的差的绝对值；

当所述绝对值在预设变差阈值范围内时，将第一赋值赋予所述中心点对应的所述变差场数据矩阵的像元，当所述绝对值不在所述预设变差阈值范围内时，将第二赋值赋予所述中心点对应的所述变差场数据矩阵的像元，为海平面高度异常数据的变差场数据矩阵(空矩阵)赋值；

其中，所述预设变差阈值和所述第一赋值根据所述原始数据矩阵确定；

所述第二赋值的计算公式为：

表示第二赋值，DN_i表示所述中心点对应的所述原始数据矩阵的像元，表示距离所述中心点的像元滞后h₀个像元的像元，像元滞后距离h₀为预设值；

泛克里金插值处理单元，用于在趋势面分析法的基础上，确定所述变差场数据矩阵的趋势分量和剩余分量；对所述剩余分量进行简单克里金插值处理，并将经过简单克里金插值处理后的剩余分量与所述趋势分量相加，得到经泛克里金插值的中尺度涡识别矩阵；

中尺度涡识别单元，用于按照预设识别方法，基于所述中尺度涡识别矩阵对中尺度涡进行识别。

优选的，所述原始数据矩阵建立单元包括：

数据采集模块，获取海平面高度异常数据；

数据处理模块，用于对所述海平面高度异常数据进行中值滤波处理以及对所述海平面高度异常数据中的空值进行替换处理，并利用处理后的所述海平面高度异常数据构建所述原始数据矩阵。

优选的，所述变差场数据矩阵建立单元包括：

滑动窗口建立模块，用于在预设采样周期内，获取多组海平面高度异常数据，建立每组海平面高度异常数据各自对应的原始数据矩阵，确定各个所述原始数据矩阵对应的实验变差函数；

所述实验变差函数的计算公式为：

其中，所述γ(h)为实验变差函数值，N(h)表示所述海平面高度异常数据的原始数据矩阵中相距h个像元的像元的对数，DN_(i,j)表示海平面高度异常数据的原始数据矩阵中第i行第j列的像元的像元值，和DN(_i+h,j+h)表示海平面高度异常数据原始数据矩阵中第i+h行第j+h列的像元的像元值；

分别对所有所述原始数据矩阵对应的实验变差函数进行求导计算，确定每个原始数据矩阵实验变差函数之导数的最小零点处h值；

计算所有最小零点处h值的平均值，将所述平均值作为所述像元滞后距离h₀；

基于所述像元滞后距离h₀建立所述滑动窗口，其中所述滑动窗口的边长为2h₀；

变差计算模块，用于依次将所述原始数据矩阵中各个像元作为预先建立的滑动窗口的中心点；

计算所述滑动窗口内最大像元和最小像元的差的绝对值；

当所述绝对值在预设变差阈值范围内时，将第一赋值赋予所述中心点对应的所述变差场数据矩阵的像元，当所述绝对值不在所述预设变差阈值范围内时，将第二赋值赋予所述中心点对应的所述变差场数据矩阵的像元，为海平面高度异常数据的变差场数据矩阵(空矩阵)赋值。

优选的，所述预设变差阈值为[μ-σ,μ+σ]；

所述第一赋值为：(μ-4σ)；

其中，μ为所述原始数据矩阵平均值，σ为所述原始数据矩阵的标准差。

优选的，所述泛克里金插值处理单元包括：

趋势面分析模块，用于基于趋势面分析法，确定所述变差场数据矩阵的趋势分量和剩余分量；

泛克里金插值计算模块，用于确定所述变差场数据矩阵剩余分量的实验变差函数，进而将实验变差函数拟合为理论变差函数，使用理论变差函数对变差场数据矩阵的剩余分量进行简单克里金插值；

本模块包括：

所述实验变差函数的计算公式为：

其中，所述γ(h)为实验变差函数值，N(h)表示所述变差场数据矩阵中相距h个像元的像元的对数，DN(_i,j)表示变差场数据矩阵中第i行第j列的像元的像元值，和DN(_i+h,j+h)表示变差场数据矩阵中第i+h行第j+h列的像元的像元值；

基于预设算法对所述实验变差函数进行计算，确定所述实验变差函数的块金、变程以及偏基台值；

将所述实验变差函数的块金、变程以及偏基台值代入理论变差函数模型中，以实现实验变差函数与理论变差函数模型的拟合；

按照简单克里金插值算法，利用拟合后的理论变差函数模型对所述剩余分量进行插值，再将经过插值的剩余分量与趋势分量相加，实现完整的泛克里金算法。

经由上述技术方案可知，本申请公开了一种海洋中尺度涡识别方法和装置。首先建立海平面高度异常数据的原始数据矩阵，进而对该原始数据矩阵进行处理以获得该原始数据矩阵对应的变差场数据矩阵。进一步，利用趋势面分析法对该变差场数据矩阵进行分析，以进行泛克里金插值计算，从而建立可高度识别中尺度涡的中尺度涡识别矩阵。与现有技术相比，本发明基于海平面高度异常数据矩阵中各个像元之间的相关性，建立了海平面高度异常数据的变差场数据矩阵，并对该变差场数据矩阵进行泛克里金插值处理，因而提高了中尺度涡的识别精度。

附图说明

为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例或现有技术描述中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据提供的附图获得其他的附图。

图1示出了本发明一个实施例公开的一种海洋中尺度涡识别方法的流程示意图；

图2可知，本申请另一个实施例公开一种滑动窗口的创建方法的流程示意图；

图3示出了本发明另一个实施例公开的一种泛克里金插值算法的流程示意图；

图4示出了本发明另一个实施例公开的一种海洋中尺度涡识别装置的结构示意图。

具体实施方式

下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。

图1示出了本发明一个实施例公开的一种海洋中尺度涡识别方法的流程示意图。

由图1可知，在本实施例中，该方法包括：

S101：建立海平面高度异常数据的原始数据矩阵和与原始数据矩阵同行同列的空矩阵。

具体包括：

获取海平面高度异常数据，进而为了避免后续的变差运算放大数据中原有噪声，需要对该海平面高度异常数据集进行中值滤波处理。

需要说明的是，在实际应用中由于海洋中存在陆地、岛屿等区域，上述海平面高度异常数据中存在空值，因而在数据处理时，计算全部有效海平面高度异常数据的均值，将其赋给陆地、岛屿、0-200m深度浅海区域的像元，作为空值的替代值，避免后续程序在运算时发生数值错误。

S102：依次将所述原始数据矩阵中各个像元作为预先建立的滑动窗口的中心点，计算所述滑动窗口内最大像元和最小像元的差的绝对值。

利用预先建立的滑动窗口遍历原始数据矩阵中各个像元。具体的，依次将各个像元作为该滑动窗口的中心点。进而，计算滑动窗口中最大像元和最小像元的差的绝对值。

S103：当所述绝对值在预设变差阈值范围内时，将第一赋值赋予所述中心点对应的空矩阵的像元，当所述绝对值不在所述预设变差阈值范围内时，将第二赋值赋予所述中心点对应的所述空矩阵的像元，以建立海平面高度异常数据的变差场数据矩阵。

其中，该预设变差阈值以及第一赋值可由原始数据矩阵确定。具体的，[μ-σ,μ+σ]；

所述第一赋值为：(μ-4σ)；

其中，μ为所述原始数据矩阵平均值，σ为所述原始数据矩阵的标准差。

所述第二赋值的计算公式为：

表示第二赋值，DN_i表示所述中心点对应的所述原始数据矩阵的像元，表示距离所述中心点的像元滞后h₀个像元的像元，像元滞后距离h₀为预设值。

S104：基于趋势面分析法，确定所述变差场数据矩阵的趋势分量和剩余分量。

趋势面是一种基于空间坐标的低阶多项式，它是一种光滑的数学曲面，能集中地反映空间数据在大范围内的变化趋势。该曲面与实际的空间数据曲面不同，它只是实际曲面的一个近似值。因此实际曲面应包括趋势面和剩余曲面两部分，即

实际曲面＝趋势面+剩余曲面

趋势面反映了区域性的变化规律，它受大范围的系统性因素所控制；剩余曲面则反映了局部变化特点，它受局部因素和随机因素所制约。由此可见，这两部分具有不同性质，趋势面对应于一个确定性函数，而剩余曲面则对应于一个随机函数，即

数据场中各点的真实值＝确定性函数值+随机函数值＝趋势分量+剩余分量

依据上述分析，海平面高度异常数据的变差场数据矩阵可被分解为趋势分量与剩余分量两部分，也就是

Z(P_i)＝Trend(P_i)+R(P_i)(i＝1,2,...,n)。

其中，Trend(P_i)表示趋势分量，R(P_i)为剩余分量。

S105：对所述剩余分量进行简单克里金插值处理，并将经过简单克里金插值处理后的剩余分量与所述趋势分量相加，得到经泛克里金插值的中尺度涡识别矩阵。

S106：按照预设识别方法，基于所述中尺度涡识别矩阵对中尺度涡进行识别。

由以上实施例可知，本申请公开了一种海洋中尺度涡识别方法。首先建立海平面高度异常数据的原始数据矩阵，进而对该原始数据矩阵进行处理以获得该原始数据矩阵对应的变差场数据矩阵。进一步，利用趋势面分析法对该变差场数据矩阵进行分析，以进行泛克里金插值计算，从而建立可高度识别中尺度涡的中尺度涡识别矩阵。与现有技术相比，本发明利用海平面高度异常数据矩阵中各个像元之间的相关性，建立了海平面高度异常数据的变差场数据矩阵，并对该变差场数据矩阵进行泛克里金插值处理，因而提高了中尺度涡的识别精度和效率。

参见图2可知，本申请另一个实施例公开一种滑动窗口的创建方法的流程示意图。

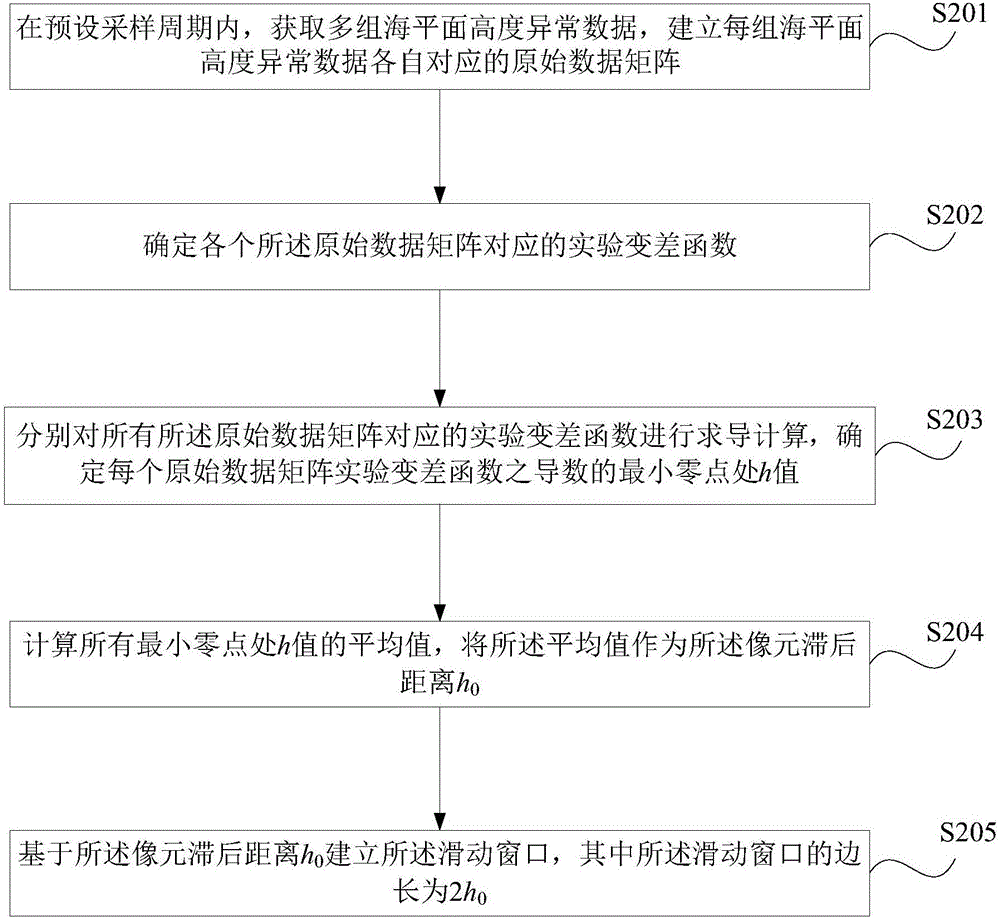
在本实施例中，滑动窗口的建立过程具体包括以下步骤：

S201：在预设采样周期内，获取多组海平面高度异常数据，建立每组海平面高度异常数据各自对应的原始数据矩阵。

在一段采样周期内，获取多组海平面高度异常数据。基于上述多组海平面高度异常数据矩阵建立各自对应的原始数据矩阵。

S202：确定各个所述原始数据矩阵对应的实验变差函数。

所述实验变差函数的计算公式为：

其中，所述γ(h)为实验变差函数值，N(h)表示所述海平面高度异常数据的原始数据矩阵中相距h个像元的像元的对数，DN_(i,j)表示海平面高度异常数据的原始数据矩阵中第i行第j列的像元的像元值，和DN(_i+h,j+h)表示海平面高度异常数据原始数据矩阵中第i+h行第j+h列的像元的像元值；

S203：分别对所有所述原始数据矩阵对应的实验变差函数进行求导计算，确定每个原始数据矩阵实验变差函数之导数的最小零点处h值。

对任意实验变差函数而言，该实验变差函数包括多个导数为零的点，取每个实验变差函数的最小零点处h值。

S204：计算所有最小零点处h值的平均值，将所述平均值作为所述像元滞后距离h₀；

S205：基于所述像元滞后距离h₀建立所述滑动窗口，其中所述滑动窗口的边长为2h₀。

参见图3示出了本发明另一个实施例公开的一种泛克里金插值算法的流程示意图。

由图3可知，该方法包括：

S301：确定所述原始数据矩阵的实验变差函数。

所述实验变差函数的计算公式为：

其中，所述γ(h)为实验变差函数值，N(h)表示所述变差场数据矩阵中相距h个像元的像元的对数，DN(_i,j)表示变差场数据矩阵中第i行第j列的像元的像元值，和DN(_i+h,j+h)表示变差场数据矩阵中第i+h行第j+h列的像元的像元值；

S302：基于预设算法对所述实验变差函数进行计算，确定所述实验变差函数的块金、变程以及偏基台值。

计算h＝0时，实验变差函数γ(h)的值，其中块金C₀＝γ(0)；

进一步对于实验变差函数求导，得到得到函数γ’(h)，设令γ’(h)＝0的h中最小的为h_a，则变程a＝h_a；

设令γ’(h)＝0的h中最大的为h_C，则偏基台值C＝γ(h_C)-C₀；

至此C₀，a，C均已求出。

S303：将所述实验变差函数的块金、变程以及偏基台值代入理论变差函数模型中，以实现实验变差函数与理论变差函数模型的拟合。

本发明中，分别依据球状、指数、高斯和稳定4种模型来拟合变差函数。

A.球状模型

B.指数模型

C.高斯模型

D.稳定模型

S304：按照简单克里金插值算法，利用拟合后的理论变差函数模型对所述剩余分量进行插值，再将经过插值的剩余分量与趋势分量相加，实现完整的泛克里金算法。

分别使用高斯、指数、球状和稳定4种模型对变差场数据矩阵剩余值进行插值，插值过程如下：

视变差场数据矩阵为区域化变量，n个已知数据点P_i的DN值分别为Z(P_i)(i＝1,2,…n)。趋势面分析可知，变差场数据矩阵由Trend(P_i)和R(P_i)两部分组成，而R(P_i)＝Z(P_i)-Trend(P_i)，故在此步骤中实际执行插值的是R(P_i)。待插值点R^*(P₀)值的估计结果如下，

如同其他的空间插值方法一样，普通克里金插值法的根本出发点也是计算代表第i个点P_i的待定权重的W_i，只是其求取权重的手段与其他插值方法有所不同。克里金插值法采用权重方程组求解权重。权重方程组形如

式中γ(P_i,P_k)表示相距h的点P_i与P_k之间的变差函数值γ(h)，γ(h)即4种理论变差函数模型其一，c表示已知常数。

对R(P_i)进行上述的简单克里金插值得到R’(P_i)，再与趋势分量Trend(P_i)重新相加即获取最终插值结果：

Z'(P_i)＝Trend(P_i)+R'(P_i) (i＝1,2,...,n)

其中Z’(Pi)表示泛克里金插值的输出结果。

S305：对泛克里金插值结果进行交叉验证。

需进行交叉验证以确定插值精度是否符合要求。

交叉验证是这样实现的：首先移除变差场数据矩阵插值结果中的一个数据点，用剩余的所有点去插值(仍然使用上述4种模型其一)，得到这个被移除点位置的值，将此预测值与其真实值比较，依此类推，当此方法在所有的点上实施之后，变差场数据矩阵插值结果中每个数据点都具有一个预测值和一个真实值，如此，即可使用下面5个指标来计算交叉验证结果(表1)。

表1交叉验证参数计算式

(Z^*(P_i)表示P_i点估计值，Z(P_i)表示P_i点观察值，σ_k²(P_i)表示P_i位置处克里金方差)

在本发明中，首先从变差场数据矩阵插值结果的全部已知数据点中取出一个用来比较的数据子集和用来插值的数据子集(两子集不可有交集)，方法是先将变差场数据矩阵插值结果进行降低分辨率的重采样，如对于m×n(m行n列)的变差场数据矩阵插值结果而言，可将行数和列数均缩减为原始值的1/4实现重采样，即将其变为的点阵，作为用来比较的数据子集，而把原始变差场数据矩阵插值结果数据点用作进行插值的数据子集，如此，在使用后者完成插值后，就可以将插值结果与用来比较的数据子集进行比较，得到所需的各种交叉验证参数(ME、MSE、RMSE、ASE和RMSSE)。

若交叉验证参数值符合以下标准(表2)，则认为选取的理论变差函数模型符合要求，从而进一步在4种模型中按照此标准挑选1个最佳模型作为最终的插值模型，完成泛克里金插值。

表2交叉验证得数评价表

参见图4示出了本发明另一个实施例公开的一种海洋中尺度涡识别装置的结构示意图。

由图4可知，在本实施例中，该装置包括：原始数据矩阵建立单元1、变差场数据矩阵建立单元2、泛克里金插值处理单元3以及中尺度涡识别单元4。

其中，

原始数据矩阵建立单元1用于建立海平面高度异常数据的原始数据矩阵。

具体的，该所述原始数据矩阵建立单元1包括：数据采集模块11以及数据处理模块12。

数据采集模块11用于获取海平面高度异常数据，并将采集到的海平面高度异常数据发送至数据处理模块12中。

数据处理模块12对所述海平面高度异常数据进行中值滤波处理以及对所述海平面高度异常数据中的空值进行替换处理，并利用处理后的所述海平面高度异常数据构建所述原始数据矩阵。

变差场数据矩阵建立单元2用于基于所述原始数据矩阵建立与其同行同列数的海洋高度异常数据的变差场数据矩阵。

具体的，所述变差场数据矩阵建立单元2包括：滑动窗口建立模块21和数据计算模块22。

其中，滑动窗口建立模块21具体用于在预设采样周期内，获取多组海平面高度异常数据，建立每组海平面高度异常数据各自对应的原始数据矩阵，确定各个所述原始数据矩阵对应的实验变差函数；

进而，分别对所有所述原始数据矩阵对应的实验变差函数进行求导计算，确定每个原始数据矩阵实验变差函数之导数的最小零点处h值；

计算所有最小零点处h值的平均值，将所述平均值作为所述像元滞后距离h₀；并将2h₀作为滑动窗口的边长以建立滑动窗口。

数据计算模块用于首先建立一个与原始数据矩阵同行同列的空矩阵，进而依次将所述原始数据矩阵中各个像元作为滑动窗口的中心点，计算所述滑动窗口内最大像元和最小像元的差的绝对值。

当所述绝对值在预设变差阈值范围内时，将第一赋值赋予所述中心点对应的所述空矩阵的像元，当所述绝对值不在所述预设变差阈值范围内时，将第二赋值赋予所述中心点对应的所述空矩阵的像元以建立海平面高度异常数据的变差场数据矩阵(。

其中，预设变差阈值为[μ-σ,μ+σ]；所述第一赋值为：(μ-4σ)；

μ为所述原始数据矩阵平均值，σ为所述原始数据矩阵的标准差

所述第二赋值的计算公式为：

表示第二赋值，DN_i表示所述中心点对应的所述原始数据矩阵的像元，表示距离所述中心点滞后h₀个像元的像元，像元滞后距离h0为预设值。

泛克里金插值处理单元3包括：趋势面分析模块31和泛克里金插值计算模块32。

趋势面分析模块，用于以趋势面分析法为基础，确定所述变差场数据矩阵的趋势分量和剩余分量。

泛克里金插值计算模块，用于确定所述变差场数据矩阵剩余分量的实验变差函数；

基于预设算法对所述实验变差函数进行计算，确定所述实验变差函数的块金、变程以及偏基台值；

将所述实验变差函数的块金、变程以及偏基台值代入理论变差函数模型中，以实现实验变差函数与理论变差函数模型的拟合；

进而，使用简单克里金插值算法，利用拟合后的理论变差函数模型对所述剩余分量进行插值，再将经过插值的剩余分量与趋势分量相加，实现完整的泛克里金算法并得到经泛克里金插值的中尺度涡识别矩阵。

中尺度涡识别单元4，用于按照预设识别方法，基于所述中尺度涡识别矩阵对中尺度涡进行识别。

需要说明的是该装置实施例与方法实施例相对应，其执行过程和执行原理相同，在此不作赘述。

最后，还需要说明的是，在本文中，诸如第一和第二等之类的关系术语仅仅用来将一个实体或者操作与另一个实体或操作区分开来，而不一定要求或者暗示这些实体或操作之间存在任何这种实际的关系或者顺序。而且，术语“包括”、“包含”或者其任何其他变体意在涵盖非排他性的包含，从而使得包括一系列要素的过程、方法、物品或者设备不仅包括那些要素，而且还包括没有明确列出的其他要素，或者是还包括为这种过程、方法、物品或者设备所固有的要素。在没有更多限制的情况下，由语句“包括一个……”限定的要素，并不排除在包括所述要素的过程、方法、物品或者设备中还存在另外的相同要素。

本说明书中各个实施例采用递进的方式描述，每个实施例重点说明的都是与其他实施例的不同之处，各个实施例之间相同相似部分互相参见即可。

对所公开的实施例的上述说明，使本领域专业技术人员能够实现或使用本发明。对这些实施例的多种修改对本领域的专业技术人员来说将是显而易见的，本文中所定义的一般原理可以在不脱离本发明的精神或范围的情况下，在其它实施例中实现。因此，本发明将不会被限制于本文所示的这些实施例，而是要符合与本文所公开的原理和新颖特点相一致的最宽的范围。