一种高精度的传递函数采样方法与流程

本发明属于机械系统结构动力学振动计算与分析相关技术领域，更具体地，涉及一种高精度的传递函数采样方法。

背景技术：

传递函数分析是机械系统动力学分析中的重要环节，是机械系统固有特性的表征，机械系统受激振动的响应特性只与激励的性质及系统激励-响应点间的传递特性(传递函数)有关。通过获取不同传递途径下系统传递函数的幅频特性图和相频特性图，可以揭示系统在不同频域带宽内的响应特性，以对系统进行实时评估，因此，传递函数分析在机械系统的设计、评估、结构改进以及模型修正、修改等过程中有重要的作用。

传递函数的获取方法有两种：第一种是通过实验进行传递函数的测量获取；第二种是先建立系统的等效动力学模型，再通过传递函数的理论计算与分析方法获得。

在传递函数特性曲线中(以幅频图为例)，其核心的内容为传递函数中共振峰的频率以及共振峰对应的幅值，传递函数共振峰频率与系统模态频率间有着必然联系。目前，国内外通用的各种机械系统多体动力学软件(以ADAMS为例)在传递函数计算与分析过程中，所采取的采样方法主要有简单的线性频率分布及对数频率分布两种。用户设置传递函数显示带宽的开始频率、截止频率以及频率点数之后，通过选取线性等分(linear spacing of steps)或者对数等分(logarithmic spacing of steps)的频率采样方式以得到固定的一组频率序列，软件经计算及采样过程后，能够得到用户指定输入通道-输出通道间离散数据的传递函数曲线。但是，由于并未考虑到传递函数共振峰频率与系统模态频率的特殊关系，在相同采样方式下，不同的采样频率(采样点数)会对最终传递函数计算结果曲线有很大影响，当采样频率过低即采样点数较少时，无论是线性采样方式还是对数采样方式，均会产生共振频率移位、共振幅值过低的现象，甚至在某些极端情况下，部分传递函数共振峰会因为采样频率过低而直接被遗漏：如重叠峰值(或相近峰)出现漏采的情况，精度较低，不利于对系统的计算及评估。相应地，本领域存在着发展一种精度较高的传递函数采样方法的技术需求。

技术实现要素：

针对现有技术的以上缺陷或改进需求，本发明提供了一种高精度的传递函数采样方法，其结合系统模态分析的数据(模态频率)，在低频率条件下，通过细化采样以增加可能共振点(即系统模态频率点)附近采样数据点的密集程度，在总采样点数少量增加的情况下高精度的获取了传递函数最重要的特征、共振频率点以及共振峰值，有利于机械系统结构动力学振动计算与分析。

为实现上述目的，本发明提供了一种高精度的传递函数采样方法，其包括以下步骤：

(1)构建机械系统的动力学方程；

(2)通过系统振动模态计算方法得到系统振动频率；

(3)设置采样方式、采样带宽及采样点数以生成基础传递函数采样频率点序列；

(4)提取处于传递函数分析带宽内的模态频率及设置每阶模态频率对应细化采样点数的总数目，以形成传递函数分析带宽内的模态频率对应的细化采样点序列；

(5)将基础传递函数采样频率点序列与细化采样点序列合并以生成最终的传递函数采样频率点序列；

(6)对最终的传递函数采样频率点序列进行传递函数数值计算以得到最终离散数据的传递函数图。

进一步的，所述基础传递函数采样频率点序列与所述细化采样点序列合并后，通过按从小到大的顺序排列来生成所述的最终的传递函数采样频率点序列。

进一步的，所述基础传递函数采样频率点序列为ω₁、ω₂、ω₃、...、ω_k、...、ω_M。

其中，

ω_start为带宽起始频率点，ω_end为带宽截止频率点，M为总采样点数。

进一步的，所述细化采样点序列为：

ω_d11、ω_d12、...、ω_d1j、...、ω_d1p、...、ω_di1、ω_di2、...、ω_dij、...、ω_dip、...(i＝1,2,...,m)

其中，p为对应每阶模态频率点前后细化采样点的总数目，其作用是在每阶模态频率点前后按指定规则生成p个细化采样点，以避免因采样频率过低而产生较大的传递函数误差；系统N阶模态频率中的m阶模态频率处于传递函数分析带宽内。

总体而言，通过本发明所构思的以上技术方案与现有技术相比，本发明较佳实施方式提供的高精度的传递函数采样方法，其结合系统模态分析的数据(模态频率)，在低频率条件下，通过细化采样以增加可能共振点(即系统模态频率点)附近采样数据点的密集程度，在总采样点数少量增加的情况下高精度的获取了传递函数最重要的特征、共振频率点以及共振峰值，有利于机械系统结构动力学振动计算与分析。

附图说明

图1是本发明较佳实施方式提供的高精度的传递函数采样方法的流程图。

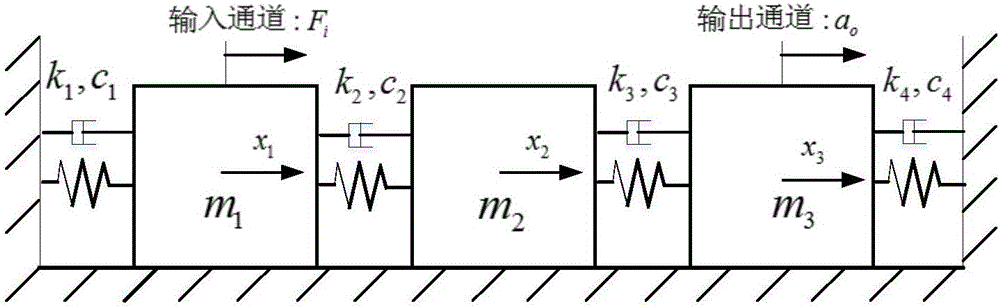
图2是图1中的高精度的传递函数采样方法涉及的三自由度弹簧阻尼-质量系统的示意图。

图3(a)为对数采样方式、采样点数为101时，分别采用本发明的传递函数采样方法与现有方法的获得的输入F_i-输出a_o传递函数幅频曲线的对比图。

图3(b)为对数采样方式、采样点数为101时，分别采用本发明的高精度的传递函数采样方法与现有方法获得的输入F_i-输出a_o传递函数幅频曲线的局部放大对比图(第三峰值区间)。

图3(c)为线性采样方式、采样点数为101时，分别采用本发明的高精度的传递函数采样方法与现有方法获得的输入F_i-输出a_o传递函数幅频曲线的对比图。

图3(d)为线性采样方式、采样点数为101时，分别采用本发明的高精度的传递函数采样方法与现有方法获得的输入F_i-输出a_o传递函数幅频曲线的局部放大对比图(第三峰值区间)。

图4(a)为对数采样方式、采样点数为1001时，分别采用本发明的高精度的传递函数采样方法与现有方法获得的输入F_i-输出a_o传递函数幅频曲线的对比图。

图4(b)为对数采样方式、采样点数为1001时，分别采用本发明的高精度的传递函数采样方法与现有方法获得的输入F_i-输出a_o传递函数幅频曲线的局部放大对比图(第二、三峰值区间)。

图4(c)为线性采样方式、采样点数为1001时，分别采用本发明的高精度的传递函数采样方法与现有方法获得的输入F_i-输出a_o传递函数幅频曲线的对比图。

图4(d)为线性采样方式、采样点数为1001时，分别采用本发明的高精度的传递函数采样方法与现有方法获得的输入F_i-输出a_o传递函数幅频曲线的局部放大对比图(第二、三峰值区间)。

图5(a)为对数采样方式、采样点数分别为101、1001时，采用现有方法获得的输入F_i-输出a_o传递函数幅频曲线的对比图。

图5(b)为对数采样方式、采样点数分别为101、1001时，采用现有方法获得的输入F_i-输出a_o传递函数幅频曲线的局部放大对比图(第二、三峰值区间)。

图5(c)为线性采样方式、采样点数分别为101、1001时，采用现有方法获得的输入F_i-输出a_o传递函数幅频曲线的对比图。

图5(d)为线性采样方式、采样点数分别为101、1001时，采用现有方法获得的输入F_i-输出a_o传递函数幅频曲线的局部放大对比图(第二、三峰值区间)。

图6(a)为对数采样方式、采样点数分别为101、1001时，采用发明的高精度的传递函数采样方法获得的输入F_i-输出a_o传递函数幅频曲线的对比图。

图6(b)为对数采样方式、采样点数分别为101、1001时，采用本发明的高精度的传递函数采样方法获得的输入F_i-输出a_o传递函数幅频曲线的局部放大对比图(第二、三峰值区间)。

图6(c)为线性采样方式、采样点数分别为101、1001时，采用本发明的高精度的传递函数采样方法获得的输入F_i-输出a_o传递函数幅频曲线的对比图。

图6(d)为线性采样方式、样点数分别为101、1001时，采用本发明的高精度的传递函数采样方法获得的输入F_i-输出a_o传递函数幅频曲线的局部放大对比图(第二、三峰值区间)。

具体实施方式

为了使本发明的目的、技术方案及优点更加清楚明白，以下结合附图及实施例，对本发明进行进一步详细说明。应当理解，此处所描述的具体实施例仅仅用以解释本发明，并不用于限定本发明。此外，下面所描述的本发明各个实施方式中所涉及到的技术特征只要彼此之间未构成冲突就可以相互组合。

请参阅图1及图2，本发明较佳实施方式提供的高精度的传递函数采样方法，具体为一种可自动捕捉谐振峰值的非规则采样方法，所述传递函数采样方法可以在相对较低的采样频率设置下显著提高传递函数计算的输出精度，且可广泛应用于各种结构振动特性仿真。

具体地，所述的高精度的传递函数采样方法主要包括以下步骤：

步骤一，构建机械系统的动力学方程。具体地，本实施方式以三自由度弹簧阻尼-质量系统为例对本发明提供的高精度的传递函数采样方法进行说明，三自由度弹簧阻尼-质量系统的参数为：质量块质量分别为m₁＝1kg，m₂＝2kg，m₃＝1kg，弹簧阻尼连接参数分别为k₁＝1×10⁶N/m，c₁＝1N·s/m，k₂＝2×10⁴N/m，c₂＝1N·s/m，k₃＝1×10⁴N/m，c₃＝1N·s/m，k₄＝0.9×10⁶N/m，c₄＝1N·s/m，传递函数计算时输入通道为作用在质量块1上的扫频力信号F_i，输出通道为测量质量块3的振动加速度信号a_o。以质量块的平动位移为广义坐标X＝[x₁ x₂ x₃]^T，则得机械系统的振动方程如下：

其中：

步骤二，通过系统振动模态计算方法得到系统振动频率。具体地，系统振动频率分别为ω_d1、ω_d2、ω_d3、...、ω_di、...、ω_dN。

其中，ω_di为动力学系统第i阶有阻尼振动模态频率，N为系统模态频率总阶数。本实施方式中，对于三自由度弹簧阻尼-质量系统，ω_d1＝19.33Hz、ω_d2＝151.83Hz、ω_d3＝160.75Hz。

步骤三，设置常规传递函数采样方式、采样带宽及采样点数，以生成基础传递函数采样频率点序列。具体地，所述基础传递函数采样频率点序列(以对数等分采样方式为例)为ω₁、ω₂、ω₃、...、ω_k、...、ω_M。

其中：

ω_start为带宽起始频率点，ω_end为带宽截止频率点，M为总采样点数。

本实施方式中，设置采样带宽为1Hz～1000Hz，采样点数为101，常规传递函数采样方式分别为对数频率采样和线性频率采样，则有：

A：对数频率采样

beta＝(lg1000-lg1)/(101-1)＝0.03，ω₁＝1,ω_M＝1000,ω_k＝1×10^(k-1)×0.03Hz

生成基础传递函数采样频率点序列：

ω₁＝1、ω₂＝1.07、...、ω_k＝1×10^(k-1)×0.03、...、ω₁₀₀＝933.25、ω₁₀₁＝1000Hz

B：线性频率采样

beta＝(1000-1)/(101-1)＝9.99，ω₁＝1,ω_M＝1000,ω_k＝(9.99k-8.99)Hz

生成基础传递函数采样频率点序列：

ω₁＝1、ω₂＝10.99、...、ω_k＝(9.99k-8.99)、...、ω₁₀₀＝990.01、ω₁₀₁＝1000Hz

步骤四，设置每阶模态频率点前后细化采样点的总数目，以及提取系统N阶模态频率中处于传递函数分析带宽内的m阶模态频率，得到的细化采样点形成该前m阶模态频率点附近的细化采样点序列。本实施方式中，传递函数分析带宽为待分析的带宽。具体地，所述细化采样点序列为：

ω_d11、ω_d12、...、ω_d1j、...、ω_d1p、...、ω_di1、ω_di2、...、ω_dij、...、ω_dip、...(i＝1,2,...,m)。

其中，p为对应每阶模态频率点前后细化采样点的总数目，其作用是在每阶模态频率点前后按指定规则生成p个细化采样点，以避免因采样频率过低而产生较大的传递函数误差。

本实施方式中采样带宽1～1000Hz内包含系统前三阶固有振动频率(即m＝3)，分别为ω_d1＝19.33Hz、ω_d2＝151.83Hz、ω_d3＝160.75Hz。由于整体采样方式为对数采样，对于每个共振点，在共振频率以及其前后按规律共增加3个细化频率点(即P＝3)，总共生成以下所示的9个点数的细化采样点序列：

ω_d11＝19.05、ω_d12＝19.33、ω_d13＝19.62、ω_d21＝148.06、ω_d22＝151.83、

ω_d23＝155.69、ω_d31＝156.72、ω_d32＝160.75、ω_d33＝164.89

即：[19.05,19.33,19.62,148.06,151.83,155.69,156.72,160.75,164.89]

本实施方式的具体细化采样点关系为ω_di2＝ω_di，

步骤五，将基础传递函数采样频率点序列与细化采样点序列合并，并按从小到大的顺序排列以作为最终的传递函数采样频率点序列。具体地，

A：对数频率采样

[1,1.07,...,18.2,19.05,19.33,19.50,19.62,...,144.54,148.06,151.83,154.88,155.69,156.72,160.75,164.89,...,1000]

B：线性频率采样

[1,10.99,19.05,19.33,19.62,20.98,,...,148.06,150.85,151.83,155.69,156.72,160.75,160.84,164.89,...,1000]

步骤六，通过底层程序模块对最终的传递函数采样序列进行传递函数数值计算，以得到最终离散数据形式的传递函数图。请参阅图3，图3为线性采样方式，采样点数为101时，分别采用本发明较佳实施方式提供的高精度的传递函数采样方法及现有方法获得的多个不同的输入F_i-输出a_o传递函数幅频曲线的对比图。

采用本发明较佳实施方式提供的高精度的传递函数采样方法，分别设置常规传递函数采样方式为对数频率采样和线性频率采样，采样带宽为1Hz～1000Hz，采样点数为1001，得到最终传递函数图。图4为采样点数为1001时，本发明提供的方法与现有方法的输入F_i-输出a_o传递函数幅频曲线的对比图，图4(a)、4(b)为对数采样方式，其中图4(b)为第二、三峰值区间局部放大对比图，图4(c)、4(d)为采用线性采样方式时，分别采用本发明的方法及现有方法获得输入的F_i-输出a_o传递函数幅频曲线的对比图，其中图4(d)为第二、三峰值区间局部放大对比图。

请参阅图5，图5(a)为对数采样方式，采样点数分别为101、1001时，采用现有方法获得的输入F_i-输出a_o传递函数幅频曲线的对比图，图5(b)为采样点数分别为101、1001时，采用现有方法获得的输入F_i-输出a_o传递函数幅频曲线的第二、三峰值区间局部放大对比图。图5(c)、5(d)为采用线性采样方式，采样点数分别为101、1001时，采用现有方法获得的输入F_i-输出a_o传递函数幅频曲线的对比图，其中图5(d)为第二、三峰值区间局部放大对比图。

请参阅图6，图6(a)、6(b)为采用对数采样方式，采样点数分别为101、1001时，采用本发明提供的方法获得的输入F_i-输出a_o传递函数幅频曲线的对比图，其中图6(b)为第二、三峰值区间的局部放大对比图。图6(c)、6(d)为采用线性采样方式，采样点数分别为101、1001时，采用本发明提供的方法获得的输入F_i-输出a_o传递函数幅频曲线对比图，其中图6(d)为第二、三峰值区间局部放大对比图。

根据不同采样方式(对数/线性)，不同采样点数(101/1001)下，分别采用现有采样方法和本发明提供的方法获得的计算结果，对传递函数频带范围内的第一、二、三峰值的频率和幅值误差进行统计，如表1所示。

表1不同采样条件下传递函数误差对比表

自图5(a)、5c)和表1可以看出，现有方法的采样精度与采样频率(或采样点数)的高低有直接关系，在采样频率较低的时候，采样精度差，严重时甚至出现重叠峰遗漏的情况，如当采样点数为101时，相近双峰误采为单峰，且峰值频率和幅值均存在很大误差。同时，对比图5(a)与5(c)，结合表1内的峰值误差数据可以看出，现有采样方法的采样精度也与其采样方式直接相关，当为对数采样方式时，高频区间传递函数的采样精度较低，而当为线性采样方式时，则低频区间传递函数的采样精度相对较低。

通过图6可以看出，相比于现有采样方法，采样方式以及采样频率的高低对于本发明较佳实施方式提供的高精度的传递函数采样方法的采样精度影响较小，无论线性采样方式还是对数采样方式，在低采样频率下，所述的高精度的传递函数采样方法依旧能够比较准确的获取共振峰的频率及幅值，从而达到频响曲线高精度获取的目的。可见，本发明较佳实施方式提供的高精度的传递函数采样方法基本不受采样方式的选择以及采样频率的高低的影响，始终能够提供正确有效的分析结果，提高了采样精度，有利于机械系统结构动力学振动计算与分析。

本发明较佳实施方式提供的高精度的传递函数采样方法，其结合系统模态分析的数据(模态频率)，在低频率条件下，通过细化采样以增加可能共振点(即系统模态频率点)附近采样数据点的密集程度，在总采样点数少量增加的情况下高精度的获取了传递函数最重要的特征、共振频率点以及共振峰值，有利于机械系统结构动力学振动计算与分析。

本领域的技术人员容易理解，以上所述仅为本发明的较佳实施例而已，并不用以限制本发明，凡在本发明的精神和原则之内所作的任何修改、等同替换和改进等，均应包含在本发明的保护范围之内。