基于快速自适应量子遗传算法的复杂井眼轨迹优化方法与流程

本发明涉及先进智能优化算法领域，特别涉及基于快速自适应量子遗传算法的复杂井眼轨迹优化方法。

背景技术：

随着油气田开发技术的不断提高，定向井、超深井、水平井、大位移井、侧钻井、分支井以及多靶井等复杂井眼轨迹类型与日俱增，加之非常规、深水、深层、极地等油气田数量增长。科学的井眼轨迹设计是钻井工程中的关键技术之一。

在井眼轨迹优化中，主要经历的两个阶段：一是将三维井眼轨迹优化问题转化平面上的二维优化问题，采用最优化方法实现二维井眼轨迹的优化；二是采用先进的智能优化算法实现三维井眼轨迹的优化。目前，在三维井眼轨迹优化技术正处于第二个阶段。国内外采用粒子群算法(pso)，改进的粒子群算法(npso)，混合杜鹃搜索优化(hcso)，改进的遗传算法(nga)以及混合蝙蝠飞行优化算法(hbfo)等智能算法实现三维井眼轨迹优化。而现有的算法的效率、稳定性和鲁棒性存在不足，使得优化三维井眼轨迹的实时性较差，优化的结果不够理想。

技术实现要素：

针对在复杂三维井眼轨迹优化问题中自变量多，约束条件复杂的特点，为提高多靶点多井段复杂井眼轨迹优化结果的精度和优化速度，克服现有算法的实时较差的问题，本发明的目的在于提供一种基于快速自适应量子遗传算法(faqga)的复杂井眼轨迹优化方法。

为实现上述目的，本发明技术方案是这样实现的：

基于快速自适应量子遗传算法的复杂井眼轨迹优化方法，包括如下步骤：

(1)生成fibonacci数列，计算fn/fn+x，其中x＝1,2,3…；n为常数；

(2)初始化种群q(t)和设置算法参数：令iteration＝0，随机产生n条染色体组成初始化群体q0(t)；设置量子旋转门转角步长初值和δθ0，变异概率pm，最大迭代次数gen_max＝200；设置faqga的算法参数；

(3)解空间变换，当优化过程限定在单位空间iⁿ＝[-1,1]ⁿ内，在bloch球面坐标中m个量子位有3m个坐标，利用线性变换，将这3m个坐标由n维单位空间iⁿ＝[-1,1]ⁿ映射优化问题的解空间，每个坐标对应解空间中的一个优化变量，第i条染色体qi^t所对应第j个量子位相应的解空间变量为：

式(3)中，和是第j个量子位的bloch坐标值。每条染色体对应优化问题的三个解。bi和ai分别为优化问题解空间的最大值和最小值。

(4)计算目标函数值：针对复杂井眼轨迹优化问题，选择井身实际测量深度tmd(truemeasurementdepth，tmd)为优化目标，对井身、井斜角、井斜方位角以及井段曲率参数优选，以自变量的取值，套管的长度及目标垂直井深为约束条件，目标函数可定义为：

obj_function＝min{tmd}

其中：tmd＝dkop+d1+d2+d3+d4+d5+hd

s.t.xmin≤x≤xmax

casjmin≤casj≤casjmax

tvdmin≤tvd≤tvdmax(4)

式(4)中，x＝(hd,phi1～phi3,theta1～theta6,dd,db,ds1～ds3,dkop)∈r¹⁶，即解空间r¹⁶由16维决策向量x组成，即16为待优化参数的个数；tmd为优化目标函数，ft；j为套管设计的段数。井眼轨迹各段计算公式定义为：

d2＝(dd-dkop-d1×(sinφ1-sinφ0)/(φ1-φ0))/cos(φ1)

(6)

d4＝(db-dd-d3×(sinφ2-sinφ1)/(φ2-φ1))/cos(φ2)

(8)

增斜段曲线长度为：

(10)

式(10)中，r为曲率半径，

式(10)曲线段在三维坐标下的增量计算定义为：

由式(3)～(14)计算目标函数tmd，并保存符合约束条件的最优解，将第一代最优解、最优染色体和最优目标函数值暂存，作为全局最优解global_xb、全局最优染色体global_qb和全局目标函数global_tmd，随着迭代次数的增加，根据式(4)计算目标适应度值tmd(gxb)，记录当代最优解gxb及其最优染色体在符合约束条件下，若tmd(gxb)<tmd(global_xb)，则否则，保持global_qb不变，令iteration＝iteration+1；

(5)计算相邻两代目标函数的相对变化率x：在最优解的搜索过程中，考虑目标函数在搜索点的变化率，建立反映搜索点处的相邻两代目标适应度值相对变化值x，并将该值引入到量子旋转门转角步长的更新策略中，自适应调整算法的搜索方向和收敛速度，提高算法的运行效率，x定义为：

式(15)中，int(.)表示取整运算；x为size行coder列的步长调整矩阵，为目标函数f(x)在点梯度；和分别为相邻两代目标函数值梯度的最大最小值；

(6)量子位的更新，在bloch球面坐标中，采用量子旋转门实现量子位的更新，更新过程定义为：

式(16)中，u为酉矩阵，u的作用是使量子位的相位在xoy平面旋转和延z轴方向旋转δθ。其中和δθ的计算公式定义为：

式(17)中，δφ0和δθ0为单位转角步长，δφ0＝δθ0＝0.05π；sgn(.)为求符号函数。

(7)量子位的变异，在基于bloch球面坐标中，以变异概率为pm随机对若干个量子位执行h逻辑门变异操作，执行过程为：

式(18)实现量子位变异实质是对这若干个量子位的幅角同时逆时针旋转π/4，以保持种群的多样性，降低早熟收敛概率。

(8)判断是否已达到最大迭代次数限制，即iteration<gen_max？若是，则转至(3)；否则，转至(9)；

(9)输出全局最优解global_xb，即输出global_xb＝(hd,phi1～phi3,theta1～theta6,dd,db,ds1～ds3,dkop)；输出全局最优染色体和最优目标函数global_tmd。

本发明采用快速自适应量子遗传算法在bloch球面坐标体系，引入fibonacci数列实现快速自适应调整的转角步长，利用量子遗传算法的超高速、超并行和全局寻优的特点，完成多靶点复杂三维井眼轨迹优化。首先，通过分析fibonacci数列，发现该数列具有负指数特性，将该特性引入到量子旋转门转角步长的更新策略中，从而在不增加算法的空间复杂度的同时降低算法的时间复杂度，大幅提高了算法的效率，缩短算法的运行时间。其次，将任意一个量子位与bloch球面上的点一一对应，从而增加解得遍历性。最后，针对多靶点复杂三维井眼轨迹优化问题，在各井段、套管的长度及目标垂直井深约束条件下，应用faqga优化实际测量井深tmd(truemeasurementdepth，tmd)，完成井身、井斜角、井斜方位角以及井段曲率参数的优选，实现精确、高效的井眼轨迹优化。从而提高钻井效率和成功率，降低钻井时间和钻井成本。

通过分析fibonacci数列发现，该数列第n个数列fn与第n+x数列fn+x数列比值的负指数特性，即g(x)＝(fn/fn+x)|n＝15≈e^-0.4812x，并将该特性引入到量子遗传算法转角步长和δθ的更新策略中，设计了基于bloch球面坐标体系下的快速自适应量子遗传算法faqga，faqga在不增加算法的空间复杂度同时降低算法的时间复杂度，提高算法的效率。即有效的防止搜索过程中的陷入局部最优，又避免了因越过最优点而引起的算法震荡。将faqga用于复杂三维井眼轨迹的实际测量深度tmd的优化，以多靶点的井眼轨迹为研究对象，完成井身、井斜角、井斜方位角以及井段曲率参数的优选，从而完成复杂三维井眼轨迹的设计。采用faqga实现复杂井眼轨迹优化问题求解的实验结果表明，优化的tmd结果更优，算法的运行速度更快，耗时更短。将该方法应用智慧钻井过程的井眼轨迹优化，可增加优化过程实时性，降低钻井成本。

附图说明

图1是复杂井眼轨迹的垂直横截面。

图2是井眼轨迹中增斜段的三维示意图。

图3是本发明中(x,fn/fn+x)及其拟合关系式。

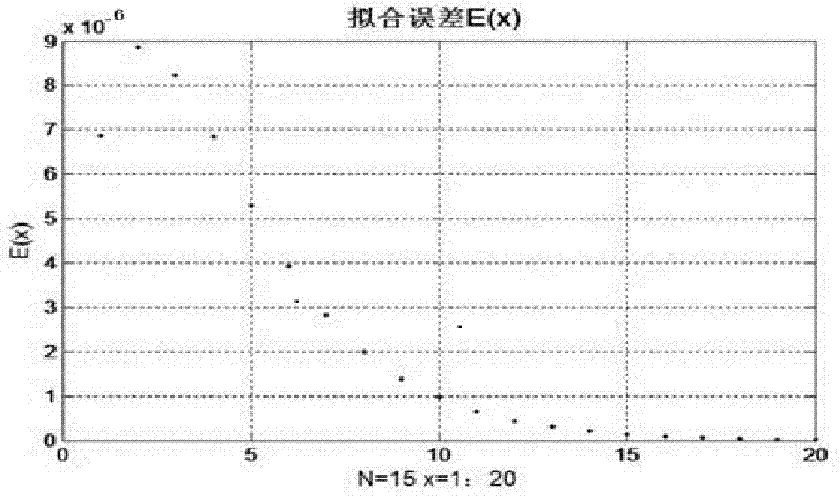
图4是拟合误差e(x)与x取值之间的关系。

图5是本发明采用faqga实现tmd优化的仿真结果。

图6是本发明采用faqga实现tvd优化的仿真结果。

具体实施方式

下面结合附图详细说明本发明的实施方式。

基于快速自适应量子遗传算法的复杂井眼轨迹优化方法，包括如下步骤：

(1)分析fibonacci数列特性，生成fibonacci数列，计算fn/fn+x。

①若用fn表示数列中的第n个元素，则fibonacci数列满足：

式(19)中，该数列从第三项开始，每一项都等于前两项之和。分析该数列，则有：

对式(20)两边取自然对数，则有：

ln(g(x))＝-x*ln(1.6180340)＝-0.4812x

(21)

式(21)中，x＝0,1,2......。当x＝0,1,2...,15，n＝15时，分析x和fn/fn+x拟合关系，其拟合关系式如图3所示，其中“*”表示表达式fn/fn+x的值，“+”表示表达式0.618^x的值，“—”线条为拟合关系曲线e^-0.4812x。

②量子旋转门的转角调整策略

分析量子旋转门的转角调整策略可知：在量子遗传算法的最优解搜索过程中，当搜索点处目标函数变化率较大时，能够适当的减小转角步长，阻止越过全局最优解，防止算法的振荡。反之，当搜索点处的目标适应度函数相对变化率较小时，适当的增加转角步长，以提高算法的收敛速度和鲁棒性。

图3中，若采用x反映搜索点处相邻两代目标函数变化值。当n＝15，x＝0,1,2…,15时，fn/fn+x与x之间的呈负指数关系正好符合量子旋转门的转角的调整策略。其关系式可表达为：

③误差分析

令拟合误差为e(x)＝e^-0.4812x-fn/fn+x，其中，n＝15且x∈[1,20],x∈n⁺。则e(x)与x的关系如图4所示。

观察图4可知，当n＝15且x∈[1,20],x∈n⁺时，误差e<9×10^-6；当n＝15且x∈[15,20],x∈n⁺时，误差几乎为零。

(2)初始化种群q(t)和设置算法参数。令iteration＝0，随机产生n条染色体组成初始化群体q0(t)；设置faqga的参数，如表1所示。随机生成的初始化种群θ和采用公式(26)生成在bloch球坐标体系下的量子染色体初始化种群。在约束条件及自变量约束边界条件如表1所示。

表1faqga的参数设置

表1是本发明实施后优选井眼轨迹参数与其他智能算法的比较；表1中，size为种群的规模，一般size取值为50～80，coder为链条的编码，对于faqga，coder为待优化的自变量的个数，在三维井眼轨迹优化问题中，codel＝16；gen_max为最大迭代次数；pm为变异概率；为单位转角步长。faqga转角θ和规模均为size*codel，解空间规模为size*codel*3。

在基于bloch球面坐标的量子遗传算法中，量子比特可表示为对于种群其中表示第t代的一条染色体，基于bloch球面坐标的量子染色体编码为：

式(23)θij＝π×rand。rand为(0,1)之间的随机数。i＝1,2,...,n，j＝1,2,...,m，n为种群规模，m为量子位个数。

(3)解空间变换。当优化过程限定在单位空间iⁿ＝[-1,1]ⁿ内，在bloch球面坐标中m个量子位有3m个坐标，利用线性变换，将这3m个坐标由n维单位空间iⁿ＝[-1,1]ⁿ映射优化问题的解空间，每个坐标对应解空间中的一个优化变量。第i条染色体所对应第j个量子位相应的解空间变量为：

式(24)中，和是量子位的bloch坐标值。每条染色体对应优化问题的三个解。bi和ai为优化问题解空间的最大值和最小值。由式(24)可将单位的空间iⁿ＝[-1,1]ⁿ映射到优化问题的解空间，得到近似解集x(t)，该解集的规模为50*16*3；因而，引入bloch球面坐标体系转换解空间，增加了解空间的遍历性。

(4)计算目标函数值。针对复杂井眼轨迹优化问题，本发明选择井身实际测量深度tmd(truemeasurementdepth，tmd)为优化目标，对井身、井斜角、井斜方位角以及井段曲率参数优选，以自变量的取值，套管的长度及目标垂直井深为约束条件，目标函数可定义为：

obj_function＝min{tmd}

其中：tmd＝dkop+d1+d2+d3+d4+d5+hd

s.t.xmin≤x≤xmax

casjmin≤casj≤casjmax

tvdmin≤tvd≤tvdmax(4)

式中，x＝(hd,phi1～phi3,theta1～theta6,dd,db,ds1～ds3,dkop)∈r¹⁶，解空间r¹⁶由16维决策向量x组成；即16为待优选参数的个数；tmd为优化目标函数，ft；j为套管设计的段数。其中，d1：firstbuild-upsection一段造斜段；d2：tangentsection正切段d3：drop-off降斜段；d4：holdsection稳斜段；d5：secondbuild-upsection第二段增斜段；hd：horizontalsection水平段。图1中，j＝1,2,3；tvdmin，tvdmax分别为井眼轨迹的垂深下限和上限。

其中，待优化复杂井眼轨迹的垂直横截面如图1所示。图1中，各段计算公式定义为：

d2＝(dd-dkop-d1×(sinφ1-sinφ0)/(φ1-φ0))/cos(φ1)

(6)

d4＝(db-dd-d3×(sinφ2-sinφ1)/(φ2-φ1))/cos(φ2)

(8)

其中d1，d5增斜段的三维示意图如图2所示。对于d1，d5增斜段曲线的曲率常数：

根据增斜段曲线长度为：

得到d1，d5增斜段曲线的曲率常数：

曲率半径：

图2中，增斜段曲线长度：

式(10)曲线段在三维坐标下的增量为：

式(4)～(14)中，各参数的含义及取值范围如表2所示。表2是本发明中faqga算法的复杂度与其他智能算法的比较；由式(4)～(14)计算目标函数tmd，并保存符合约束条件的最优解，将第一代最优解、最优染色体和最优目标函数值暂存，作为全局最优最优解global_xb、全局最有染色体和全局目标函数global_tmd。随着迭代次数的增加，根据式(4)计算目标适应度值tmd(gxb)，记录当代最优解gxb及其最优染色体在符合约束条件下，若tmd(gxb)<tmd(global_xb)，则否则，保持global_qb不变。令iteration＝iteration+1；

表2井眼轨迹变量约束边界及约束条件

(5)计算相邻两代目标函数的相对变化率x。在最优解的搜索过程中，考虑目标函数在搜索点的变化率，建立反映搜索点处的相邻两代目标适应度值相对变化值，记作x。并将该值引入到量子旋转门转角步长的更新策略中，以自适应调整算法的搜索方向和收敛速度，提高算法的运行效率。x可定义为：

式中，int(.)表示取整运算。x为size行coder列的步长调整矩阵，为目标函数f(x)在点梯度，和分别为相邻两代目标函数值梯度的最大、最小值，其定义为：

式(24)中，和分别表示父代和子代染色体。和分别表示父代和子代第*个染色体的第j个量子位的目标函数值。

(6)量子门的更新。在bloch球面坐标中，量子旋转门更新过程为：

式(16)中，u为酉矩阵。u的作用是使量子位的相位在xoy平面旋转和延z轴方向旋转δθ。转角步长和δθ的可定义为：

式(17)中，δφ0和δθ0为单位转角步长，δφ0＝δθ0＝0.05π；求符号函数sgn(a)中a及sgn(b)中b分别定义为：

式(25)中，当前最优染色体中的第j个量子位的bloch坐标为当代种群中第i条染色体的第j个量子位的bloch坐标为(其中：i＝1,2,...,n，j＝1,2,...,m)。确定和δθ方向的规则为：当a≠0时，方向为当a＝0时，方向取正、负均可；确定δθ方向的规则为：当b≠0时，方向为sgn(δθ)＝-sgn(b)；当b＝0时，方向取正、负均可。

(7)量子位的变异。在基于bloch球面坐标中，以变异概率为pm随机对若干个量子位执行h逻辑门变异操作，执行过程为：

式(18)实现量子位变异实质是对这若干个量子位的幅角同时逆时针旋转π/4，以保持种群的多样性，降低早熟收敛的概率。

(8)判断是否已达到最大迭代次数限制，即iteration<gen_max？若是，则转至(3)；否则，转至(9)；

(9)输出全局最优解global_xb，即输出global_xb＝(hd,phi1～phi3,theta1～theta6,dd,db,ds1～ds3,dkop)；输出全局最有染色体和全局目标函数global_tmd。采用faqga实现复杂井眼轨迹优化的结果与其他几种智能优化算法优化结果相比较，如表3所示。采用faqga优化tmd的仿真结果及tvd的优选结果如图5、图6所示。

表3采用faqga优化井眼轨迹优化结果与其他几种算法优化结果比较

由表3可知，在复杂三维井眼轨迹优化中，采用faqga实现tmd优化，其优化结果为14,807.5ft；算法的运行时间为3.5075s。与npso(aminatashnezhad2014)，ga(shokiretal.al.2004)，hcso(davida.wood，2016)，hbfo(davida.wood，2016)和pso(shokiretal.2004)算法优化结果相比较，最优解更优且算法的运行效率大幅提高，运行时间明显缩短。

对tsp问题，假设进化代数为t，若种群的规模为n，种群个体的自变量为k，m为粒子数，j为个体自变量染色体的编码长度，faqga与其他智能算法的时间复杂度与空间复杂度比较如表4所示。

1)时间复杂度

pso算法时间复杂度t(n)＝o(n²+m)，记作o(n²)；qga的时间复杂度t(n)＝o(eⁿ)，记作o(cⁿ)；而faqga算法时间复杂度t(n)＝o(n)，记作o(1)。ga算法时间复杂度t(n)＝o(n²)。

2)空间复杂度

pso算法的空间复杂度s(n)＝o(n²)+o(nm)；qga的空间复杂度s(n)＝o(nkj)，记作o(n³)，faqga的空间复杂度s(n)＝o(3nk)，记作o(n²)；ga的空间复杂度s(n)＝o(nkj)，记作o(n³)。

表4算法的时间复杂度和空间复杂度的比较

由表4可知，与pso，qga和ga算法比较，faqga在不增加算法空间复杂度的条件下，通过引入fibonacci数列，大大降低了算法的时间复杂度，因而提高算法的运行效率，缩短了运行时间。

从本发明的实施效果可知，由于将fibonacci数列的负指数特性，即g(x)＝(fn/fn+x)|n＝15≈e^-0.4812x特性引入到量子遗传算法转角步长和δθ的更新策略中，在保持算法空间复杂度o(n²)不变的情况下，将算法的时间复杂度降低为o(1)。由faqga实现复杂井眼轨迹优化结果看，该算法在优选的最优解和运行时间上，明显的优于其他智能算法。faqga充分的利用了qga算法超高速、超并行、全局搜索能力强等优点，通过映射到bloch球面坐标体系，增加解的遍历性。将faqga用于复杂三维井眼轨迹的实际测量深度tmd的优化，以多靶点的井眼轨迹为研究对象，完成井身、井斜角、井斜方位角以及井段曲率参数的优选，从而完成复杂三维井眼轨迹的设计。采用faqga实现复杂三维井眼轨迹tmd的优化，由图5可知，当iteration>145，tmd趋近于最优解1.48e+004ft。采用faqga实现复杂三维井眼轨迹垂直井深的优选。由图6可知，随着迭代次数增加，以及搜索到的最优tmd减小和种群中自变量的取值不同，tvd出现了波动，当iteration>145，tmd最优解趋于稳定，tvd趋于最优垂直井深1.0887e+004ft。采用faqga实现复杂井眼轨迹优化问题求解的实验结果表明：faqga优化的tmd结果更优，算法的运行速度更快，耗时更短。将该方法实际钻井过程中井眼轨迹优化，可增加优化过程实时性，提高钻井效率和成功率，降低钻井时间和节约钻井成本。

本发明针对在复杂三维井眼轨迹优化问题中自变量多，约束条件复杂的特点，为提高多靶点多井段复杂井眼轨迹优化结果的精度和优化速度，克服现有算法的实时较差的问题，本发明中设计了一种新的快速自适应量子遗传算法faqga(fastadjustmentquantumgeneticalgorithm，faqga)。该算法在bloch球面坐标体系下，引入fibonacci数列实现快速自适应调整的量子旋转门转角步长，利用量子遗传算法的超高速、超并行和全局寻优的特点，完成多靶点复杂三维井眼轨迹优化。首先，通过分析fibonacci数列，发现该数列具有负指数特性，将该特性引入到量子旋转门转角步长的更新策略中，在不增加算法的空间复杂度的同时降低算法的时间复杂度，大幅提高了算法的效率，缩短算法的运行时间。其次，将任意一个量子位与bloch球面上的点一一对应，从而增加解得遍历性。最后，针对多靶点复杂三维井眼轨迹优化问题，在各井段、套管长度及目标垂直井深约束条件下，应用faqga优化实际测量井深tmd(truemeasurementdepth，tmd)，完成井身、井斜角、井斜方位角以及井段曲率参数的优选，实现精确、高效的井眼轨迹优化。用faqga实现复杂井眼轨迹优化问题求解的实验结果表明：faqga优化的tmd结果更优，算法的运行速度更快，耗时更短。将该方法应用于实际钻井过程中井眼轨迹优化，可增加优化过程实时性，提高钻井效率和成功率，降低钻井时间，将节约钻井成本约1.46～4.64％。