一种基于模型压缩的递归神经网络加速器的硬件架构的制作方法

本发明涉及计算机及电子信息技术领域，特别是一种基于模型压缩的递归神经网络加速器的硬件架构。

背景技术：

递归神经网络有着强大的非线性拟合能力，其天然的递归结构十分适用于建模序列数据，如文本、语音和视频等。目前，递归神经网络模型在自然语言处理领域，尤其是在语音识别和机器翻译上已经取得了接近甚至超过人类的效果或准确率；通过结合增强学习，递归神经网络在机器人自适应控制和学习领域也有广泛的应用前景。这些技术是实现智能人机交互所必须的，但是在嵌入式设备上运行递归神经网络模型存在着诸多问题。一方面，递归神经网络模型需要存储大量的参数，而且计算量巨大；另一方面，嵌入式系统所能提供的存储资源和计算能力十分有限，无法满足模型存储和计算的需求，实时性和功耗上也面临着诸多挑战。由前者催生出一些模型压缩技术来减少网络模型的参数以减少模型的存储需求，并降低模型的计算复杂度。但是，现有的解决方案多采用gpu芯片，过高的功耗使之无法应用于嵌入式场景；而目前嵌入式系统中广泛采用的硬件平台无法很好地利用前述模型压缩技术。因此有必要设计专门的硬件架构以充分利用已有模型压缩技术。

现有的模型压缩技术可以粗略归为两大类，一类不减少模型参数个数，但可以减少参数存储所需要的空间。如通过剪枝使参数矩阵变稀疏，而后可通过特殊的格式存储稀疏参数矩阵；也可采用不同的参数量化方法，减少存储每个参数需要的比特。另一类是通过对参数矩阵施加特殊的约束减少参数个数或是减少计算复杂度，如通过哈希映射将网络参数限制为几种特殊的值，存储时存储值及每个参数所属的类别；或是将参数矩阵限制为一些结构化矩阵，如托普利兹矩阵或循环矩阵，不但可以减少存储空间，也可以通过快速算法减少计算的时间复杂度。

混合量化和结构化矩阵约束(尤其是循环矩阵约束)是十分高效的两种模型压缩技术，但目前已有的基于模型压缩的硬件架构多使用单一量化方式，且未考虑结构化矩阵约束带来的优势，因而还未很好地利用这两种技术，其在嵌入式场景下巨大的优势和潜力尚待发掘。

技术实现要素：

发明目的：

本发明所要解决的技术问题是针对递归神经网络无法满足嵌入式系统低功耗、低延迟的需求，提出一种基于模型压缩的递归神经网络加速器的硬件架构，使递归神经网络在低功耗、实时嵌入式系统上的应用成为可能。

技术方案：

为了解决上述技术问题，本发明公开了一种基于模型压缩的递归神经网络加速器的硬件架构，其特征在于，包括以下部分：

1、矩阵乘加单元mat-vec，用于实现神经网络中主要的矩阵向量乘法运算，该单元内含多个乘加单元簇mvu/cmvu，每个乘加单元簇用于处理递归神经网络中的一个矩阵向量乘法。

2、多个硬件友好的非线性计算单元sigmoid/tanh，用于实现神经网络中的非线性函数。

3、多个双端片上静态随机存储器，其中有两个存储中间状态的存储器hram0和hram1组成乒乓存储结构以提高数据存取效率，其余还包括另外一个状态存储器cram和由多个参数存储单元组成的参数存储单元块wrams用于存储递归神经网络的模型参数。

4、控制单元，用于产生相关控制信号及控制数据流的流动。

其中，乘加单元簇mvu/cmvu是本硬件架构的主要计算单元，每个乘加单元簇包含多个乘加单元块b-pe，而每个乘加单元块内又包含多个基本乘加单元pe。基本乘加单元用于实现多个数之间的基本乘加运算，不同的量化方法对应于不同的基本乘加单元结构。不同基本乘加单元的输出在乘加单元块内求和作为乘加单元块的输出，多个基本乘加单元的求和可以根据需要插入流水线以减少时序延迟，提高系统吞吐率。

对于循环矩阵向量乘法，通过一种针对硬件优化了的循环矩阵向量乘法重组方法，使其可以与普通的矩阵向量乘法共享相同的硬件架构，唯一的不同在于每个乘加单元簇中需额外包含与乘加单元块个数相同的移位单元用于实现额外的移位操作。为了区分该类乘加单元簇与普通乘加单元簇，将用于实现循环矩阵向量乘法的乘加单元簇定义为cmvu，而普通乘加单元簇定义为mvu。

整个递归神经网络加速器的并行度由上述乘加单元簇、乘加单元块和基本乘加单元的个数共同决定。

有益效果：

本发明所述硬件架构在底层支持不同的参数量化方法，在上层支持普通矩阵和循环矩阵两种类型的矩阵向量乘法运算，因而可以很好地利用模型压缩带来的算法上的优势，只需较少的存储空间和计算复杂度就可以获得较好的性能，硬件效率高；另一方面，本发明所述硬件架构有着十分简洁而统一的结构单元，支持配置成不同的并行度，可扩展性强，也可以在较低功耗下实现较高的吞吐率，适用于低功耗、实时嵌入式系统，是一种可用于智能人机交互、机器人控制等相关领域嵌入式系统的合理方案。

附图说明

下面结合附图和具体实施方式对本发明做更进一步的具体说明，本发明的上述和/或其他方面的优点将会变得更加清楚。

图1是本发明的顶层硬件架构图。

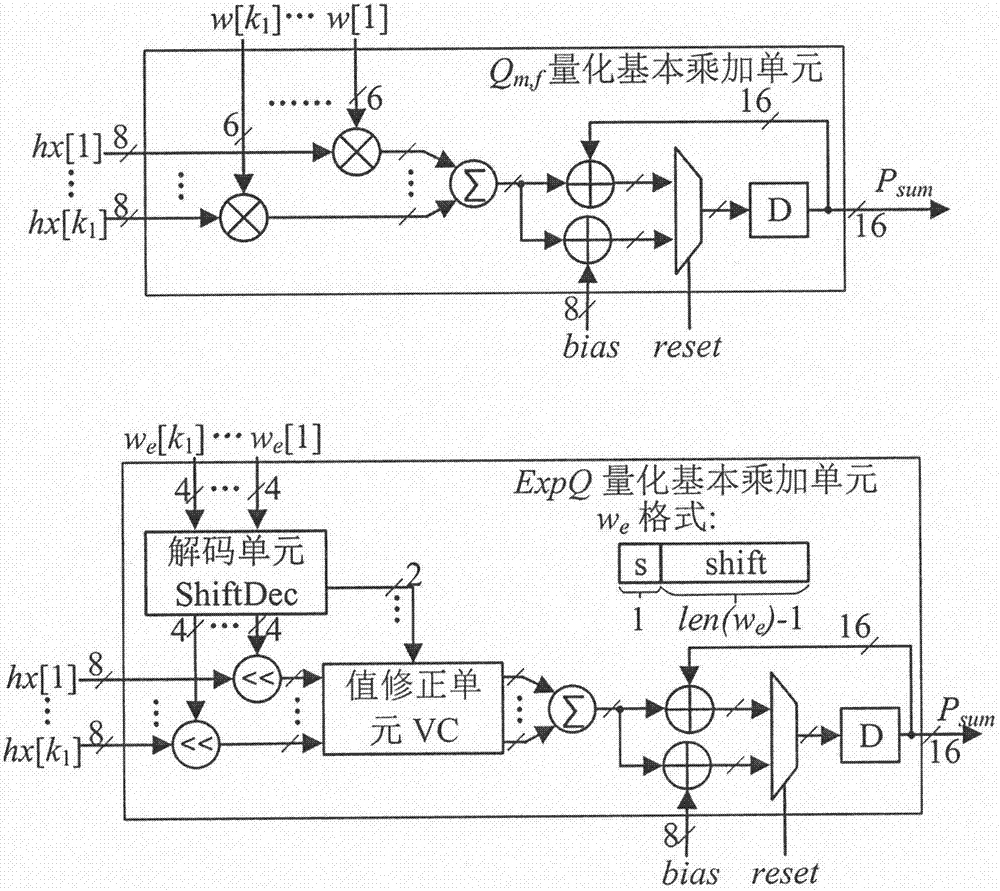
图2是两种不同量化方法下的基本乘加单元硬件架构图。

图3是乘加单元块的内部结构图。

图4是矩阵向量乘法所用棋盘分解方式说明图。

具体实施方式：

下面详细描述本发明的实施例。本实施例中将包含多个硬件单元输入输出变量的定义和说明，以及为了说明某一功能而引证的具体示例，旨在用于解释本发明，而不能理解为对本发明的限制。因递归神经网络包含多种变体，本实施例将不限制具体的递归神经网络变体类型，只讨论通用情况。

拥有n个输入和输出节点的递归神经网络的基本单元可定义为：

ht＝f(wxt+uht-1+b)，(1)

其中，ht∈r^n×1为t时刻递归神经网络的隐状态(中间状态)，同时也作为t时刻的输出；xt∈r^n×1为t时刻的输入向量；w、u∈r^n×n、b∈r^n×1为递归神经网络的模型参数，b为偏置项，w和u为参数矩阵；f为非线性函数，常见的有σ和tanh：

如公式1所示，每个递归神经网络的基本单元共有两个矩阵向量乘法和一个非线性函数。递归神经网络往往由一个至多个类似的基本单元组成。一次性计算所有的矩阵向量乘法对于存储资源和计算能力受限的嵌入式系统而言是不现实的，因此有必要将其分解成多个子计算过程。本实施例采用如图4所示的棋盘划分方法，将整个n×n矩阵乘以n×1向量的计算过程分解成p²个矩阵乘以向量的子过程。下面结合图1描述公式(1)所定义基本单元在本发明所述硬件架构下的计算流程：

对于每个时刻的输入，控制单元将依据图4所示棋盘划分方式，每次从存储单元wrams和hram0/hram1中读取相应的参数和中间状态到矩阵乘加单元mat-vec中，并按照图4所示从左至右，从上至下的顺序完成子矩阵向量乘法，计算结果保存在mat-vec中进行累加；当整行的p个子矩阵向量乘法完成之后，对应结果将输出至非线性计算单元完成非线性计算，进行状态更新后将更新后的状态存至状态存储单元，同时mat-vec单元清零进行下一行的子矩阵向量乘法计算，依次类推直至整个计算过程完成。

从公式(1)可以看到，t时刻的状态向量ht中每个元素的更新要取决于整个t-1时刻的状态向量ht-1，根据图4所示棋盘划分方式，每次整个模块只更新部分结果，直接将更新后的部分结果存回原存储地址将覆盖上一时刻的状态导致后续计算出错。为了解决这一问题，可以引入乒乓存储结构。如图1所示，维持两个大小相同的存储单元hram0和hram1，每个时刻从其中一个存储单元读取上一时刻的状态，更新后的状态存储于另外一个存储单元中，从而解决上述问题，同时提高数据存储效率。

如果在mat-vec单元中使用两个乘加单元簇，每个乘加单元簇处理公式(1)中的一个矩阵向量乘法，则整个更新过程共需要p²个时钟周期。

mat-vec是本发明所述硬件架构的主要单元，下面将从最基本的单元开始介绍其功能和实现细节：

1、基本乘加单元pe为模块的基本单元，用于实现多个数的乘加运算。对于不同的参数量化方式，其结构会有所不同。表格1给出了两种优选的量化方法，其中m为待量化的参数，表格右侧数学定义中的操作均为原子级操作，即若m为矩阵，则m＞0.5表示对矩阵中每个元素的大小与0.5进行比较。round函数表示将元素裁为与之最接近的整数，sign为符号函数，用于析离元素的正负号。对于表1中量种量化方式，expq将参数取值范围限制为2的倍数，因而参数的乘法可以用移位操作实现；qm，f为常见的量化方式，将参数量化成m位整数、f位小数外加一位符号位表示的形式。

表格1

对应于表1所述量化方式，图2给出了对应pe单元的硬件架构，可以实现k1个数的乘加运算，k1的大小可以根据实际情况进行选择。图2中带下标e的变量表示该变量使用expq量化方式，否则为qm，f量化方式。每个pe单元可实现以下功能：

对于expq量化方式，乘法可以使用移位实现，大大减少了所需硬件资源；在对参数进行存储时亦可考虑更叫高效的存储方式。本实施例优选地给出一种存储格式，参数根据图2表示为we，并设len为参数的量化宽度，第i位为we，i，we，i，j(j＜i)表示we的第j位到第i位，则其格式可以表示为：最高位为符号位，其符号表示为s(we)；其余len-1位表示we的指数项；因为当we为0时指数项无法用有限位数表示，在本实施例中规定当we指数项的大小为-2^len-1时we为0。

根据以上存储格式的定义，公式(3)中基本的运算w[i]·hx[i]可表示为：

如图2所示expq量化基本乘加单元，使用expq量化的参数在输入pe单元后先经过解码单元shiftdec分离出符号位和指数项，并判断对应数是否为0；指数项被输出与其他输入进行乘加(实际为移位)操作，而判断后的符号位和标志是否为0的标志位将被输入值修正单元vc以修正乘加后的值，得到准确结果。

2、如图3所示乘加单元块b-pe含k2个pe单元，可以认为是粗粒度版本的pe。每个pe单元的输出在b-pe单元内进一步的求和，该求和中间可以根据需要插入流水线以减少时延，插入位置在图3中用虚线加以标识。

3、乘加单元簇mvu/cmvu内含多个b-pe单元。根据前述介绍，每个mvu/cmvu每次处理一个的矩阵乘以的向量。假设mvu/cmvu中含r个b-pe单元，则r应满足

对于循环矩阵的情况，考虑y＝wh，其中为循环矩阵，对应的元向量w＝(w1，w2，…，wn)^t，则：

由公式(5)可以看出，直接对其使用，图4所示棋盘分解方式十分低效，无法很好地利用循环矩阵约束带来的优势。为此，我们考虑对公式(5)进行重组使其适用于棋盘分解的方式。优选地，我们考虑可以将元向量w根据前述相关参数的定义分解为p个子元向量：

wⁱ＝(wi，wi+p，wi+2p，…，wi+(r-1)p)，i＝1，2，…，p(6)

每个子元向量wⁱ对应于一个子循环矩阵wⁱ：

相应地，将向量h也按照类似w的方式分解：

hⁱ＝(hi，hi+p，hi+2p，…，hi+(r-1)p)，i＝1，2，…，p(8)

另外再定义大小一个r×r的辅助矩阵sr：

结合以上定义，原始公式(5)可以等价为：

可以看出，对公式(5)进行重组后得到的公式(10)满足图4所示棋盘划分方式。对于带循环矩阵约束的矩阵，乘加单元簇在处理子矩阵向量乘法时，每次只需根据当前处理的行列位置读取相应的子元向量并判断对应的子循环矩阵是否需要额外乘以sr即可。对某一子循环矩阵左乘sr等价于对该子循环矩阵做一次额外的行循环位移操作，而子循环矩阵的每一行都是上一行的循环右移。因此，相对于mvu单元，cmvu单元内需包含额外的位移单元来实现相应的功能。

整个计算流程由控制单元进行控制，用于给出复位或清零信号，指示当前正在处理的子矩阵向量乘法位置等。非线性计算单元sigmoid/tanh用于实现公式(2)中的非线性函数，在硬件上可以通过查找表实现，也可通过分段函数近似后使用纯组合逻辑实现，其实现方式并不唯一。

通过本发明实施例的上述硬件架构，扩展性强，可以在较低功耗下实现较高的吞吐率。而硬件架构中的主要单元mat-vec和其内部组成部件mvu/cmvu、b-pe、pe等均给出了功能说明，具体实现这些部分的功能的方法和途径很多。应当指出，对于本技术领域的普通技术人员来说，在不脱离本发明原理的前提下，还可以作出若干改进和润饰，这些改进和润饰也应视为本发明的保护范围。本实施例中未明确的各组成部分均可用现有技术加以实现。