一种基于闭环仿真的运载器分布载荷优化设计方法与流程

本发明涉及一种基于闭环仿真的运载器分布载荷优化设计方法，属于运载器总体设计领域。

背景技术：

传统的运载器分布载荷计算包括：气动载荷、操纵载荷、晃动载荷和弹性载荷等，其中气动载荷和操纵载荷是载荷专业依据姿控专业提供的攻摆角静态计算结果所计算得出的，由于未考虑控制系统间各个参数的相互影响，可以称之为开环载荷计算。首先，由于静态计算提供的攻摆角具有一定的保守性，相应的开环载荷在气动载荷和操纵载荷这两部分具有一定的保守性；其次，由于静态计算的限制，不能考虑摆动惯性力、气动阻尼力等产生的附加载荷，在进行晃动载荷和弹性载荷的计算中无法充分考虑控制的加入对这两部分载荷的影响；再次，开环载荷计算是基于人为确定的某些特征工况开展的，不能覆盖火箭飞行过程中的所有工况；其中晃动载荷和弹性载荷的计算流程类似，晃动尾翼和弹性位移均为根据经验自行取值，设计余量往往较大。

因此，开环载荷计算一方面具有一定的保守性，另一方面也不够全面完整，非常有必要开展基于火箭六自由度全量动力学闭环仿真下的运载器分布载荷优化技术研究，即闭环载荷计算。

技术实现要素：

本发明的技术解决问题是：克服现有技术的不足，提供一种基于闭环仿真的运载器分布载荷优化设计方法，能够真实反映火箭在飞行过程中的运载器各个部段所受的载荷，对复核载荷设计的完备性和设计余量具有重大意义。

本发明的技术解决方案是：一种基于闭环仿真的运载器分布载荷优化设计方法，包括以下步骤：

(1)为运载器建立六自由度动力学模型；

(2)利用六自由度动力学模型进行闭环仿真，得到发动机推力、气动力、控制摆角、飞行攻角、运载器绕心角加速度、压心位置、质心位置、运载器质心加速度；

(3)建立运载器分布载荷剪力计算模型，结合步骤(2)得到的动力学参数计算运载器每个站点下截面剪力；

(4)建立运载器分布载荷弯矩计算模型，结合步骤(2)得到的动力学参数计算运载器每个站点下截面弯矩；

(5)建立运载器分布载荷轴力计算模型，结合步骤(2)得到的动力学参数计算运载器每个站点截面轴力；

(6)基于步骤(3)-(5)的计算结果，并复核运载器载荷满足情况，若满足则设计结束，若不满足则优化步骤(2)的仿真输入，重新获得动力学参数，重复步骤(3)-(5)，直到运载器载荷满足要求。

所述步骤(3)中建立运载器分布载荷剪力计算模型的过程如下：

设运载器分站站号为i＝1～s，站点距理论尖点距离为xi，站点质量为mi；分支梁站号为fi＝1～l，分支梁与运载器对接处距理论尖点距离为xfi，分支梁质心距理论尖点距离为xfti，站点质量为mfi；运载器受到集中力为1～k，其中第j个集中力大小为fj，集中力作用位置距离理论尖点的距离为xfj；

以1～n个站点整体做力平衡分析得到第n个站点下截面剪力计算公式如下：

其中力的方向以运载器体坐标系+y1轴方向为正；

qn为第n个站点的下截面剪力；

δ(xn-xr)、δ(xn-xfj)为单位阶跃函数；

faj为第j站点所受到的气动力；

xz为运载器质心位置距离理论尖点的距离，xnz为1～n个站点的合质心距理论尖点的距离；

为运载器绕体坐标系+z1轴的角加速度，为运载器质心视加速度，α为飞行攻角，q为飞行动压，sm为运载器气动参考面积，为第j个站点的法向力系数导数；

xy为压心位置；

p、分别为发动机推力和控制摆角；

xr为发动机推力作用点距离理论尖点的距离。

所述步骤(4)中以1～n个站点整体做力矩平衡分析得到第n个站点弯矩计算模型如下：

其中，

jz为运载器绕体坐标系+z1的转动惯量。

所述步骤(4)中建立运载器分布载荷轴力计算模型的过程如下：

以运载器体坐标系+x1轴定义力的正方向，则运载器第n个站点所受到的轴力t(xn)计算模型为：

式中：

nx为飞行轴向过载，由六自由度动力学模型闭环计算得到；

mli为集中质量，xli为集中质量距离理论尖点的距离；

cxi为第i个站点的分布气动轴力系数；

px为发动机轴向推力；

nb为助推器个数，tb为助推器传递给芯级的轴向力合力，xb为助推器传力点距离理论尖点的距离。

所述tb满足：-tb+pzx-nxmzg-dzx＝0

式中pzx为助推器发动机轴向推力，dzx为助推器受到的气动轴力,mz为当前助推器总质量。

与现有技术相比，本发明具有如下有益效果：

本发明建立了运载器分布载荷剪力计算模型、弯矩计算模型、轴力计算模型，将上述计算模型与六自由度动力学仿真模型进行结合，每个模型的计算输入均为闭环仿真结果，从而保证载荷计算结果能够真实反映火箭在飞行过程中的运载器各个部段所受的载荷，对复核载荷设计的完备性和设计余量具有重大意义。

附图说明

图1为本发明流程图；

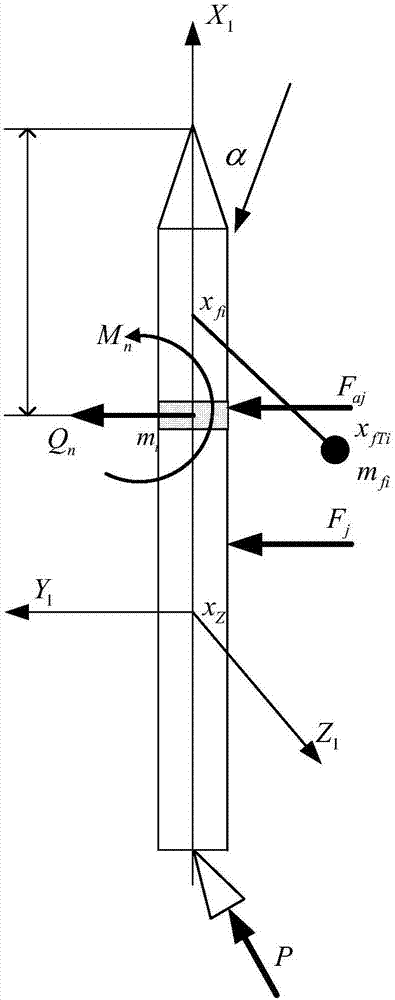
图2为运载器分布载荷剪力模型推导示意图；

图3为分布载荷轴力模型推导示意图；

图4为53s芯级轴力载荷计算结果与传统方法比对示意图。

具体实施方式

如图1所示，本发明的步骤如下：

(1)为运载器建立六自由度动力学模型。

建立过程如下：

首先按照如下方法建立质心动力学方程：

为运载器坐标系视加速度

为发射系到发惯系转换矩阵

v＝l^t(a0,b0,ωe,t)va-ωe×r

式中:

运载器质心在发射惯性系中的加速度；xa,ya,za：运载器质心在发射惯性坐标系中的位置

运载器质心相对于发射惯性坐标系的速度。

为箭体坐标系至发射惯性系之间的转换矩阵；γ,ψ,分别为滚动角、偏航角、俯仰角；

为箭体坐标系下视加速度；

gax,gay,gaz为发射坐标系下重力加速度；

a0：发射方位角；

b0：发射点的地理纬度；

ωe：地球自转角速度；

m：运载器质量；

faero、fp、分别为气动力、气动阻尼力、发动机推力、发动机摆动惯性力；

分别为液体推进剂晃动和运载器弹性对刚体作用。

然后按照如下过程建立绕心动力学方程：

式中：

转动惯量矩阵绕质心角速度斜对称矩阵其中分别为绕x1轴、y1轴、z1轴的转动惯量，为惯量积。

mp、maero、mslosh分别为发动机推力力矩、发动机摆动惯性力矩、气动力矩、气动阻尼力矩、液体推进剂晃动对运载器产生的作用力矩。

(2)利用六自由度动力学模型进行闭环仿真，得到发动机推力、气动力、控制摆角、飞行攻角、运载器绕心角加速度、压心位置、质心位置、运载器质心加速度。

(3)建立运载器分布载荷剪力计算模型，结合步骤(2)得到的动力学参数计算运载器每个站点下截面剪力。

如图2所示，设运载器分站站号为i＝1～s，站点距理论尖点距离为xi，站点质量为mi；分支梁站号为fi＝1～l，分支梁与运载器对接处距理论尖点距离为xfi，分支梁质心距理论尖点距离为xfti，站点质量为mfi；运载器受到集中力(晃动力、外力)为1～k，其中第j个集中力大小为fj，集中力作用位置距离理论尖点的距离为xfj；

以1～n个站点整体做力平衡分析得到第n个站点下截面剪力计算公式如下：

其中力的方向以运载器体坐标系+y1轴方向为正；

qn为第n个站点的下截面剪力；

δ(xn-xr)、δ(xn-xfj)为单位阶跃函数；

faj为第j站点所受到的气动力；

xz为运载器质心位置距离理论尖点的距离，xnz为1～n个站点的合质心距理论尖点的距离；

为运载器绕体坐标系+z1轴的角加速度，为运载器质心视加速度，α为飞行攻角，q为飞行动压，sm为运载器气动参考面积，为第j个站点的法向力系数导数；

xy为压心位置；

p、分别为发动机推力和控制摆角；

xr为发动机推力作用点距离理论尖点的距离。

(4)建立运载器分布载荷弯矩计算模型，结合步骤(2)得到的动力学参数计算运载器每个站点下截面弯矩。

以1～n个站点整体做力矩平衡分析得到第n个站点弯矩计算模型过程如下：

考虑以下求和变换公式：

将其代入弯矩方程中继续推导可得

进一步推导得到：

其中，

jz为运载器绕体坐标系+z1的转动惯量。

(5)建立运载器分布载荷轴力计算模型，结合步骤(2)得到的动力学参数计算运载器每个站点截面轴力。

如图3所示，以运载器体坐标系+x1轴定义力的正方向，则运载器第n个站点所受到的轴力t(xn)计算模型为：

式中：

nx为飞行轴向过载，由六自由度动力学模型闭环计算得到；

mli为集中质量，xli为集中质量距离理论尖点的距离；

cxi为第i个站点的分布气动轴力系数；

px为发动机轴向推力；

nb为助推器个数，tb为助推器传递给芯级的轴向力合力，xb为助推器传力点距离理论尖点的距离。

tb满足：-tb+pzx-nxmzg-dzx＝0

式中pzx为助推器发动机轴向推力，dzx为助推器受到的气动轴力,mz为当前助推器总质量。

(6)基于步骤(3)-(5)的计算结果，并复核运载器载荷满足情况，若满足则设计结束，若不满足则优化步骤(2)的仿真输入(通过分析飞行参数对运载器分布载荷的影响确定优化变量)，重新获得动力学参数，重复步骤(3)-(5)，直到运载器载荷满足要求。

本发明建立了六自由度动力学模型和分布载荷计算模型，考虑各项偏差和干扰，通过六自由度动力学模型闭环仿真得到运载器视加速度、绕心角加速度、过载、气动数据、动力数据等，输入给分布载荷计算模型，计算包括捆绑连接载荷在内的运载器各个质量站点所受到的载荷，实现与真实飞行状态更加匹配的运载器分布载荷计算，并最终达到复核、优化载荷设计结果的目的。本方法能量化分析各项因素对运载器分布载荷的影响，有利于提升载荷计算的精确性，能降低传统计算方法中的不确定性，进而提高运载载荷设计的精细化水平。

本发明方法能够真实反映火箭在飞行过程中的运载器各个部段所受的载荷，对复核载荷设计的完备性和设计余量具有重大意义。此外，本方法还能够验证主动减载方案对载荷分布的影响，是飞行中真实载荷的的有效评估手段。

本发明方法已应用于我国某助推捆绑构型火箭载荷设计工作中，53s芯级轴力载荷计算结果与传统方法比对如图4所示，图中横轴为运载器轴向位置，纵轴为载荷计算结果(归一化后)，比对不难看出基于闭环仿真的分布载荷计算结果要相比传统计算方法更为优化，传统方法设计结果更为保守。由于该方法的通用性，可推广应用于在飞型号的载荷复核以及未来型号的载荷优化设计中。

本发明说明书中未作详细描述的内容属本领域技术人员的公知技术。