脆性材料热破裂的数值模拟方法与流程

本发明涉及岩石力学与工程、采矿工程领域，具体涉及一种脆性材料热破裂的数值模拟方法。

背景技术：

热应力是引起岩石等脆性材料破坏的一个重要因素，当热应力超过材料自身的强度极限，就会使材料产生破裂。热破裂会对岩石的弹性和机械破裂性质造成很大的影响，并引起岩石物性参数(如孔隙度、渗透率等)的变化，从而对许多工程造成重大影响。例如：在核废料的存储中，由于核废料裂变而使围岩温度显著升高，导致岩石的热破裂，地下水的渗入会进一步加剧围岩破坏、甚至导致核素迁移，造成地下水污染；在石油开采中，利用岩石的热破裂，增加岩石的渗透性。目前，脆性材料热破裂的数值模拟研究方法主要有不连续变形分析法、有限元法、颗粒法等，这些方法普遍存在部分力学参数很难准确估算，无法对工程实际进行准确的模拟和仿真。

传统有限元方法模拟裂纹扩展时通常需要在裂尖构建奇异单元，且随着裂纹扩展不断地进行网格重构，该方法实现困难且低效。边界元法虽然避免了网格重新划分的问题，但严重依赖于问题的基本解，对于非线性、非均质等问题其优势大大降低。本发明的裂纹处理采用三角单元网格开裂技术，该技术只对裂尖局部单元进行网格调整，不涉及不连续位移场的处理问题，也无须引入额外自由度，更加简便、高效，具有较好的适用性。

技术实现要素：

针对现有技术中的上述不足，本发明旨在提供一种脆性材料热破裂的数值模拟方法，对脆性材料在热应力作用下产生的拉张破坏过程进行模拟，为分析脆性材料的热破坏过程和机制提供一种新的有限元方法。

为了达到上述发明目的，本发明采用的技术方案为：

提供一种脆性材料热破裂的数值模拟方法，其包括以下步骤，

采用工程对象数字模型对脆性材料进行计算网格划分；

设置模拟时的材料参数、温度边界、应力限定边界和位移限定边界；

计算应力场：

{σ}＝[d]([b]·{δ}^e-{ε0})

其中，[d]为弹性矩阵；[b]为应变矩阵；{ε0}为温度变化引起的变形；{δ}^e为单元位移；

当计算网格中存在一个节点的第一主应力大于等于脆性材料抗拉强度时，对该节点所在处的待开裂单元进行开裂处理得到新形成的计算网格，并返回计算应力场步骤；

当存在多个节点的第一主应力大于等于脆性材料抗拉强度时，对承受最大第一主应力的节点所在处的待开裂单元进行开裂处理得到新形成的计算网格，并返回计算应力场步骤；

当所有节点的第一主应力均小于脆性材料抗拉强度，且模拟时间未达到设置模拟时长时，按设定值递增温度边界后返回计算应力场步骤，否则停止模拟操作；

所述待开裂单元为包含第一主应力大于等于其抗拉强度的节点的单元、且位于裂纹扩展方向上的单元。

本发明的有益效果为：本方案能够通过设置的材料参数和各种边界条件模拟脆性材料由不同热膨胀系数产生的热应力破坏模式，并对遭到破坏的单元进行开裂处理，以降低热破裂对脆性材料的弹性和机械破裂性质造成的影响；采用该数值模拟方法能够准确反映出在温度荷载下，脆性材料拉张破坏过程，并能有效地分析裂纹开裂规律和应力转移变化过程。

本发明的裂纹处理过程中，裂纹可以直接劈开一个单元，或沿单元边界扩展，因此裂纹能够不受初始网格的限制沿任意路径扩展；与现有的网格重构算法相比，该方法只须对裂尖局部单元进行网格开裂或节点移动，更加简便、高效，具有较好的适用性。

附图说明

图1为脆性材料热破裂的数值模拟方法一个实施例的流程图。

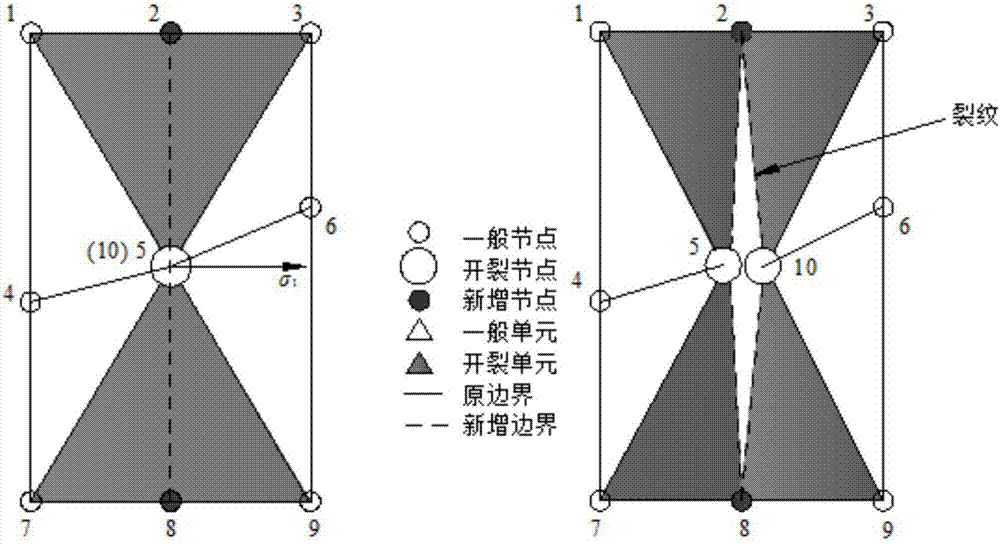
图2为脆性材料热破裂的数值模拟方法的三角形单元开裂示意图。

图3为脆性材料中内嵌颗粒圆形试样模型示意图。

图4a为t＝350℃时内嵌颗粒圆形试样第一主应力示意图。

图4b为t＝370℃时内嵌颗粒圆形试样第一主应力示意图。

图5为t＝390℃时内嵌颗粒圆形试样裂纹扩展过程和应力转移过程第一主应力示意图。

图6为t＝400℃时内嵌颗粒圆形试样裂纹扩展过程和应力转移过程第一主应力示意图。

图7为试样模拟结果与实验结果效果对比示意图。

具体实施方式

下面对本发明的具体实施方式进行描述，以便于本技术领域的技术人员理解本发明，但应该清楚，本发明不限于具体实施方式的范围，对本技术领域的普通技术人员来讲，只要各种变化在所附的权利要求限定和确定的本发明的精神和范围内，这些变化是显而易见的，一切利用本发明构思的发明创造均在保护之列。

参考图1，图1示意性地示出了脆性材料热破裂的数值模拟方法一个实施例的流程图；如图1所示，该方法包括步骤101至步骤106。

在步骤101中，采用工程对象数字模型对脆性材料进行计算网格划分；其中，模型中的网格被划分为三角形三节点单元。本方案中构建的模型是采用数值分析通用图形用户界面进行创建的。

在步骤102中，设置模拟时的材料参数、温度边界、应力限定边界和位移限定边界；其中的材料参数包括材料密度、弹性模量、泊松比、热膨胀系数、热传导系数和抗拉强度。

在步骤103中，计算应力场：

{σ}＝[d]([b]·{δ}^e-{ε0})

其中，[d]为弹性矩阵，其为由弹性模量e和泊松比ν控制的各向同性矩阵；[b]为应变矩阵；{ε0}为温度变化引起的变形；{δ}^e为单元位移。

由于应力场是基于温度场和位移场进行获得的，本方案在获得应力场之前还需要对温度场和位移场进行求解。

在本发明的一个实施例中，温度场的获取方法为：

温度场计算采用fourier导热定律：

其中，ρ为材料密度kg/m³；k为在x、y方向的热传导系数(w/m·℃)；c为比热值(j/m³·℃)；t为时间；t为温度(℃)。

由于本方案主要针对稳态热传导进行模拟，所以温度不随时间变化时，则kii▽²t＝0，此时，i＝1,2，将得到的热传导系数带入fourier导热定律公式，得到温度场t。

位移场的获取方法为，采用常规有限单元法求解位移场：

[k]·{δ}＝{q}t

其中，[k]为刚度矩阵，{q}t为热荷载(受热膨胀而形成的相当荷载)。

实施时，计算应力采用的由于温度变化引起的变形{ε0}的表达式为：

{ε0}＝αt[110]

其中，α为材料的热膨胀系数，t为温度的变化。

在步骤104中，当计算网格中存在一个节点的第一主应力大于等于脆性材料抗拉强度时，对该节点所在处的待开裂单元进行开裂处理得到新形成的计算网格，并返回计算应力场步骤。

在步骤105中，当存在多个节点的第一主应力大于等于脆性材料抗拉强度时，对承受最大第一主应力的节点所在处的待开裂单元进行开裂处理得到新形成的计算网格，并返回计算应力场步骤。

其中，待开裂单元为包含第一主应力大于等于其抗拉强度的节点的单元、且位于裂纹扩展方向上的单元。

本方案的待开裂单元是基于拉张破坏原理而确定的，其中拉张破坏原理为：当节点第一主应力大于等于岩石的抗拉强度时，岩石发生拉张破坏；如果有多个节点的第一主应力大于等于抗拉强度时，承受最大第一主应力的点破裂。

在本发明的一个实施例中，第一主应力的表达式为：

其中，σ1为第一主应力；σx为x轴方向上的应力；σy为y轴方向上的应力；τxy为y轴上切应力；

第一主应力与x轴间夹角为：

实施时，本方案优选对待开裂单元进行开裂处理进一步包括：获取裂纹扩展方向与待开裂单元的开裂边形成的交点；增加与第一主应力大于等于脆性材料抗拉强度的节点相重合的新增节点；根据新增节点和交点，将待开裂单元沿裂纹扩展方向裂开。

由于单元开裂后，可能引起部分单元几何性质不良，特别当裂纹扩展方向与单元边之间的夹角很小时，将会形成较差的计算网格。

实施时，本方案优选在新形成的计算网格与返回计算应力场步骤之间还包括对新形成的计算网格进行修正处理。采用修正处理后，能够保证计算网格计算的精度。

在本发明的一个实施例中，修正处理时的具体实现方法为：

当单元与裂纹扩展方向之间的夹角小于设定值时，判断单元短边与长边的比值是否小于设定最小比值(小于1的实值)：

若小于，则将计算网格的边移动至裂纹扩展方向，通过合并节点删除夹角小于设定值的单元。

在步骤106中，当所有节点的第一主应力均小于脆性材料抗拉强度，且未达到设置模拟时长时，按设定值(时间步)递增温度边界后返回计算应力场步骤，否则停止模拟操作。

为实现对开裂处理过程的数值模拟结果的处理，本方案根据时间步来自动保存数据文件，即每隔设定时间步长自动保存该时间步长内计算网格的单元数据，之后再为下一温度载荷计算做准备。

下面结合附图2详细描述三角形三节点单元的开裂过程：

①判断开裂单元。假如节点n5满足拉张破坏原理，查找包含节点n5的所有单元，在裂纹扩展方向上的单元即为需要开裂的单元，即单元e1-3-5和e7-5-9；

②增加交点。沿裂纹扩展方向找到需要开裂单元开裂边上的交点n2和n8；

③增加重合节点。增加与开裂节点n5重合的节点n10；

④劈开单元。根据新增节点(包括重合节点)，将单元沿裂纹扩展方向劈开，即开裂单元e1-3-5和e7-5-9会在新增加的节点n2，n8和n10的基础上劈开为四个独立的单元e1-2-5，e10-2-3和e7-5-8，e8-10-9；

⑤修正单元网格。非开裂单元e3-5-6，e9-5-6单元信息会在新增重合节点的基础上修改为e3-10-6，e9-10-6，单元e1-5-4和e7-5-4则保持不变。

下面结合具体的实例对本方案的数值模拟方法进行说明：

本实施例为一种由热膨胀系数不同所导致的材料破裂模式的数值模拟形式，其具体步骤为：

(1)建立工程对象数字模型，如图3所示，计算实例为带有颗粒的圆形试样，模型是由两个同心圆组成，内圆直径为12mm，外圆直径为25mm，内、外同心圆分别表示两种不同的材料，分别命名为颗粒和基质。

(2)施加材料参数，颗粒和基质的具体材料参数见表1；

表1材料力学参数

(3)设置时间控制步长，总时间t＝40s，时间步(每隔设定时间步长)δt＝1s；

(4)施加温度边界条件，实验设置模型基质和中央的颗粒施加相同的温度条件，初始温度t＝0℃，以δt＝10℃的温度增量不断升温。

(5)计算模型温度场、位移场和应力场，根据步骤(2)、步骤(3)所获取的材料参数和边界条件，通过有限元程序自动生成系统fepg计算模型的各个场值。

(6)计算第一主应力和方向角。将步骤(5)计算所得的应力值带入，进一步计算第一主应力及其方向角。

(7)判断是否有单元开裂。由强度准则判断是否有单元满足开裂条件，若有单元满足开裂条件，劈开单元(开裂流程详见图2)，重复步骤(5)～(7)；若没有单元满足开裂条件，保存当前时间步的开裂结果，并判断是否达到设置的总时间，若没有达到设置的总时间，增加温度增量δt，即温度tn+1＝tn+δt，重复步骤(4)～(7)；若达到设置的总时间，结束程序计算。

(8)查看厚壁圆筒试样在第一主应力场下的开裂结果。

图4a为t＝350℃时内嵌颗粒圆形试样第一主应力示意图。图4b为t＝370℃时内嵌颗粒圆形试样第一主应力示意图。图5为t＝390℃时内嵌颗粒圆形试样开裂过程第一主应力示意图。图6为t＝400℃时内嵌颗粒圆形试样开裂过程第一主应力示意图。

从这些视图可以看出，在升温过程中，由于基质和颗粒具有不同的热膨胀系数，造成了基质和颗粒的界面上变形的不协调，继而在颗粒周围产生了应力集中现象，升温的初始阶段，模型中应力处于积聚过程，但不满足开裂条件，未有破坏现象发生；t＝390℃时，试样基质中靠近颗粒的区域开始发生破坏，t＝400℃裂纹在原有的基础上进一步扩展，最终形成一条主裂纹将基质贯通破坏。

图7为试样模拟结果与实验结果对比图，由图7可以看出试样最终破坏模式与实验结果相符合。