一种多轴数控机床C轴几何误差测量系统及参数辨识方法与流程

本发明涉及一种几何误差参数辨识测量系统及方法，适用于多轴数控机床旋转轴c轴，通过建立理论数学模型与实际测量值的关系，实现几何误差参数的识别。

背景技术：

在现代制造业中，多轴数控机床能同时调整刀具相对于工件的切削位置和方向。因此，相对于传统的三轴数控加工，多轴数控机床具有更高的切削效率和加工精度，在航空、航天、能源和国防等领域中加工复杂零件起到一个重要的作用，是提升我国制造水平的技术突破口。

但由于多轴数控机床增加了旋转轴，其几何误差参数显著增多，且相互存在复杂耦合关系。因此给几何误差参数的辨识带来了较大的困难，同时对误差辨识方法提出了更高的要求，目前，针对旋转轴的辨识方法相对较少，且大多数对模型中的误差参数进行了简化，忽略了各个误差参数之间的耦合情况，导致辨识精度下降。因此探索一种较为准确的误差辨识方法，全面考虑误差参数的耦合关系，实现多轴数控机床几何误差参数的准确辨识是十分必要的。

鉴于多轴数控机床旋转轴的类似性，又由于c轴是多轴数控机床中一种比较常见的旋转轴，因此对于c轴的几何误差参数的辨识方法的研究具有一定的代表性。

技术实现要素：

针对多轴数控机床旋转轴辨识方法中存在的问题，本发明提出了一种基于多体系统理论的多轴数控机床c轴几何误差参数辨识方法，本发明避免了几何误差参数简化现象和参数间的耦合关系，在对平动轴的误差已经被补偿的基础上，认为平动轴的运动所形成的轨迹即为理想轨迹，采用多轴联动，利用多体系统理论，建立不同联动模式下有几何误差的运动方程，从而实现c轴几何误差参数的辨识。

一种基于多体系统理论的多轴数控机床c轴几何误差参数辨识方法，该方法包括以下步骤：

(1)建立相邻两体运动关系方程

如图1所示为两个运动体的相互位置情况，令{rl}＝{rxryrz1}^t表示l体上pl点相对于l体坐标系的位置阵列，令{plh}＝{xlhylhzlh1}^t表示pl点相对于i体坐标系的位置阵列，根据多体系统理论建立两体运动关系方程，由此可得：

{plh}＝[sil]p[sil]pe[sil]s[sil]se{rl}(1)

式中，[sil]p为l体相对于i体的相对位置变换矩阵，[sil]pe为l体相对于i体的相对位置误差变换矩阵，[sil]s为l体相对于i体的相对运动变换矩阵，[sil]se为l体相对于i体的相对运动误差变换矩阵。

(2)c轴几何误差参数辨识方法分析

c轴几何误差参数总共8项，分别为：与位置点有关的跳动误差(δx(c)，δy(c)，δz(c))、颠摆和偏摆误差(εx(c)，εy(c))、滚摆误差(εz(c))和与位置点无关的垂直度误差(εxc，εyc)。

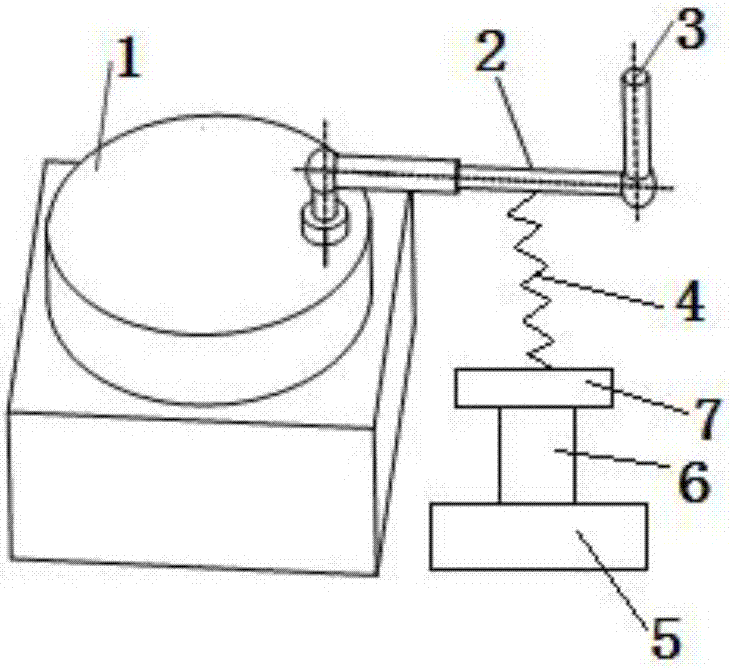
如图2所示，一种多轴数控机床c轴几何误差测量系统，该测量系统包括多轴数控机床c轴1、球杆仪2、刀具主轴3、弹簧4、移动配重块5、调节支撑杆6和底座7；多轴数控机床c轴1为工作台，球杆仪2的两端部分别连接多轴数控机床c轴1和刀具主轴3，球杆仪2的端部一连接在工作台的表面，端部一固定在工作台的偏心处；球杆仪2的端部二直接连接刀具主轴3，球杆仪2水平布置，刀具主轴3竖直布置；球杆仪2的中间段为伸缩杆，伸缩杆通过与弹簧4与移动配重块5连接，移动配重块5安装在调节支撑杆6上，调节支撑杆6固定在底座7上，弹簧4和移动配重块5组成球杆仪2的减振结构；移动配重块5的竖直方向位置由调节支撑杆6的伸缩长度控制。

多轴数控机床c轴1利用球杆仪2进行测量，测量时球杆仪2的一端固定在多轴数控机床c轴1另上设定的位置，一端固定在刀具主轴3上，预设定联动的轨迹，实现c轴转动的同时x轴、y轴同步联动，x轴、y轴为水平面上的水平向和竖直向，保证球杆仪2的两端同步运动，从而达到测量几何误差的目的。

如图3所示，ph点为球杆仪与工作台(c轴)连接端，ah、bh、dh点为与刀具主轴连接端，假设在运动时轴x轴、y轴误差均已被补偿，则ah、bh、dh点在运动过程中形成的轨迹为理想轨迹，由于运动时工作台(c轴)存在几何误差，因此工作台(c轴)上一点ph在实际运动过程中就会偏离理想位置ph点到达实际位置ph′点，phah、phbh、phdh分别是径向、切向、轴向测量的球杆仪理想位姿，且理论长度分别为dr、dt、ds，由于几何误差误差的存在，实际运动过程中phah、phbh、phdh变为了ph′ah、ph′bh、ph′dh。

ql-xqlyqlzql坐标系为l体实际运动参考坐标系，为l体实际体参考坐标系，ql-xqlyqlzql与之间的关系表明l体的运动情况，理想点ph、ah、bh、dh在坐标系ql-xqlyqlzql中的位置为：

(3)径向几何误差参数识别

如图3(b)所示，根据式(1)可得，在径向模式下理论位置点ph通过有误差的运动链描述到旋转中心处静止坐标系中，可得实际位置点ph′为：

式中，ch为工作台(c轴)旋转的角度，l为球杆仪工作台端球中心在旋转中心坐标系x向坐标值，h为球杆仪工作台端球中心在旋转中心坐标系z向坐标值。

由于与刀具主轴联接端的运动轨迹为理想轨迹，因此根据(1)式，将矩阵中运动误差参数均置为零，可得理论位置点ah在坐标系中的无运动误差的位置点为：

式中，dr为径向的球杆仪理论长度。

则在坐标系中，ph′与ah之差为：

根据式(4)求得ph′与ah之间的距离表达式为：

根据式(5)建立如下等式：

式中，δdr为球杆仪从初始位置到第h个位置的径向杆长变化量。

将(6)式方程两边同时平方化简可得：

-δx(ch)-h(εy(ch)+εxccosch-εycsinch)＝δdr(7)

在(7)式中，令：

wh＝εy(ch)+εxccosch-εycsinch(8)

取二组不同h的可以得到：

-δx(ch)-h1wh＝δdr1(9)

-δx(ch)-h2wh＝δdr2(10)

用式(10)减去式(9)可得：

将式(11)代入(9)可得：

δx(ch)＝-h1wh-δdr1(12)

当ch＝0即轴还未运动，运动角误差εy(ch)为0，由此可得：

εxc＝w0(13)

(4)切向几何误差参数识别

如图3(a)所示，同理可得，在坐标系中，ph′与bh之差为:

根据式(14)求得ph′与bh之间的距离表达式为：

根据式(15)建立等式:

式中，δdt为球杆仪从初始位置到第h个位置的切向杆长变化量。

对(16)式两边同时平方化简可得：

δy(ch)+lεz(ch)-h(εx(ch)+εxcsinch+εyccosch)＝δdt(17)

在式(17)中，令：

vh＝εx(ch)+εxcsinch+εyccosch(18)

取两组不同的h得到如下式：

δy(ch)+l1εz(ch)-h1vh＝δdt1(19)

δy(ch)+l1εz(ch)-h2vh＝δdt2(20)

用式(20)减去式(19)可得：

改变l的长度可得如下方程：

δy(ch)+l2εz(ch)-h1vh＝δdt3(22)

用式(22)减去式(19)可得：

将vh、εz(ch)代入式(19)可得：

当ch＝0即轴还未运动，运动角误差εx(ch)为0，由此可得：

v0＝εyc(25)

将式(13)和式(25)带入(8)式，可得：

εy(ch)＝wh-εxccosch+εycsinch(26)

将式(13)和式(25)带入(18)式，可得：

εx(ch)＝vh-εxcsinch-εyccosch(27)

(5)轴向几何误差参数识别

如图3(c)所示，同理可得，在坐标系中，ph′与dh之差为:

根据式(28)求得ph′与dh之间的距离表达式为:

根据式(29)可得：

式中，δds为球杆仪从初始位置到第h个位置的杆长变化量。

将式(30)两边同时平方化简可得：

δz(ch)-l(εy(ch)-εycsinch+εxccosch)＝δds(31)

由式(8)可知，将式(31)变为：

δz(ch)-lwh＝δds(32)

假定当前长度l为ls，因此得到：

δz(ch)＝δds+lswh(32)

式中，δds为球杆仪从初始位置到第h个位置的轴向杆长变化量，ls为l的取值。

至此，与c轴相关的八项误差参数全部辨识出，与位置点有关的跳动误差(δx(c)，δy(c)，δz(c))分别通过式(12)、式(24)和式(32)辨识出；颠摆和偏摆误差(εx(c)，εy(c))分别通过式(27)和式(26)辨识出；滚摆误差(εz(c))通过式(23)辨识出；与位置点无关的垂直度误差(εxc，εyc)分别通过式(13)和式(25)辨识出。

与现有技术相比，本发明具有以下优点：

本发明针对多轴数控机床c轴的结构和特点，根据球杆仪的工作原理，利用多体系统理论，建立了在径向、切向和轴向三种联动模式下带有几何误差的运动方程和理想状态下的运动方程，通过球杆仪的两端位置变化量，并将球杆仪的两端坐标分别表述到同一坐标系中，求出两点间的实际距离，从而建立理论模型与实际测量值的关系，实现了c轴8项几何误差参数的辨识。本发明辨识出了旋转c轴全部的误差项，解决了几何误差参数间存在的耦合现象，而且准确，快捷，辨识精度高，对实现多轴数控机床其余旋转轴的误差辨识都具有重大的理论意义和现实意义。

附图说明

图1为相邻两体运动关系示意图。

图2为c轴球杆仪测量示意图。

图3为c轴三种测量模式运动位置示意图；其中，(a)为切向运动位置示意图，(b)为径向运动位置示意图，(c)为轴向运动位置示意图。

具体实施方式

本发明所述方法由球杆仪进行测量实现。所述球杆仪安装有可伸缩的纤维杆内的高精度位移传感器，可用于检测纤维杆杆长的变化，从而通过采集的数据分析c轴的各项几何误差参数。

本发明所述方法具体包括以下步骤：

步骤1，根据多体系统理论，建立相邻两体运动关系方程；

步骤2，通过对机床旋转轴的分析，得到c轴的几何误差项，然后根据球杆仪的工作原理，得到c轴几何误差参数辨识的径向，切向，轴向三种测量模式运动方向。ah、bh、dh点为与刀具主轴连接端，由于运动时工作台(c轴)存在几何误差，因此工作台(c轴)上一点ph在实际运动过程中就会偏离理想位置ph点到达实际位置ph′点，phah、phbh、phdh分别是径向、切向、轴向测量的球杆仪理想位姿，且理论长度分别为dr、dt、ds，实际运动过程中phah、phbh、phdh变为了ph′ah、ph′bh、ph′dh。在工作台(c轴)建立参考坐标系和运动参考坐标系，得到ph、ah、bh、dh的位置坐标。

步骤3，根据步骤2的分析，进行径向几何误差参数识别，通过建立在坐标系中的实际点ph′得位置方程和理论点ah的位置方程得到二者之差与径向杆长的变化量的关系，辨识出与位置点有关的跳动误差δx(c)，与位置点无关的垂直度误差εxc；

步骤4，根据步骤2的分析，进行切向几何误差参数识别，通过建立在坐标系中的实际点ph′得位置方程和理论点bh的位置方程得到二者之差与切向杆长的变化量的关系，辨识出与位置点有关的跳动误差δy(c)和εz(c)，与位置点无关的垂直度误差εyc，通过结合步骤3建立的方程，辨识出与位置点有关的跳动误差εy(c)和εx(c)；

步骤5，根据步骤2的分析，进行轴向几何误差参数识别，通过建立在坐标系中的实际点ph′得位置方程和理论点dh的位置方程得到二者之差与切向杆长的变化量的关系，辨识出与位置点有关的跳动误差δz(c)。至此，c轴的8项误差全部辨识出来。