一种二维非紧致边界声散射的边界元计算方法与流程

本发明涉及声学领域，更具体的涉及一种二维非紧致边界声散射的边界元计算方法。

背景技术：

频域下，声学波动方程一般表示为

式中，为为laplace算子，ω、k、p和γ分别为圆频率、声学波数、声压和声源强度，且k＝ω/c0，c0为声速。

声波传播的空间中往往存在着固体边界，如果边界的几何特征尺寸大于或者接近于声波的波长，则边界是声学非紧致的，声源激发的噪声辐射到边界上时会产生散射效应。声传播的计算可以采用边界元方法，当声源位于y点、观察点位于x点时，对声学硬边界声散射，声学波动方程的解为

式中：g(x,y,ω)为频域自由空间格林函数，z为散射边界上的点。边界元方法的要点包括：首先，将固体边界离散成一系列网格单元，并假设每个网格单元上的散射声压大小相同；然后，将观察点置于散射边界上的z点，利用上述声学波动方程求解边界处的声散射p(z,y,ω)；最后，利用p(z,y,ω)和声学波动方程求解远场x点处的声场。边界元方法仅需离散固体边界，具有计算效率高的优点。但是在气动噪声问题中，边界层内的声源与固体边界的距离远小于边界网格单元的特征尺寸，此时同一边界网格单元上各点的声散射不相同，也就是说此时的网格单元不能当常单元处理，否则会使计算结果出现很大误差。为了提高计算精度，需要将边界网格加密，使边界网格的特征尺寸接近声源与固体边界的距离，这就需要大量的网格单元，导致计算效率非常低，从而限制了边界元方法在气动声学分析中的应用。

综上所述，现有技术中，存在传统边界元方法在声源非常靠近固体边界时声散射计算效率低的问题。

技术实现要素：

本发明实施例提供一种二维非紧致边界声散射的边界元计算方法，用以解决传统边界元方法在声源非常靠近固体边界时声散射计算效率低的问题。

本发明实施例提供一种二维非紧致边界声散射的边界元计算方法，包括：

建立边界元模型，将非紧致边界s离散成m个边界网格单元；

确定各边界网格单元的中心点zm、单位外法线方向n(zm)和面积s(zm)，以及声源的强度γ和圆频率ω；

在远离非紧致边界s外确定观察点x，根据边界各网格单元的中心点zm、单位外法线方向n(zm)和面积s(zm)，以及声源的强度γ和圆频率ω，通过公式(1)，确定声源趋于边界网格单元zn时非紧致边界s的散射声场p(x,zn,ω)；

根据声源趋于边界网格单元zn时非紧致边界s的散射声场p(x,zn,ω)，通过公式(2)，确定由声源点y产生的声波传播到观察点x的声场p(x,y,ω)；

所述公式(1)如下所示：

其中，m,n＝1,2,…,m为边界网格单元编号，m为网格单元总数；p(x,zn,ω)为声源趋于边界网格单元zn时观察点x的声场；p0(x,zn,ω)为声源趋于边界网格单元zn时向观察点x的直接声辐射，且p0(x,zn,ω)＝γg(x,zn,ω)，γ为声源强度，ω为圆频率；zm为边界上异于zn的网格单元中心点；g为频域自由空间格林函数；n(zm)为zm点处边界的单位外法线矢量，s(zm)为zm点所在的边界网格单元面积；s'为除去zn网格单元部分的边界面。

所述公式(2)如下所示：

其中，y为声源点；n＝1,2,…,m为边界网格单元编号，m为网格单元总数；zn为编号为n的网格单元中心点；n(zn)为zn点处边界的单位外法线矢量，s(zn)为zn点所在的边界网格单元面积；p0(x,y,ω)为声源点y向观察点x的直接声辐射，且p0(x,y,ω)＝γg(x,y,ω)，g为频域自由空间格林函数。

较佳地，所述公式(1)的求解过程包括：

a、将公式(1)离散成一系列代数线性方程组

hp(x,z,ω)＝p0(x,z,ω)(3)

其中，h矩阵的子项为

式中，m,n＝1,2,…,180为边界网格单元编号；zm和zn为编号为m和n的边界网格单元中心点；s(zm)为编号为m的网格单元面积，n(zm)为zm点处边界的单位外法线矢量，矩阵p(x,z,ω)和p0(x,z,ω)分别为

b、确定g(x,zn,ω)、g(zm,zn,ω)和对于二维声传播问题，

其中，和分别为0阶和1阶第一类hankel函数，j为虚数单位，k＝ω/c0为声学波数，ω为圆频率，c0为声速；

c、确定矩阵h；当m≠n时，

其中，

其中，φ为zn点与zm边界网格单元两个端点之间的夹角；

d、采用数值方法求解代数线性方程组(3)得到p(x,zn,ω)。

较佳地，所述公式(2)的求解过程包括：

a、确定g(x,y,ω)、g(zn,y,ω)和对二维声传播问题，

b、采用方程(15)确定

其中，

其中，φ为y点与zn边界网格单元两个端点之间的夹角；

c、利用公式(2)计算p(x,y,ω)。

本发明实施例中，提供一种二维非紧致边界声散射的边界元计算方法，与现有技术相比，其有益效果为：传统边界元方法在求解非紧致边界的声散射时将观察点置于边界上，当声源与边界的距离远小于单元网格的尺寸时，边界网格单元不能当常单元处理，使得计算结果不精确。本发明的边界元方法在求解非紧致边界的声散射时将声源置于边界上，当声源与边界的距离远小于单元网格的尺寸时，边界网格单元仍能当常单元处理，在相同边界网格离散条件下计算精度相对于传统边界元方法大大提高。

附图说明

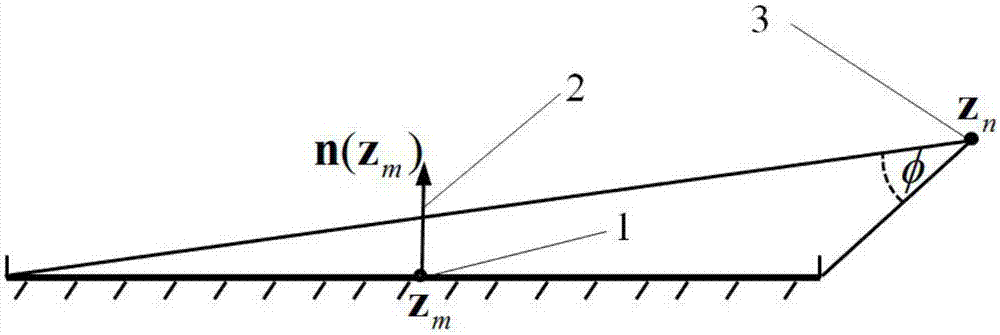
图1为zn点与zm网格单元端点夹角示意图；

图2为声源点y与zn网格单元端点夹角示意图；

图3为二维非紧致圆柱声散射示意图；

图4为圆柱声散射本专利边界元方法数值解、传统边界元方法数值解与理论解析解的远场声场指向性对比图。

附图标记说明：

1、zm网格单元；2、zm网格单元的外法线矢量；3、zn点；4、zn网格单元；5、zn网格单元的外法线矢量；6、声源点y；7、二维圆柱；8、观察点x；9、声源点y；10、圆柱表面上的点z；11、圆柱声散射空间指向性理论解析解；12、圆柱声散射空间指向性本专利边界元方法数值解；13、圆柱声散射空间指向性传统边界元方法数值解。

具体实施方式

下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。

本发明实施例以二维非紧致圆柱声散射为例，提供了的一种二维非紧致边界声散射的边界元计算方法，图1为zn点与zm网格单元端点夹角示意图；图2为声源点y与zn网格单元端点夹角示意图；图3为二维非紧致圆柱声散射示意图；图4为圆柱声散射本专利边界元方法数值解、传统边界元方法数值解与理论解析解的远场声场指向性对比图。

如图3所示，在空间中有一直径d＝100mm的二维圆柱，单位强度的单极子点声源位于x轴上的y点，其与圆柱表面的距离为d＝0.05mm，声源的圆频率为ω，观察点x与圆柱中心的距离为rx＝12800mm。

本实施例的具体过程包括以下步骤：

步骤1，划分网格，建立边界元模型。边界元模型需要将结构表面进行离散，本实施例中，二维圆柱结构简单，采用自编程序完成网格划分，将180个离散结点(m＝1,2,…,180代表编号为m的离散点)均匀布置在圆柱表面，从而将二维圆柱表面离散为180个线网格单元，其长度尺寸约为1.745mm，远大于声源与圆柱表面的距离0.05mm。

步骤2，提取各边界网格单元的中心点坐标zm、单位外法线方向n(zm)以及面积s(zm)，m＝1,2,…,180代表编号为m的网格单元。对于本实施列，坐标原点位于圆柱中心，提取的过程包括：

a.提取离散结点的坐标。从已建立好的边界元模型中，提取出各离散结点矢量的坐标，m＝1,2,…,180代表编号为m的离散点，和分别为第m个离散点在x和y轴方向的坐标值。

b.确定各线网格单元的中心点坐标。第m个线网格单元由离散点和决定，其中心点矢量的坐标为

c.确定各线网格单元的单位外法线方向矢量。第m个线网格单元单位外法线方向矢量的坐标为

d.确定各线网格单元的面积。对于第m个线网格单元，其面积等于该线网格单元的长度

步骤3，对观察点x和边界s上的点zn，采用边界元方法求解下述积分方程用于计算声源趋于zn点非紧致边界s的散射声场p(x,zn,ω)

其中，m,n＝1,2,…,180为边界网格单元编号；p(x,zn,ω)为声源趋于边界网格单元zn时观察点x的声场；p0(x,zn,ω)为声源趋于边界网格单元zn时向观察点x的直接声辐射，且p0(x,zn,ω)＝g(x,zn,ω)，ω为圆频率；zm为边界上异于zn的网格单元中心点；g为频域自由空间格林函数；n(zm)为zm点处边界的单位外法线矢量，s(zm)为zm点所在的边界网格单元面积；s'为除去zn网格单元部分的边界面。

具体计算过程如下：

a、将公式(1)离散成一系列代数线性方程组

hp(x,z,ω)＝p0(x,z,ω)(3)

其中，h矩阵的子项为

式中，m,n＝1,2,…,180为边界网格单元编号；zm和zn为编号为m和n的边界网格单元中心点；s(zm)为编号为m的网格单元面积，n(zm)为zm点处边界的单位外法线矢量，矩阵p(x,z,ω)和p0(x,z,ω)分别为

b、确定g(x,zn,ω)、g(zm,zn,ω)和对于二维空间的声传播问题，

其中，和h1⁽¹⁾分别为0阶和1阶第一类hankel函数，j为虚数单位，k＝ω/c0为声学波数，ω为圆频率，c0为声速；

c、确定矩阵h；当m≠n时，

其中，

其中，φ为zn点与zm边界网格单元两个端点之间的夹角，如图1所示。

d、采用数值方法求解代数线性方程组(3)得到p(x,zn,ω)。

步骤4，对观察点x和声源点y，利用下述公式(2)计算y点声源产生的声波传播到x点的声场p(x,y,ω)。

其中，y为声源点；n＝1,2,…,m为边界网格单元编号，m为网格单元总数；zn为编号为n的网格单元中心点；n(zn)为zn点处边界的单位外法线矢量，s(zn)为zn点所在的边界网格单元面积；p0(x,y,ω)为y点声源向x点的直接声辐射，且p0(x,y,ω)＝g(x,y,ω)，g为频域自由空间格林函数。

具体计算过程如下：

a、确定g(x,y,ω)、g(zn,y,ω)和对二维声传播问题，

b、采用方程(15)确定

其中，

其中，φ为y点与zn边界网格单元两个端点之间的夹角，如图2所示。

c、利用公式(2)计算p(x,y,ω)。

当声学波数k＝20时，声波波长与圆柱直径的比约为3，圆柱是声学非紧致的。在相同边界网格条件下，圆柱声散射本专利边界元方法数值解、传统边界元方法数值解与理论解析解的远场声场指向性对比如图3所示，其中曲线11是理论解析解结果，曲线12是本专利边界元方法数值解，曲线13是传统边界元方法数值解。传统边界元方法的结果与理论解析解存在显著的差异，而本专利边界元方法数值解与理论解析解结果一致，一方面证明了本发明方法的正确性，另一方面体现了本发明方法的优越性。

以上公开的仅为本发明的几个具体实施例，本领域的技术人员可以对本发明进行各种改动和变型而不脱离本发明的精神和范围，倘若本发明的这些修改和变型属于本发明权利要求及其等同技术的范围之内，则本发明也意图包含这些改动和变型在内。