一种内啮合齿轮轴减速器轮齿损伤故障的非线性动力学建模方法与流程

本发明属于机械系统可靠性工程技术领域，涉及一种内啮合齿轮轴减速器轮齿损伤故障的非线性动力学建模方法。

背景技术：

内啮合齿轮轴减速器具有结构紧凑、性能稳定和工作高效的优点，在民用、工业、航空和航天领域应用非常广泛，故对其工作机理的理论研究具有重要意义。减速器齿轮副工作时，即便是正常状态，由于齿面摩擦、齿侧间隙以及时变啮合刚度的影响，齿轮振动表现出很强的非线性特征。

为实现高精度、低噪声、低振动以及提高齿轮传动可控性的目标，研究人员在齿轮传动系统的非线性动力学问题上面投入了大量的时间和精力。轮齿的齿面点蚀、剥落和断齿等损伤是齿轮减速器的常见故障形式，故障的发生发展严重影响减速器的可靠性指标，甚至造成严重的财产和生命安全损失，其发生和发展机理一直是科技工作人员研究的重点。

内啮合齿轮轴减速器轮齿故障的非线性动力学的研究对齿轮减速器的理论和应用研究具有重要价值。

技术实现要素：

本发明为了揭示内啮合齿轮轴减速器的轮齿损伤故障发生发展机理的理论，通过研究减速器的齿面摩擦阻尼、齿侧间隙、时变啮合刚度对其动力学特性的影响，建立了包含齿面摩擦、非线性齿侧间隙函数和时变啮合刚度、轮齿损伤因子和啮合粘滞阻尼的内啮合齿轮轴减速器动力学模型，具体是一种内啮合齿轮轴减速器轮齿损伤故障的非线性动力学建模方法。

具体步骤如下：

步骤一、针对某个内啮合齿轮轴减速器，设定对该减速器进行建模的条件；

(1)该减速器的内齿轮和外齿轮均为渐开线直齿圆柱齿轮；

(2)轮齿故障是指减速器齿轮的齿面点蚀、剥落和断齿等损伤故障形式；

(3)两齿轮齿坯视为刚体，减速器的输入和输出轴视为刚体；两齿轮轴的支撑刚度足够大，不考虑支撑的弹性变形；

(4)减速器中各零部件均不受轴向力，振动矢量存在垂直于轴线的平面；

(5)主动轮(外齿轮)、从动轮(内齿轮)的轮齿做悬臂梁考虑，存在轮齿沿啮合线的相对滑动位移；

(6)轮系中齿轮按照标准中心距安装，齿轮节圆与分度圆重合；

(7)不计入零件加工误差与安装误差。

步骤二、针对该内啮合齿轮轴减速器，利用齿轮角位移确定齿轮副啮合线上的相对线位移；

其中：x是内齿轮啮合副上沿啮合线的相对线位移；y是外齿轮啮合副上沿啮合线的相对线位移；r1是外齿轮的分度圆半径；r2是内齿轮的分度圆半径；θ1是外齿轮的扭转角位移；θ2是内齿轮的扭转角位移；t是时间变量；e(t)是齿轮副的静态传动误差，e(t)＝easinωmt，ea为误差幅值，ωm为啮合齿频。

步骤三、根据内齿轮啮合副上沿啮合线的相对线位移确定非线性的齿侧间隙函数；

式中，b为齿侧间隙常数。

步骤四、采用傅里叶级数逼近健康状态下齿轮副的时变啮合刚度函数km(t)；

其中，kav是齿轮副平均啮合刚度，ka是刚度变化幅值；n取整数值。

步骤五、采用傅里叶级数逼近单个断齿故障处的轮齿时变啮合刚度函数k(t)

kaf是断齿处单齿啮合刚度变化的峰峰值，z1为外齿轮亦即主动轮的齿数；ω1是外齿轮的名义角速度；

步骤六、利用健康状态齿轮副的时变啮合刚度与单一断齿故障状态的轮齿时变刚度做差，并结合轮齿损伤因子，对轮齿损伤故障时变啮合刚度建模；

其中，kmf(t)是含有轮齿损伤故障的齿轮副时变啮合刚度；

ε为齿轮齿面损伤因子；ε∈[0,1]，定义如下：

步骤七、利用该减速器的齿侧间隙函数，结合轮齿损伤故障时变啮合刚度建模，采用lagrange方法，建立齿轮副的非线性动力学方程；

齿轮副的非线性动力学方程包括内啮合齿轮副的输入矩阵t1和输出矩阵t2；

其中：i1是外齿轮的转动惯量；i2是内齿轮的转动惯量；是外齿轮的瞬时角加速度；是内齿轮的瞬时角加速度；cm是啮合粘滞阻尼系数；l1是外齿轮的啮合摩擦阻尼力的力臂；l2是内齿轮的啮合摩擦阻尼力的力臂；λ是摩擦力方向系数，ω2是内齿轮的名义角速度；是外齿轮的瞬时角速度；是内齿轮的瞬时角速度；μ是齿面动摩擦系数；

步骤八、对齿轮副的非线性动力学方程进行线性变换和无量纲化处理，得到最终计入摩擦和齿侧间隙的轮齿损伤故障状态下内啮合齿轮副无量纲非线性动力学模型；

模型如下：

τ＝ωet；ωe是齿轮副当量固有频率，me是齿轮副当量质量，m1是外齿轮的质量，m2是内齿轮的质量；

ea是轮齿综合误差变化的幅值，是常数；

本发明的优点在于：

(1)一种内啮合齿轮轴减速器轮齿损伤故障的非线性动力学建模方法，基于lagrange方法建立了内啮合齿轮副的非线性动力学模型，本模型的通用性很好，可以做任意工况下的内啮合齿轮副的动力学数值仿真。

(2)一种内啮合齿轮轴减速器轮齿损伤故障的非线性动力学建模方法，引入轮齿损伤因子ε，可以对轮齿故障任意损伤程度的内啮合减速的振动信号输出进行数值模拟。

(3)一种内啮合齿轮轴减速器轮齿损伤故障的非线性动力学建模方法，模型中计入了摩擦阻尼效应、非线性齿侧间隙函数、时变啮合刚度等内部参数激励，数值仿真精度高，模型输出的齿轮减速器系统振动信号仿真程度高，非线性动力学特性明显。

附图说明

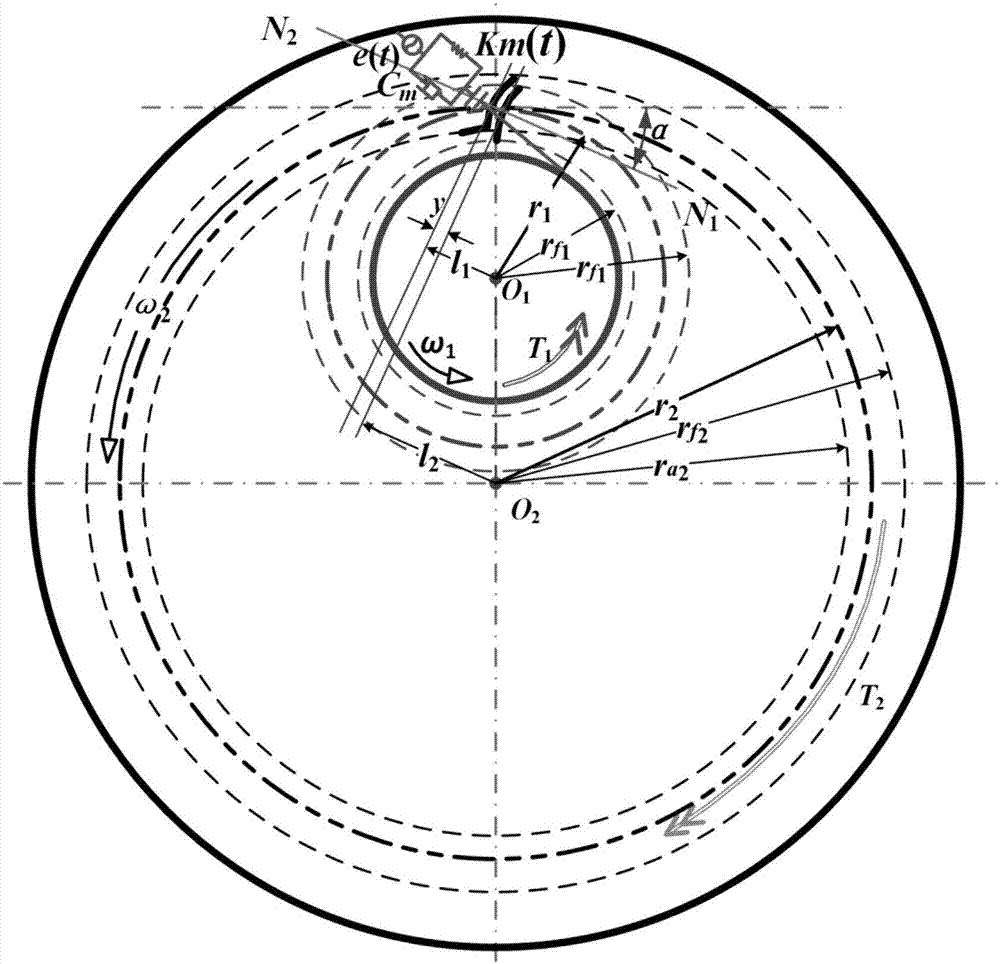
图1是本发明采用的内啮合齿轮轴减速器的结构示意图；

图2是本发明内啮合齿轮轴减速器轮齿故障非线性动力学模型原理示意图；

图3是本发明带有轮齿损伤故障的齿轮副时变啮合刚度波形示意图；

图4是本发明内啮合齿轮轴减速器轮齿损伤故障的非线性动力学建模方法流程图；

图5是本发明内啮合齿轮轴减速器轮齿健康状态稳态振动的相迹图；

图6是本发明本发明内啮合齿轮轴减速器轮齿健康状态稳态振动的时域图；

图7是本发明内啮合齿轮轴减速器轮齿健康状态稳态振动的频域图；

图8是本发明内啮合齿轮轴减速器轮齿轻微故障状态稳态振动的相迹图；

图9是本发明内啮合齿轮轴减速器轮齿轻微故障状态稳态振动的时域图；

图10是本发明内啮合齿轮轴减速器轮齿轻微故障状态稳态振动的频域图；

图11是本发明内啮合齿轮轴减速器断齿状态稳态振动的相迹图；

图12是本发明内啮合齿轮轴减速器断齿状态稳态振动的时域图；

图13是本发明内啮合齿轮轴减速器断齿状态稳态振动的频域图。

具体实施方式

下面将结合附图和实施例对本发明作进一步的详细说明。

本发明设计了一种包含齿面摩擦、非线性齿侧间隙函数、轮齿时变啮合刚度、轮齿损伤因子和啮合粘滞阻尼等因素的内啮合齿轮轴减速器的非线性动力学模型，针对的对象是某型内啮合齿轮轴减速器，基于lagrange方法，提出了计入摩擦和齿侧间隙的内啮合齿轮轴减速器轮齿损伤故障的非线性动力学建模方法。

如图1所示，为本实施例采用的某型内啮合齿轮轴减速器结构；建立的计入摩擦和齿侧间隙的轮齿损伤故障非线性动力学模型原理图如图2所示，

模型过程中用到的符号如表1所示：

表1

具体建模步骤如图4所示，包括如下：

步骤一、针对某个内啮合齿轮轴减速器，设定对该减速器进行建模的条件；

(1)该减速器的内齿轮和外齿轮均为渐开线直齿圆柱齿轮；

(2)轮齿故障是指减速器齿轮的齿面点蚀、剥落和断齿等损伤故障形式；

(3)两齿轮齿坯视为刚体，减速器的输入和输出轴视为刚性体；两齿轮轴的支撑刚度足够大，不考虑支撑的弹性变形；

(4)减速器中各零部件均不受轴向力，振动矢量存在垂直于轴线的平面；

(5)主动轮(外齿轮)、从动轮(内齿轮)的轮齿做悬臂梁考虑，存在轮齿沿啮合线的相对滑动位移；

(6)轮系中齿轮按照标准中心距安装，齿轮节圆与分度圆重合；

(7)不计入零件加工误差与安装误差。

步骤二、针对该内啮合齿轮轴减速器，利用齿轮角位移确定齿轮副啮合线上的相对线位移；

表示内啮合齿轮副的啮合线如图2中的n1n2；

其中：x是内齿轮啮合副上沿啮合线的相对线位移；y是外齿轮啮合副上沿啮合线的相对线位移；r1是外齿轮的分度圆半径，是常值；r2是内齿轮的分度圆半径，是常值；θ1是外齿轮的瞬时角位移，是关于t的函数；θ2是内齿轮的瞬时角位移，是关于t的函数；t是时间变量；e(t)是齿轮副的静态传动误差，e(t)＝easinωmt，ea为误差幅值，ωm为啮合齿频。

步骤三、根据内齿轮啮合副上沿啮合线的相对线位移确定非线性的齿侧间隙函数；

式中，b为齿侧间隙常数。

步骤四、采用傅里叶级数逼近健康状态下齿轮副的时变啮合刚度函数km(t)；

其中，kav是齿轮副平均啮合刚度，ka是刚度变化幅值；n取整数值。

如图3a所示，正常状态齿轮啮合刚度，啮合周期t0下，啮合刚度变化的峰峰值ka；啮合刚度变化的平均值为kav；

步骤五、采用傅里叶级数逼近单个断齿故障处的轮齿时变啮合刚度函数k(t)

kaf是断齿处单齿啮合刚度变化的峰峰值，z1为外齿轮也是主动轮的齿数，为常值；ω1是外齿轮的名义角速度，为常值；

如图3b所示，齿面单一断齿故障时的啮合刚度，旋转周期tz下，z1为主动齿轮的齿数；断齿啮合刚度变化的平均值为kav1；

步骤六、利用健康状态齿轮副时变啮合刚度与单一断齿故障状态的轮齿时变刚度做差，并结合轮齿损伤因子，对轮齿损伤故障时变啮合刚度建模；

其中，kmf(t)是含有轮齿损伤故障的齿轮副时变啮合刚度；

ε为齿轮齿面损伤因子；ε∈[0,1]，定义如下：

如图3c所示，断齿处单齿啮合刚度变化的峰峰值kavf＝kav-kav1。

步骤七、利用该减速器的齿侧间隙函数，结合轮齿损伤故障时变啮合刚度建模，采用lagrange方法，建立齿轮副的非线性动力学方程；

齿轮副的非线性动力学方程包括内啮合齿轮副的输入矩阵t1和输出矩阵t2；输入矩阵也是驱动转矩用；输出矩阵也是负载转矩用；

其中：i1是外齿轮的转动惯量，为常值；i2是内齿轮的转动惯量，为常值；是外齿轮的瞬时角加速度；是内齿轮的瞬时角加速度；cm是啮合粘滞阻尼系数；l1是外齿轮的啮合摩擦阻尼力的力臂，为常值；l2是内齿轮的啮合摩擦阻尼力的力臂，为常值；λ是摩擦力方向系数，ω2是内齿轮的名义角速度；是外齿轮的瞬时角速度，是t的函数；是内齿轮的瞬时角速度，是t的函数；μ是齿面动摩擦系数；

步骤八、对齿轮副的非线性动力学方程进行线性变换和无量纲化处理，得到最终计入摩擦和齿侧间隙的轮齿损伤故障状态下内啮合齿轮副无量纲非线性动力学模型；

无量纲化过程常用到的代数表示包括τ、ζ1、ζ2、k2、fav、fe；符号和参数之间的转换关系如表2所示；

表2

模型如下：

τ＝ωet；ωe是齿轮副当量固有频率，me是齿轮副当量质量，m1是外齿轮的质量，m2是内齿轮的质量；

ea是轮齿综合误差变化的幅值，是常数；

实施例

对某型带有轮齿损伤故障的内啮合齿轮轴减速器进行了建模仿真试验，得到了其纯扭转振动的仿真结果，获得了传动系统的相迹图、时域图和频域图，并据此研究了摩擦和啮合刚度对系统振动的影响。根据扭转振动曲线，提取到了故障的特征值并描绘出特征值曲线。仿真实例的参数如下表所示。

内啮合齿轮减速器仿真实例参数取值表

在实际仿真过程中，轮齿损伤因子ε分别取值0/0.2/1，模拟轮齿正常状态/齿面轻微损伤/轮齿折断共3种健康/故障状态；得到了3种状态下内啮合齿轮减速器振动的相迹、时域和频域曲线，较好地反映的各状态下的振动特性。

1)ε＝0时正常齿轮振动

ε＝0时，轮齿健康状态良好，齿轮副无齿面损伤故障，此时齿轮振动稳态响应的相迹如图5所示，由健康状态的稳态曲线图中可以看出，正常齿轮振动时，如图6所示，时域曲线平稳啮合周期为20，频域图如图7所示，只有啮合频率0.048及其高次倍频，没有边频带，相迹周期运动。

2)ε＝0.2齿面轻微损伤

ε＝0.2时，即表示轮齿早期裂纹、点蚀和剥落等轻微故障，此时齿轮系统的数值求解曲线中表现出齿轮齿面轻微故障稳态响应，其相迹如图8所示。由轻微故障状态下的稳态曲线图中可以看出齿轮点蚀振动时，时域图如图9所示，时域曲线出现低频波动，频域图如图10所示，有啮合频率0.111及其高次倍频，啮合频率处出现轻微边频带，边频带间隔为转频0.008，相迹周期运动。

3)ε＝1断齿故障

ε＝1时，表示有齿轮系统中存在断齿故障。此时齿轮系统的数值求解曲线中表现出断齿故障状态下的稳态响应。其相迹如图11所示，由断齿状态下的稳态响应曲线可以看出，齿轮断齿振动时，时域曲线如图12所示，时域曲线出现明显冲击调制现象，周期即为旋转周期，频域曲线如图13所示，频域图中有啮合频率0.111及其高次倍频，啮合频率处出现明显的边频带，边频带间隔为转频0.2586，相迹周期运动不明显。