一种桥梁风振监测传感器布置和风振响应重构方法与流程

本发明属于土木工程和桥梁监测领域，具体涉及一种桥梁风振监测传感器布置和风振响应重构方法。

背景技术：

随着桥梁建造技术的提高和社会经济的发展，同时为了满足现代化交通运输和快速出行的要求，一大批大跨桥梁在全国各地建成并投入使用，如润扬长江大桥、杭州湾大桥、港珠澳大桥、矮寨大桥等。这些桥梁具有跨度大、结构柔、桥塔高和重量轻的特点，且所处的地理环境特别复杂，极易遭受各种强风的袭击。而强风引起的振动响应成为影响桥梁行车舒适性和结构安全性的主要因素之一。对桥梁的风致振动响应进行实时监测就显得非常必要，运用实时监测数据可准确把握桥梁风致振动响应的规律，为桥梁运营状态评估提供数据支撑，确保桥梁在风荷载作用下的安全。

由于大跨桥梁结构的复杂性，桥梁风致振动监测的可选节点可能达到几百个甚至上千个。但受到振动监测技术和振动监测成本的限制，无法对桥梁结构所有节点的风致振动响应都进行监测。那么，如何从成百上千的可选节点中选择最有价值的节点进行监测，就成为桥梁风致振动监测亟待解决的关键技术问题。已有的振动传感器布置方法主要针对桥梁在环境激励或者车辆荷载作用下的振动响应监测，仅考虑桥梁本身的动力特性。由于风荷载的非平稳性和桥梁响应的非线性特征，桥梁结构在风荷载作用下的振动响应与环境激励或者车辆荷载作用下的振动响应相比，存在很大的差异。利用已有的振动传感器布置方法进行风致振动监测传感器布置，难以准确捕捉桥梁风致振动响应的典型特征。不仅如此，由于风致振动监测传感器数量的有限性，无法全面掌握桥梁风致振动响应信息。通过测点的风致振动数据对全桥的风致振动响应进行重构，进而获得其余节点的风致振动响应，是全面了解桥梁风致振动响应特征的有效手段。然而，目前尚未提出有效的桥梁风致振动响应重构方法。

因此，提出一种能够对桥梁关键风振响应进行监测的传感器布置方法，并建立基于测点风致振动响应信息的风振响应重构方法，对于全面把握桥梁的风致振动响应特征具有重要的工程意义和实用价值。

技术实现要素：

发明目的：为了克服现有技术中存在的不足，本发明提供一种桥梁风振监测传感器布置和风振响应重构方法，它能从桥梁所有可选节点中选择最有价值的位置进行风致振动监测传感器布置，并能根据测点的风致振动响应重构桥梁所有节点的风振响应，进而得到桥梁所有节点的风振响应。

技术方案：为解决上述技术问题，本发明的一种桥梁风振监测传感器布置和风振响应重构方法，包括桥梁风致振动监测传感器布置方法和桥梁风致振动形态重构方法。

其中，桥梁风致振动监测传感器布置方法包括以下步骤：

步骤1，根据风致振动时域分析方法计算得到桥梁在设计风荷载作用下的振动响应，绘制关于加速度的风振响应曲线；

步骤2，利用相邻节点之间风振加速度差的符号进行风振响应曲线拐点的判断，找出风振响应曲线拐点最多的时刻；

步骤3，选取该时刻风振响应曲线的拐点和拐点之间的中间节点作为传感器布置位置，得出桥梁风振监测传感器布置方案；

桥梁风致振动响应重构方法是在完成上述桥梁风致振动监测传感器布置方法后，实施步骤4，采用正弦函数加权和作为风振响应形态函数，利用测点的风振加速度进行风振响应形态函数的待定参数拟合，实现桥梁风振响应的重构，最终得到桥梁所有节点的风振响应。

有益效果：本发明选择风振响应曲线的拐点和拐点之间的中间节点布置传感器，能够保证有限数量的振动传感器捕捉到桥梁在任意时刻的最大风振响应和最小风振响应；同时利用有限测点的风振响应和正弦函数加权和组成的形态函数进行桥梁所有节点的风振响应重构，能够获得桥梁所有节点的风振响应。保证了监测传感器在任意时刻均能捕捉到桥梁风振加速度的最大值和最小值，同时能够利用测点加速度重构出桥梁所有节点在任意时刻的风振加速度，实现桥梁风振响应的全面把握。本发明采用流程化设计，操作简单，便于工程人员进行桥梁风致振动监测的传感器布设和风振响应重构，为桥梁风致振动监测提供了一种有效方法，因此具有广阔的工程应用前景。

附图说明

图1是本发明实施例的流程图；

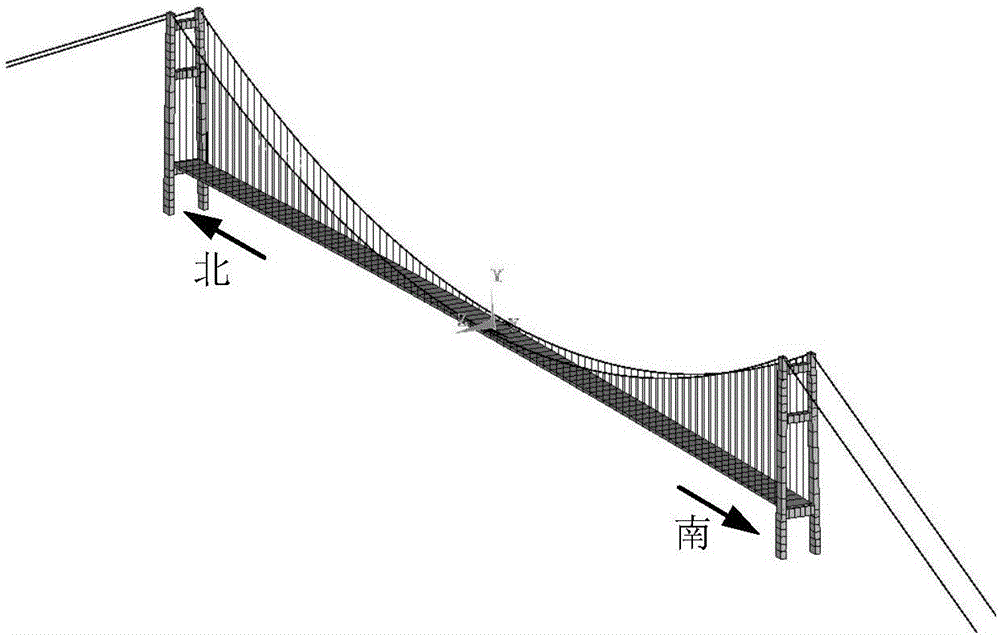
图2是本发明所述实施例涉及的悬索桥有限元模型；

图3是本发明所述实施例涉及的悬索桥跨中节点竖向风致振动加速度时程；

图4是本发明所述实施例涉及的悬索桥主梁第2350秒的风振响应曲线；

图5是本发明所述实施例涉及的悬索桥主梁第2350秒风振响应曲线的拐点；

图6是本发明所述实施例涉及的悬索桥主梁第3133秒风振响应曲线和拐点；

图7是本发明所述实施例涉及的悬索桥主梁第3133秒风振响应曲线的拐点和中间节点；

图8是本发明所述实施例涉及的悬索桥主梁风振监测传感器布置方案；

图9是本发明所述实施例涉及的悬索桥主梁第3133秒的实际振动响应和重构振动响应；

图10是本发明所述实施例涉及的悬索桥主梁第1500秒的实际振动响应和重构振动响应；

图11是本发明所述实施例涉及的悬索桥主梁第1780秒的实际振动响应和重构振动响应。

具体实施方式

实施例：

本实施例的实施流程如图1所示，包括桥梁风致振动监测传感器布置方法和桥梁风致振动响应重构方法。

其中，桥梁风致振动监测传感器布置方法包括以下步骤：

(1)根据被测桥梁的设计方案，利用梁单元和杆单元，采用大型通用有限元软件建立被测桥梁的有限元模型，假定有限元模型的节点数为n。设被测桥梁风致振动响应监测的可选测点为有限元模型的节点，即被测桥梁可选的用于风致振动响应监测的节点数量为n。

(2)基于被测桥梁的设计规范，根据被测桥梁的场地条件，选择用于被测桥梁设计的风荷载模型，利用线性滤波法模拟得到用于被测桥梁风振响应计算的风荷载时程，风荷载时程的样本数量为m，采样间隔为δt。

(3)将模拟风荷载时程输入有限元模型，采用风致振动时域分析方法计算被测桥梁所有可选测点的风致振动响应时程。

(4)构造被测桥梁风致振动响应向量，第t时刻的风致振动响应向量φt为

φt＝(at，1，at，2，…，at，n)(1)

其中，at，n(n＝1，2，…，n)表示第t时刻(t＝1，2，…，m)第n个节点的风致振动加速度。

(5)以风致振动加速度为纵坐标，以节点编号为横坐标，绘制桥梁不同时刻的风振响应曲线。

(6)计算第t时刻被测桥梁相邻节点之间的振动加速度差：

其中，表示在第t时刻节点r+1与节点r之间的风致振动加速度差。

(7)计算第t时刻被测桥梁振动响应曲线的拐点数目kt和拐点集合dt。如果小于或者等于0，表明节点s+1为拐点；反之，如果大于0，表明节点s+1不是拐点。拐点数目kt和拐点集合dt为

其中，sgn(·)表示符号函数，nt，v(v＝1，2，…，kt)表示第t时刻被测桥梁振动响应曲线的第v个拐点对应的节点编号。

(8)重复步骤(6)和(7)，直至所有时刻的拐点数目和拐点集合计算完成。

(9)计算被测桥梁振动响应曲线的拐点数目最大值kmax。

kmax＝max(kt)(5)

(10)确定拐点数目最大值kmax对应的时刻为tmax，根据tmax时刻的拐点集合计算拐点之间的中间节点编号

其中，rmax，j(j＝1，2，…，kmax-1)表示tmax时刻拐点和拐点之间的中间节点编号，表示向下取整；如果rmax，j等于表明拐点和拐点之间没有中间节点；中间节点组成中间节点集合rmax

(11)合并拐点集合和中间节点集合rmax，组成风致振动监测节点集合。

(12)在风致振动监测节点集合上布置风致振动监测传感器，得到风致振动监测传感器布置方案。

桥梁风致振动响应重构方法，包括以下步骤：

(1)设风致振动监测传感器集合为s＝(ｓ1，s2，…，sw)，其中w为风致振动监测传感器的数量；监测节点对应的集合为其中表示第sp个传感器布置的节点；节点的风振加速度响应为选取有限元模型中的任意一个节点作为参考点，节点距离参考点的距离为

(2)选取风致振动响应形态函数为

其中，a(x)表示距离参考点距离为x处的风振加速度响应，x表示距离，sin(·)表示正弦函数，αk、βk和γk为待定参数。

(3)根据测点距离参考点的距离和测点的加速度响应，利用非线性最小二乘法拟合式(9)中的待定参数，建立被测桥梁的风致振动响应形态函数，得到被测桥梁所有节点的风致振动响应。

下面以一大跨悬索桥主梁的竖向风致振动响应监测为例，说明如何实现桥梁风振监测传感器布置和风振响应重构。

根据该桥的设计图纸，采用ansys软件，利用梁单元和杆单元建立该桥的有限元模型，如图2所示。主梁采用梁单元模拟，离散为93个节点，由北向南依次编号为1，2，...，93，相邻节点之间的距离为16.1m。基于被测桥梁的设计规范，根据被测桥梁的场地条件，选定用于该桥设计的风荷载模型为：

其中，su(n)表示顺风向风功率谱密度函数，ω表示风的脉动频率，f表示莫宁坐标(f＝(ω×69.3)/(6.93^1.2×27.1))。

利用线性滤波法模拟得到被测桥梁风致振动响应计算的风荷载时程，风荷载时程的样本数量为3600，采样间隔为1秒。将模拟风荷载时程输入有限元模型，采用风致振动时域分析方法计算被测桥梁所有可选测点的风致振动响应时程。主梁跨中节点的竖向风致振动加速度时程如图3所示。

以第2350秒为例说明如何得到风振响应曲线的拐点数目和拐点集合。构造主梁的风致振动响应向量φ2350，绘制风振响应曲线，如图4所示。利用式(2)计算相邻节点之间的振动加速度差利用相邻节点加速度差的乘积判断拐点，得到第2350秒主梁风致振动响应曲线的拐点，如图5所示。通过式(3)计算得到拐点数目k2350为5，通过式(4)得到拐点位置集合d2350：

d2350＝(2237475772)(11)

利用式(5)计算主梁风致振动响应的拐点数目最大值kmax及其对应的时刻tmax：

kmax＝15(12)

tmax＝3133(13)

第3133秒主梁风致振动响应曲线如图6所示，拐点集合d3133为

d3133＝(3411192531384756636975839091)(14)

利用式(6)计算中间节点的编号，第3133秒中间节点如图7所示。利用式(7)计算中间节点集合r3133

r3133＝(71522283442515966727986)(15)

合并拐点集合d3133和中间节点集合r3133，得到该桥主梁风致振动监测的传感器布置方案如图8所示。

假定采用有限元模型和风致振动时域分析方法计算得到的风致振动响应为该悬索桥的实际风振响应。采用图8所示的传感器布置方案进行风致振动响应监测，则测点的位置和测点处的风致振动加速度已知。

以1号节点为参考点，计算主梁上其余92个节点距离参考点的距离。

利用式(8)计算得到u为9，以测点的风致振动加速度和测点距离参考点的距离为已知量，利用式(9)的风致振动响应形态函数对主梁的风致振动响应进行重构。

利用非线性最小二乘法进行拟合，可得风致振动响应形态函数中待定参数的取值。

第3133秒主梁的实际振动响应和重构振动响应对比如图9所示，拟合误差为3.24×10^-5，重构的风致振动响应形态函数为：

任选第1500秒，主梁的实际振动响应和重构振动响应对比如图10所示，拟合误差为7.74×10^-6，重构的风致振动响应形态函数为：

任选第1780秒，主梁的实际振动响应和重构振动响应对比如图11所示，拟合误差为3.24×10^-5，重构的风致振动响应形态函数为：

从图9、图10和图11可以看出，使用本发明的桥梁风振监测传感器布置方法进行传感器布置，传感器能有效捕捉被测桥梁在任意时刻的风致振动加速度响应的最大值和最小值；不仅如此，重构的振动响应与实际的振动响应非常接近，误差很小。因此，可以利用本发明的方法进行桥梁风致振动监测传感器布置和振动响应重构，得到桥梁所有节点的风致振动响应。