一种多源数据融合的航空涡扇发动机剩余寿命预测方法与流程

本发明涉及航空涡扇发动机剩余寿命预测领域，具体是一种多源数据融合的航空涡扇发动机剩余寿命预测方法。

背景技术：

航空发动机预测与健康管理技术(prognosticsandhealthmanagement，phm)为发动机视情维修(condition‐basedmaintenance，cm)提供技术指导和先验知识，大力推动了航空发动机维修技术逐渐由定时维修向视情维修技术的转变，确保飞行安全、降低维修费用，因此引起了广泛的关注和研究。随着传感器技术和电子设备的进步，发动机原始监测数据能够被准确的监测和记录，为phm技术提供了足够的数据支持。如何根据已有的发动机原始监测数据，对发动机剩余寿命进行准确的预测，是航空发动机phm技术的研究核心。

基于统计数据驱动的方法通过挖掘监测数据包含的潜在信息，以显示系统内部变化以及外部环境影响所导致系统的性能变化，避免了对复杂精密度高的航空发动机系统机理进行建模，同时兼顾预测准确性，直接实现涡扇发动机的寿命预测，使得预测结果具有模糊性，为今后的研究中，融入专家知识进行更精确的预测提供可行性。统计数据驱动方法需要对系统退化过程建模，维纳过程符合系统非线性非平稳退化过程，同时具有良好的数学特性，基于维纳过程的退化模型已经在航空发动机系统退化建模分析和剩余寿命预测等方面取得了不错的成效，充分证明了该模型的适用性。

在实际应用中，航空发动机的排气温度裕度作为一项表征发动机换发依据和重要的性能指标，常被用于建立发动机退化模型。基于线性漂移的维纳过程概率分布函数明确，模型简单。然而，在现有的航空发动机剩余寿命研究中，却忽略了其他监测数据中携带的部件状态信息、发动机运行环境和个体之间的差异性以及发动机系统运行后期退化加速的特点，没有同时考虑多源的监测数据和带非线性漂移退化过程的结合。

技术实现要素：

针对传统的航空发动机剩余寿命预测方法的不足，本发明通过提供一种多源统计数据驱动的航空涡扇发动机剩余寿命预测方法，以解决传统统计数据驱动预测方法中忽略发动机多维监测数据和设备运行环境及个体差异的问题。

为实现上述目的，本发明的构思与技术解决方案实现如下：

本发明的基本构思是，充分利用发动机传感器采集的有效监测数据，在不利于寿命预测冗余特征的基础上，进行信息融合以提取表征发动机运行状态的健康指标和失效阈值，解决传统预测方法中监测数据信息利用不充分的问题。建立基于带随机参数的非线性维纳过程航空发动机失效模型，用以表征运行环境的不确定性以及设备个体间的差异性，模拟发动机的非线性退化过程。在此基础上，对航空发动机进行实时在线寿命预测。

基于上述基本构思，本发明提供的技术解决方案为一种多源数据融合的航空涡扇发动机剩余寿命预测方法，包括以下步骤：

步骤1：基于多源信息融合的涡扇发动机性能退化评估：

步骤1.1：多源监测数据降维，基于共同主成分分析法提取系统监测数据的主成分；监测数据为多维时间序列，保持时间维不变，对变量维进行共同主成分提取；

其中u＝[u1,u2,...,ur]^t为变换矩阵，r表示所选取主分量的数目，ur为第r个主分量对应的单位特征向量，xn为第n台航空发动机原始监测数据，为基于共同主成分分析降维后的第n台航空发动机监测数据，mn为第n台发动机的最大采样次数，为第n台航空发动机降维后第j次采样的监测数据，为第n台航空发动机降维后第mn次采样的监测数据，(·)^t表示转置。

步骤1.2：在步骤1.1的基础上，进行发动机健康参数的统计，研究表明发动机的前5％寿命周期被视作没有发生退化，故提取训练集中的未退化监测数据视作发动机的健康参数；

发动机总体健康参数为h＝(h1,h2,...hn,...,hn)^t，hn为第n台航空发动机健康参数，n为训练集中发动机台数；则航空发动机未退化监测数据均值m表示如下：

其中m为航空发动机未退化监测数据均值，sn表示训练集中第n台航空发动机健康参数的最大采样次数，为第n台航空发动机降维后第j次采样的监测数据，n为训练集中发动机台数，∑表示求和；

步骤1.3：在步骤1.2的基础上，计算发动机运行健康指标，以评估发动机性能退化程度；

每台发动机的健康指标计算公式如下：

其中tj为第n台发动机第j次采样的时间，yn(tj)为第j次采样时第n台发动机健康指标，m为航空发动机未退化监测数据均值，为第n台航空发动机降维后第j次采样的监测数据；

步骤1.4：基于发动机健康指标，确定发动机失效阈值；研究表明，航空发动机失效过程划分为四个阶段，最后一阶段视作发动机失效阶段；计算最后一类的聚类中心作为发动机失效阈值ω；

步骤2：航空发动机退化建模及参数估计；

步骤2.1：选取带非线性漂移的维纳过程为表征发动机退化过程模型，令初始退化状态为零；

y(t)＝y(0)+at^b+σb(t)(7)

其中，y(0)＝0，t为采样时间，非线性漂移部分为at^b，扩散系数为σ，b(t)为布朗运动；为表征制造偏差和运行环境导致发动机个体之间的差异性，a为非线性漂移部分的随机变量，满足其中n(·)表示正态分布，μa为随机变量a的均值，σa为随机变量a的标准差；同时将b定义为非线性漂移部分的常量表征发动机的相同特性；

步骤2.2：基于最大似然法的航空发动机退化模型参数估计：在建立涡扇发动机的退化模型后，需要基于发动机健康指标对模型进行参数估计；每台发动机在多个采样点的健康指标服从多维正态分布，故yn～n(μn,σn)，其中yn为第n台发动机的健康指标，μn为第n台发动机的健康指标均值向量；σn为第n台发动机的健康指标协方差矩阵；

对于不同发动机样本而言，退化过程独立同分布，因此关于总体发动机健康指标y的似然函数的自然对数形式如公式(12)所示：

其中a为非线性漂移部分的随机变量，μa为随机变量a的均值，σa为随机变量a的标准差，σ为扩散系数，b为非线性漂移部分的常量，y为总体发动机健康指标，n为训练集中发动机台数，mn为第n台发动机的最大采样次数，σn为第n台发动机的健康指标协方差矩阵，|·|表示取模操作，为σn的逆矩阵，yn为第n台发动机的健康指标，μn为第n台发动机的健康指标均值向量；

通过最大化似然函数进行参数估计；

其中a为非线性漂移部分的随机变量，μa为随机变量a的均值，σa为随机变量a的标准差，σ为扩散系数，b为非线性漂移部分的常量，为μa的估计值，n为训练集中发动机台数，tj为第n台发动机第j次采样的时间，σn为第n台发动机的健康指标协方差矩阵，σn为第n台发动机的健康指标协方差矩阵，|·|表示取模操作，为σn的逆矩阵，yn为第n台发动机的健康指标，y为总体发动机健康指标；

步骤3：建立航空发动机剩余寿命预测模型；

步骤3.1：基于维纳过程的航空发动机剩余寿命描述

基于发动机性能退化模型具有时间平移不变性，则退化模型表示为：

其中tc为航空发动机当前运行时间，li为航空发动机剩余寿命，b(·)表示布朗运动，y(tc)为航空发动机当前健康指标，y(li+tc)为航空发动机失效时的健康指标，a为非线性漂移部分的随机变量，b为非线性漂移部分的常量，σ为扩散系数，y(li)表示发动机随航空发动机剩余寿命li退化的维纳过程，∫表示积分；可知发动机剩余寿命描述仍可表征为带非线性漂移的维纳过程；

步骤3.2：航空发动机剩余寿命描述转换为标准维纳过程，对于非线性扩散过程，若满足：

其中μ(y,li)表示非线性漂移部分，σ′(li,u)为扩散部分，y为健康指标，li为航空发动机剩余寿命，c1(li)和c2(li)为任意关于li的函数，z为维纳过程初始值，∫表示积分，表示偏导数；

步骤4：基于性能衰退的航空发动机剩余寿命预测；

建立航空发动机剩余寿命概率密度函数模型，在步骤1、2、3的基础上，进行实时在线寿命预测；

布朗运动首次穿过失效阈值的概率密度函数表示如下：

其中pb(t)(ω,t)表示布朗运动首次穿过失效阈值的概率密度函数，ω为失效阈值，t为采样时间；

故航空发动机的剩余寿命概率密度函数为：

其中表示退化过程首次穿过阈值的概率密度函数，ω为失效阈值，li为航空发动机剩余寿命，tc为航空发动机当前运行时间，y(tc)为航空发动机当前健康指标，a为非线性漂移部分的随机变量，μa为随机变量a的均值，σa为随机变量a的标准差，f(a)为随机变量a的概率密度函数，b为非线性漂移部分的常量，σ为扩散系数，exp(·)表示以e为底的指数函数；以上结果满足航空发动机寿命预测的实际使用需要。

步骤1.4所述计算最后一类的聚类中心作为发动机失效阈值ω，具体步骤如下：

第一步，对于第n台发动机健康指标每次采样的健康指标视作一个样本；

第二步，随机选择4个初始聚类中心z1(k),z2(k)…z4(k)，k表示迭代次数，初始值为1，每迭代一次加1；

第三步，逐个将yn(tp),p＝1,2,...,mn按最小距离准则分配到4个中心为zi(k)的类中；

第三步，分计算各类的新中心：nj即第j类中的样本个数，oj表示属于第j类的样本集合；

第四步，如果zj(k+1)≠zj(k)则转到第2步，将模式重新分类，重复迭代计算，直到聚类中心收敛，记录4个聚类中心的最大值ωmax(n)；

第五步，对于每一台发动机，重复第1、2、3、4步，选取ωmax(n)中的最小值，视作发动机失效阈值，即ω＝min(ωmax(n)),n＝1,2,...,100,其中min(·)表示取最小值。

本发明的有益效果在：

本发明多源数据融合的航空涡扇发动机剩余寿命预测方法，基于多源监测数据，采用共同主成分分析提取监测数据的主成分，降低冗余数据和噪声数据的影响。多参数的融合能够最大限度利用传感器监测的有效信息，从而准确表征航空发动机的退化过程。发动机退化后期退化过程加速，为此建立带非线性漂移的维纳过程。建立航空发动机剩余寿命预测模型，实现对发动机的实时在线预测，为视情维修提供先验知识，具备良好的工程应用价值。

附图说明

图1为本发明方法流程图。

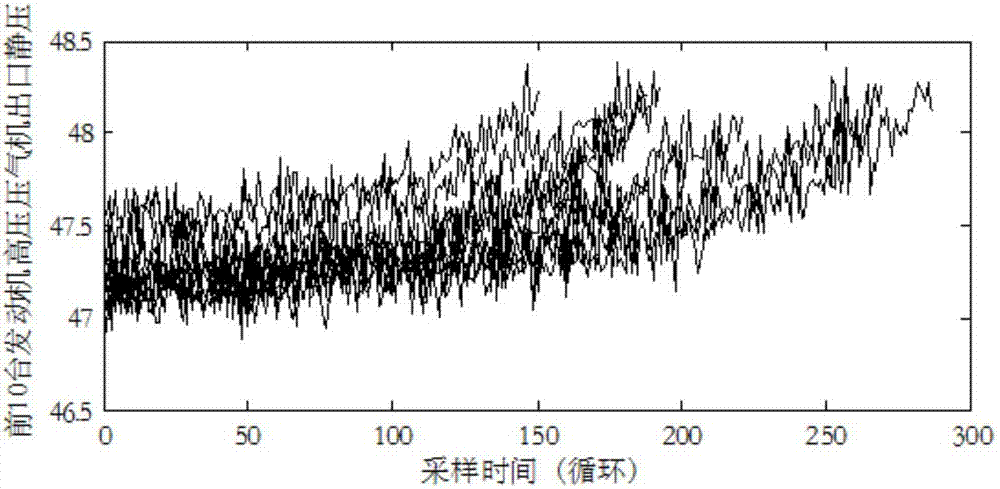
图2为训练集#1～#10台航空发动机高压压气机入口总温度测量数据。

图3为经共同主成分分析降维后前六主分量取值。

图4a为#1号训练发动机基于ed的发动机健康指标曲线。

图4b为#3号训练发动机基于ed的发动机健康指标曲线。

图5为航空发动机退化过程4个阶段。

图6为#1，#5，#10，#26，#60五台测试发动机剩余寿命概率密度函数和预测剩余寿命，以及真实剩余寿命的对比。

图7为剩余寿命误差区间示意。

图8为测试机中100台发动机剩余寿命频数分布

图9为测试机中100台发动机剩余寿命预测惩罚函数得分

具体实施方式

下面通过一组由nasa于2008年发布c‐mapss数据集来验证本发明提出的方法。该数据集利用涡扇发动机仿真模型，在不同操作条件下，模拟产生不同程度的特定失效状况时涡扇发动机原始监测数据。数据集主要分训练数据集、测试数据集、剩余寿命数据集三部分。其中，训练数据集中采集了100台涡扇发动机从健康状态运行至失效状态的全部监测数据。测试数据集包含有100台发动机的监测数据，均从健康状态开始运行，在系统失效前的某时刻停止采集。剩余寿命数据集记录了测试发动机的真实剩余寿命。以#1～#10台航空发动机的高压压气机入口总温度测量数据为例，训练集监测数据如图2所示。

实施例：

如图1所示，本发明基于多源统计数据驱动的航空涡扇发动机剩余寿命预测方法，包括以下步骤：

1、基于多源信息融合的涡扇发动机性能退化评估，采用共同主成分分析和基于欧氏距离(euclideandistance，ed)融合方法，在去除噪声干扰及不相关监测数据的条件下，融合发动机有效特征信息，获取总体发动机健康指标y。

1.1、多源监测数据降维，基于共同主成分分析法提取系统监测数据的主成分。监测数据为多维时间序列，保持时间维不变，对变量维进行共同主成分提取。

第n台航空发动机原始监测数据n＝(1,2,3,..,n)，xni为第n台航空发动机第i次采样的原始数据，n为训练集中发动机台数，本实施例中n＝100，mn为第n台发动机的最大采样次数。xni＝[xn1,xn2,...,xnj,...xnk]，k表示原始监测数据的维数，本实施例所使用的的数据集中原始监测数据的维数为21，故k＝21，xnj为第n台发动机第i次采样数据中第j个传感器测量数据。

对于训练数据集，基于共同主成分分析法获取每台发动机的协方差矩阵，公式如下：

cn＝e[(xn-e(xn))^t(xn-e(xn))](1)

其中cn为第n航空台发动机的协方差矩阵，xn为第n台航空发动机原始监测数据，e(·)表示期望，(·)^t表示转置；

对于n台发动机，计算平均协方差矩阵如下：

其中为航空发动机平均协方差矩阵，n为训练集中发动机台数，cn为第n台航空发动机的协方差矩阵；λi,i＝1,2,...,k为的第i个特征值，k表示原始监测数据的维数，为的单位特征向量矩阵，其中uj为第j个特征值对应的单位特征向量；按照特征值从大至小排序，选取r个特征值λ1≥λ2≥...≥λr,r<k记作r个主分量，则u＝[u1,u2,...,ur]^t为变换矩阵，其中r为主分量数目；原始监测数据投影到新的特征空间，在获取更低维度特征变量的同时，能够最大限度保留原始监测数据中包含的有效信息，消除噪声和不相关变量的影响。第n台航空发动机原始监测数据转换公式如下：

其中u＝[u1,u2,...,ur]^t为变换矩阵，r表示所选取主分量的数目，ur为第r个主分量对应的单位特征向量，xn为第n台航空发动机原始监测数据，xni为第n台航空发动机第i次采样的原始监测数据，为基于共同主成分分析降维后的第n台航空发动机监测数据，mn为第n台发动机的最大采样次数，为第n台航空发动机降维后第j次采样的监测数据，为第n台航空发动机降维后第mn次采样的监测数据，(·)^t表示转置。

本实施例中令r＝6，保留前6个主分量，能量所占比例达到94％以上，各主分量取值如图3所示，证明所选取的主分量个数足够保留原始监测数据中的信息。对发动机训练数据集和测试数据中的原始监测数据均进行转换。

1.2、在1.1的基础上，进行发动机健康参数的统计。研究表明发动机的前5％寿命周期可以被视作没有发生退化，故提取训练集中的未退化监测数据视作发动机的总体健康参数h＝(h1,h2,...,hn)^t，其中为第n台发动机的健康参数，为第n台航空发动机降维后第j次采样的监测数据，sn,n＝1,2,...,n表示训练集中第n台航空发动机健康参数的最大采样次数，计算如下：

sn＝[0.05mn](4)

其中sn表示训练集中第n台航空发动机健康参数的最大采样次数，mn为第n台发动机的最大采样次数，[·]表示向下取整，n为训练集中发动机台数；

1.3、获取发动机的健康数据后，首先计算航空发动机未退化监测数据均值。航空发动机未退化监测数据均值m表示如下：

其中m为航空发动机未退化监测数据均值，sn表示训练集中第n台航空发动机健康参数的最大采样次数，为第n台航空发动机降维后第j次采样的监测数据，n为训练集中发动机台数，∑表示求和；

m的物理含义是指发动机在未发生退化时的基准监测数据。发动机的健康指标可通过当前时刻监测数据与发动机未退化时基准健康数据的ed确定。每台发动机的健康指标计算公式如下：

其中tj为第n台发动机第j次采样的时间，yn(tj)为第j次采样时第n台发动机健康指标，m为航空发动机未退化监测数据均值，为第n台航空发动机降维后第j次采样的监测数据；故第n台发动机健康指标其中mn为第n台发动机的最大采样次数。

以#1、#3号训练发动机为例，图4a和图4b是基于ed的发动机健康指标曲线，观察可知发动机总体性能呈现下降趋势，在运行初期退化率较小，后期退化速度加快。由此可证明航空发动机退化轨迹带有非线性漂移。

1.4、基于发动机健康指标，确定发动机失效阈值。根据研究表明，航空发动机退化过程如图5所示，被划分为四个阶段，最后一阶段可视作发动机失效阶段。本研究基于k‐means聚类算法，聚类数目设置为4，计算最后一类的聚类中心作为发动机失效阈值ω。具体实施步骤如下：

第一步，对于第n台发动机健康指标每次采样的健康指标视作一个样本。

第二步，随机选择4个初始聚类中心z1(k),z2(k)…z4(k)，k表示迭代次数，初始值为1，每迭代一次加1；

第三步，逐个将yn(tp),p＝1,2,...,mn按最小距离准则分配到4个中心为zi(k)的类中。

第三步，分计算各类的新中心：nj即第j类中的样本个数，oj表示属于第j类的样本集合。

第四步，如果zj(k+1)≠zj(k)则转到第2步，将模式重新分类，重复迭代计算，直到聚类中心收敛，记录4个聚类中心的最大值ωmax(n)。

第五步，对于每一台发动机，重复第1、2、3、4步，选取ωmax(n)中的最小值，视作发动机失效阈值，即ω＝min(ωmax(n)),n＝1,2,...,100,其中min(·)表示取最小值。

本实施例中经计算航空发动机的失效阈值ω＝1.27。

2、航空发动机退化建模及参数估计

2.1、航空发动机的退化过程中，初期退化并不显著，后期由于损耗失效导致退化速度加快，健康指标呈现增大趋势并且整个过程不可逆。因此，选择带非线性漂移的维纳过程描述涡扇发动机的退化过程。对于假设在采样时间t，健康指标为y(t)，失效阈值为ω，基于维纳过程的航空发动机退化过程可以描述为下式：

y(t)＝y(0)+at^b+σb(t)(7)

其中，t为采样时间，非线性漂移部分为at^b，扩散系数为σ，b(t)为布朗运动；为表征制造偏差和运行环境导致发动机个体之间的差异性，a为非线性漂移部分的随机变量，满足其中n(·)表示正态分布，μa为随机变量a的均值，σa为随机变量a的标准差；同时将b定义为非线性漂移部分的常量表征发动机的相同特性；忽略发动机原始磨损，对于未运行的发动机而言，假设其初始退化状态为0，则有y(0)＝0。

发动机在某一时刻健康指标等于或者超过失效失效阈值的时候，系统必须停止运行。故航空发动机的寿命可以视作维纳过程的首次穿越失效阈值的时间，定义如下：

t＝inf{t:y(t)≥ω|y(0)<ω}(8)

其中：t为发动机寿命周期，t为采样时间，y(t)为t时刻健康指标，ω为失效阈值，inf{·}表示下确界；

2.2、基于最大似然法的航空发动机退化模型参数估计。在建立涡扇发动机的退化模型后，需要基于发动机健康指标对模型进行参数估计。每台发动机在多个采样点的健康指标服从多维正态分布，故第n台发动机的健康指标为：

其中μn为第n台发动机的健康指标均值向量，a为非线性漂移部分的随机变量，b为非线性漂移部分的常量，tj为在第j次采样的时间，e(·)表示期望，(·)^t表示转置；本实施例中tj＝j。

其中σn为第n台发动机的健康指标协方差矩阵，cov(·)表示协方差，σ为扩散系数，σa为随机变量a的标准差，b为非线性漂移部分的常量，tj为第n台发动机第j次采样的时间，(·)^t表示转置；

对于不同发动机而言，退化过程独立同分布，因此退化模型的似然函数为:

其中l(μa,σa,σ,b|y)表示关于总体发动机健康指标y的似然函数，μa为随机变量a的均值，σa为随机变量a的标准差，σ为扩散系数，b为非线性漂移部分的常量，n为训练集中发动机台数，mn为第n台发动机的最大采样次数，yn为第n台发动机的健康指标，σn为第n台发动机的健康指标协方差矩阵，μn为第n台发动机的健康指标均值向量，|·|表示取模操作，为σn的逆矩阵，exp(·)表示以e为底的指数函数，∏表示求积；

其中μa为随机变量a的均值，σa为随机变量a的标准差，σ为扩散系数，b为非线性漂移部分的常量，y为总体发动机健康指标，n为训练集中发动机台数，mn为第n台发动机的最大采样次数，σn为第n台发动机的健康指标协方差矩阵，|·|表示取模操作，为σn的逆矩阵，yn为第n台发动机的健康指标，μn为第n台发动机的健康指标均值向量；

通过最大化似然函数进行参数估计。

其中tj为第n台发动机第j次采样的时间，表示偏导数；

其中a为非线性漂移部分的随机变量，μa为随机变量a的均值，σa为随机变量a的标准差，σ为扩散系数，b为非线性漂移部分的常量，为μa的估计值，n为训练集中发动机台数，tj为第n台发动机第j次采样的时间，σn为第n台发动机的健康指标协方差矩阵，σn为第n台发动机的健康指标协方差矩阵，|·|表示取模操作，为σn的逆矩阵，yn为第n台发动机的健康指标，y为总体发动机健康指标；

基于单纯形法寻找式(15)的最小值，继而获得μa估计值。

本实施例最终参数估计结果如表1所示：

表1航空发动机退化模型参数

3、建立航空发动机剩余寿命预测模型：

3.1、基于维纳过程的航空发动机剩余寿命描述。基于发动机性能退化模型具有时间平移不变性，则退化模型可以被表示为：

其中tc为航空发动机当前运行时间，li为航空发动机剩余寿命，b(·)表示布朗运动，y(tc)为航空发动机当前健康指标，y(li+tc)为航空发动机失效时的健康指标，a为非线性漂移部分的随机变量，b为非线性漂移部分的常量，σ为扩散系数，y(li)表示发动机随航空发动机剩余寿命li退化的维纳过程，∫表示积分；可知发动机剩余寿命描述仍可表征为带非线性漂移的维纳过程；此时维纳过程首次穿越ω-y(tc)的时间即为发动机的剩余寿命。

3.2、根据3.1可知航空发动机的剩余寿命模型可用带非线性漂移的维纳过程进行描述。为估计发动机的剩余寿命，首先应将带非线性漂移的维纳过程转换为布朗运动。航空发动机剩余寿命描述转换为标准维纳过程，对于非线性扩散过程，若满足：

其中μ(y,li)表示非线性漂移部分，σ′(li,u)为扩散部分，y为健康指标，li为航空发动机剩余寿命，c1和c2为任意关于时间的函数，z为初始退化量，∫表示积分，表示偏导数；

则可经公式(19)将非线性扩散过程转换布朗运动。

其中y为航空发动机健康指标，为转换后的航空发动机健康指标，li为航空发动机剩余寿命，为转换后的剩余寿命，ki，(i＝1,2,3)为任意系数且k1>0，t0为初始时间，ti,(i＝0,1,2)为初始时间且满足ti≥0，z为初始退化量，c1和c2为任意关于时间的函数；

对于发动机剩余寿命模型而言，公式(18)中的扩散部分σ(y,li)＝σ²，漂移部分μ(y,li)＝ab(li+tc)^b-1。当航空发动机剩余寿命li＝0时，y(li)＝0，据此可知初始时间t0＝0，维纳过程初始值z＝0。因此，可得下式：

其中a为非线性漂移部分的随机变量，b为非线性漂移部分的常量，σ为扩散系数，tc为航空发动机当前运行时间，li为航空发动机剩余寿命；令k1＝1,ki＝0(i＝2,3)，tj＝0(j＝1,2)，则转换过程表示如下：

其中y为航空发动机健康指标，为转换后的航空发动机健康指标，li为航空发动机剩余寿命，为转换后的剩余寿命，a为非线性漂移部分的随机变量，b为非线性漂移部分的常量，σ为扩散系数；

转换后的失效阈值：其中为ω发动机失效阈值；

4、基于性能衰退的航空发动机剩余寿命预测：

建立航空发动机剩余寿命概率密度函数模型，在步骤1、2、3的基础上，进行实时在线寿命预测。

布朗运动首次穿过失效阈值的概率密度函数表示如下：

pb(t)(ω,t)表示布朗运动首次穿过阈值的概率密度函数，ω为失效阈值，t为采样时间；

因此航空发动机剩余寿命概率密度函数为：

其中：px(li)(ω,li)表示退化过程首次穿过失效阈值的概率密度函数，li为航空发动机剩余寿命，为转换后的剩余寿命，ω为发动机失效阈值，为转换后的失效阈值，tc为航空发动机当前运行时间，y(tc)为航空发动机当前健康指标，a为非线性漂移部分的随机变量，b为非线性漂移部分的常量，σ为扩散系数，表示偏导数；以上结果满足航空发动机寿命预测的实际使用需要。

由于非线性漂移部分的随机变量则a的概率密度函数为：

其中f(a)表示非线性漂移部分的随机变量a的概率密度函数，μa和分别为随机变量a的均值和方差；

根据全概率公式，剩余寿命概率密度函数模型可以被修正为：

其中ω为失效阈值，li为航空发动机剩余寿命，tc为航空发动机当前运行时间，y(tc)为航空发动机当前健康指标，a为非线性漂移部分的随机变量，μa为随机变量a的均值，σa为随机变量a的标准差，f(a)为随机变量a的概率密度函数，b为非线性漂移部分的常量，σ为扩散系数，exp(·)表示以e为底的指数函数；

发动机预测剩余寿命计算如下：

其中，li为航空发动机剩余寿命，表示退化过程首次穿过阈值的概率密度函数；

图6按照已运行周期大小随机选择#1，#5，#10，#26，#60五台测试发动机，绘制其剩余寿命概率密度函数并且计算出预测剩余寿命，以及真实剩余寿命的对比。

发动机剩余寿命预测准确度的评价指标包括及时预测数目、确定系数r2以及惩罚得分s。剩余寿命误差区间如图7所示，预测误差其中rul为发动机真实剩余寿命，为发动机预测剩余寿命；确定系数的计算方法如下式：

其中：ruli为第i台发动机真实剩余寿命，为第i台发动机预测剩余寿命，为全部发动机真实剩余寿命的平均值；

惩罚得分的计算方法如下式：

其中e为预测误差，为预测误差为负值的发动机数目，为预测误差为正值的发动机数目；

确定系数r越接近1表明预测模型性能越好，惩罚函数值越低说明预测模型的性能越好。

本实施例测试机中100台发动机剩余寿命频数分布及惩罚函数得分如图8和图9所示，表2为剩余寿命预测结果。

表2预测性能指标结果

通过表2中的结果可知，本发明提出的方法可以提高航空发动机剩余寿命预测的准确度，考虑不相关监测数据的影响提高模型预测性能。

本发明与现有方法的最大区别之处在于对多维监测数据进行共同主成分提取，消除对于寿命预测冗余的特征；基于多维监测数据进行融合取代单变量预测；同时，引入带非线性的维纳过程描述发动机退化率非线性的特点，得到航空发动机剩余寿命预测的概率分布，进行发动机剩余寿命点估计。实验结果验证了本方法的实用性。