无需重新排序的七点Winograd傅里叶变换器的制作方法

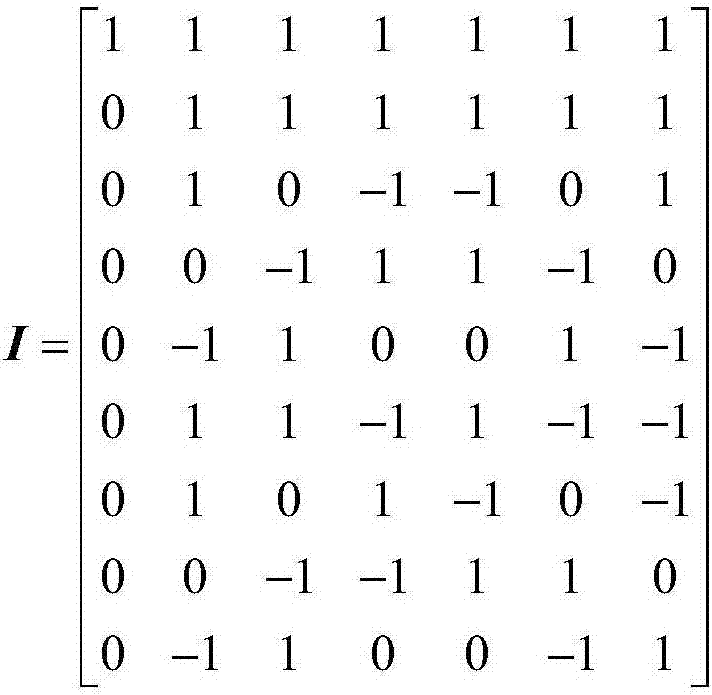
本发明涉及数字信号处理领域，特别涉及一种无需重新排序的小点数winograd快速傅里叶变换算法(winogradfouriertransformalgorithm,wfta)的实现方法。

背景技术：

随着无线通信业务的不断增长，可利用的频谱资源日益紧张。为了提高频谱利用率和通信质量，现代无线通信系统广泛采用对频率选择性衰落具有较强免疫力的正交频分复用(orthogonalfrequencyduplexmultiplexing,ofdm)技术。ofdm技术的核心是fft。fft的点数分为2的幂次和非2幂次两种。点数是2的幂次的fft算法和实现比较成熟。相比之下，非2幂次点数的fft更为灵活，近年来在drm、dtmb、lte系统中开始得到应用。因此，非2幂次点数fft的算法和实现值得深入研究。

目前，素因子算法(primefactoralgorithm,pfa)是最有效的非2幂次fft，它采用嵌套多维结构，能有效降低计算复杂度。对于n点非2幂次fft，假设n可分解为s个两两互素因子的乘积，即n＝n1n2…ns。n点pfa的基本原理是，把一维大点数fft映射成s维小点数fft，第i(i＝1,2,…,s)维fft进行n/ni次ni点小点数fft。小点数fft可借助于cooley-tukey算法、wfta以及其它高效算法。

在某些情况下，pfa需要重新排序。根据在计算过程中所处的位置，重新排序分为预扰乱和后扰乱。不考虑ni(i＝1,2,…,s)点fft的内部机制，如果第i维fft无需重新排序，那么它是同址的；否则，它是变址的，重新排序是在ni点序列内进行的，预扰乱和后扰乱分别在ni点fft之前和之后执行。类似地，不考虑每维fft的内部机制，如果n点pfa整体上无需重新排序，那么它是同序的；否则，它是变序的，重新排序是在n点序列内进行的，预扰乱和后扰乱分别在第一维fft开始前和最后一维fft结束后执行。这样，pfa理论上可分为4种：变址变序、变址同序、同址同序和同址变序。

目前，pfa要么是变址同序的，要么是同址变序的，不可避免地引入了重新排序操作。众所周知，重新排序意味着必须增加一级缓冲区，需要消耗较多的存储器资源，会增加硬件成本。此外，重新排序还会降低运算速度，增加控制的复杂度。与同址变序pfa相比，变址同序pfa消耗较少的存储器资源，两者重新排序的总延时完全相同，都是n个时钟周期，因此，变址同序pfa更可取。

技术实现要素：

针对pfa的现有实现方案中存在的需要重新排序这一技术缺点，本发明提供了无需重新排序的七点winograd傅里叶变换器。当n点非2幂次fft采用变址同序pfa实现时，如果n的某一互素因子ni＝7(i＝1,2,…,s)，那么使用本专利无需对第i维fft重新排序。

为了去除第i维7点fft的重新排序操作，需要修改常规的7点wfta。常规的7点wfta的对角矩阵是固定不变的，本发明将对角矩阵对角线上的各元素表示成角度参数θ＝2π/7*<n/7>7的函数，其中，<n/7>7表示对n/7取模7操作。对于不同的n，修改的7点wfta的对角矩阵不尽相同。

对于第i维fft，需进行n/7次无需重新排序的7点wfta，无需重新排序，简化了控制逻辑，共节约了n/7*7＝n个时钟周期，提高了运算速度，存储器消耗减少了一半，降低了硬件成本。

关于本发明的优点与精神可通过接下来的发明详述及附图得到进一步的了解。

附图说明

图1是常规的七点winograd傅里叶变换器的功能框图；

图2是输入矩阵i的具体构成；

图3是输出矩阵o的具体构成；

图4是对角矩阵d对角线上的具体构成；

图5是预扰乱的七点winograd傅里叶变换器的结构示意图；

图6是后扰乱的七点winograd傅里叶变换器的结构示意图；

图7是无需重新排序的七点winograd傅里叶变换器的功能框图；

图8是可变对角矩阵a对角线上的具体构成。

具体实施方式

下面结合附图和具体实施例对本发明作进一步说明，但不作为对本发明的限定。

n点序列x(n)的fft为

其中，n,k＝0,1,…,n-1，wn＝e-^j2π/n。直接计算n点fft的乘法和加法运算量都与n的平方成正比。当n较大时，运算量很大。

为了降低计算复杂度，当n不是2的幂次时，可采用嵌套多维的pfa实现n点fft。假设n可分解为s个两两互素因子的乘积，即n＝n1n2…ns。也就是说，任意两个因子ni和nj(i,j＝1,2,…,s，且i≠j)的最大公约数是1。注意，ni未必是素数。n点pfa的基本原理是，把一维大点数fft映射成s维fft，第i维fft进行n/ni次ni点小点数fft。小点数fft可借助于cooley-tukey算法、wfta以及其它高效算法。

为了使pfa总体上是同序的，在一维fft映射成s维fft时，根据中国余数定理，输入索引n和输出索引k采用如下相同的映射方式：

其中，符号<>n表示模n运算，ni,ki＝0,1,…,ni-1。将式(2)和(3)代入式(1)，整理可得：

其中，

对比式(2)和(3)容易发现，索引n和k的映射方式本质上完全相同。因此，只要式(4)中每维fft的索引ni和ki都是自然顺序的，n点pfa就是同序的。

在式(4)中，第i(i＝1,2,…,s)维fft的傅里叶变换因子可写作

或

式中，

众所周知，常规的ni点fft算法的输入和输出都是按照自然顺序的。如果式(4)中的第i维fft采用常规的ni点fft算法，那么式(5)是按照ni的自然顺序输入、ki′的自然顺序输出，式(6)则是按照ni′的自然顺序输入、ki的自然顺序输出。然而，由式(2)和(3)可知，同序pfa要求式(4)中的第i维fft按照ni的自然顺序输入、ki的自然顺序输出。可见，如果式(4)中的第i维fft采用常规的ni点fft算法，那么必须重新排序。具体而言，式(5)和(6)分别根据式(7)和(8)中的规则进行后扰乱和预扰乱。可见，式(4)中的第i维fft是变址的。变址通过重新排序实现。为了去掉重新排序这一额外操作，我们必须修改常规的ni点fft算法，将重新排序操作吸纳其中。

常规的ni点wfta可用向量与矩阵的连乘表示，即

v＝o*d*i*v(9)

其中，v和v分别是由ni点输入和输出序列构成的向量，i和o分别是输入和输出矩阵，d是对角矩阵。通常，矩阵i和o中的元素都只可能是0、±1和±j，与向量相乘时不涉及实质性乘法。对于对角矩阵d，除对角上的元素非零外，其它位置上的元素均为0。

当ni＝7时，n点变址同序pfa的第i维fft可采用7点wfta。图1给出了常规的七点winograd傅里叶变换器的功能框图。7点输入序列构成向量v，它先与矩阵i相乘，运算所得向量再与对角矩阵d相乘，运算所得向量最后与矩阵o相乘，运算所得向量v即为7点输出序列。图2和3分别给出了输入矩阵i和输出矩阵o的具体构成。图4给出了对角矩阵d对角线上的具体构成，从左上角到右下角的元素分别是d0～d8。

变址同序pfa第i维fft的变址是通过重新排序实现的。当ni＝7时，图5和6分别给出了预扰乱和后扰乱的七点winograd傅里叶变换器的结构示意图。为了去掉预扰乱或后扰乱中的重新排序操作，我们必须修改常规的ni＝7点wfta，将重新排序操作吸纳其中。

图7给出了无需重新排序的七点winograd傅里叶变换器的功能框图，它主要由输入矩阵i、可变对角矩阵a、输出矩阵o和复数乘法器四种功能模块组成。输出向量与输入向量满足：v＝o*a*i*v。与常规的7点wfta相比，无需重新排序的7点wfta的矩阵i和o均保持不变，对角矩阵不再是常数，其对角线上的各元素修改为角度参数θ＝2π/7*<n/7>7的函数，其中，<n/7>7表示对n/7取模7操作。图8给出了可变对角矩阵a对角线上的具体构成，从左上角到右下角的元素分别是a0～a8。对于不同的n，无需重新排序的7点wfta的对角矩阵不尽相同。

本发明提供了一种去除变址同序pfa中7点wfta重新排序的方法，当ni＝7时，n点变址同序pfa的第i维fft可通过n/7次无需重新排序的7点wfta加以实现，其步骤如下：

(1)根据n确定角度参数θ＝2π/7*<n/7>7的具体取值，在此基础上初始化可变对角矩阵a对角线上各元素的数值，使a变为常数，初始化变量l＝0(0≤l<n/7)；

(2)从输入序列x[n]中读取7个数据，它们的索引是n＝<n/7*m+7*l>n(0≤m<7)，它们构成向量v；

(3)通过复数乘法器m1，输入矩阵i与向量v相乘，得到向量p；

(4)通过复数乘法器m2，可变对角矩阵a与向量p相乘，得到向量q；

(5)通过复数乘法器m3，输出矩阵o与向量q相乘，得到向量v；

(6)将向量v中的7个数据依次写入到输出序列x[k]中，写入的索引与读取的索引完全相同，仍然是k＝<n/7*m+7*l>n；

(7)以1为步长递增改变l的取值，重复步骤(2)～(6)，直到完成n/7次无需重新排序的7点wfta。

如果n点变址同序pfa的第i维fft采用常规的7点wfta，那么每次重新排序需要7个时钟周期，这意味执行n/7次常规的7点wfta共需n/7*7＝n个时钟周期进行重新排序。可见，若n点变址同序pfa的第i维fft采用本发明，则无需重新排序，从而简化控制逻辑，可节约n个时钟周期，提高了运算速度，存储器需求可减少一半，降低了硬件成本。

以上通过具体实施方式和实施例对本发明进行了详细的说明，对于本领域的技术人员来说，在不脱离本发明原理的情况下，还可做出若干变形和改进，这些也应视为本发明的保护范围。