一种尺度参数控制可调的信号包络线提取方法与流程

本发明涉及一种信号包络线提取方法，尤其涉及一种尺度参数控制可调的信号包络线提取方法。

背景技术：

信号的包络线即是信号的外轮廓，包络线分析方法是工程信号处理中常用且有效的一种信号分析方法，尤其是在往复机械振动信号分析以及机械故障诊断分析中具有非常重要的作用。很多的工程实际信号(尤其是往复机械振动信号)波形非常复杂，多为包含多个局部冲击的非平稳信号，直接对信号分析处理的难度较大，但其包络线具有一定的规律或一定的趋势，对包络线进一步分析可以获取很多有用的信息。例如，内燃机缸盖振动信号属于典型的准周期非平稳信号，其中包含了多个局部冲击，直接对信号进行时域分析、频域分析甚至时频分析等的复杂度较大，且难以获取直观有效的规律特征，但振动信号整周期的包络线具有清晰直观的波形特征，且各周期的振动信号包络线具有显著的相似性，便于对异常振动冲击的出现和冲击特征的变化进行检测，此外通过对包络线进一步分析可以有效获取各个冲击出现的相位和冲击的能量。

描绘出合适的包络线是进行包络分析的关键所在，也是保证包络分析有效性的前提条件。其难点在于如何通过算法实现自动描绘出符合工程信号处理需要的包络线，且能够通过少量的参数控制包络线特性，如本方法中仅通过一个参数控制包络线的平滑程度等特性。

目前对信号包络线提取的方法主要包括两大类：一类是直接提取原始信号的特征点，再通过插值方法将特征点连接起来构成包络线，如emd分解中采用的利用一阶极值点求取信号包络线的方法，即提取信号中的极大(小)值点后通过三次样条插值的方法求取信号的上(下)包络线，此外也包络二阶极值或多阶极值作为特征点，并通过其它各类插值方法进行连线的方法。二类是通过解调的方法将信号中的低频信号分离出来作为原始信号的包络线，如hilbert变换和小波变换进行包络解调求取低频包络线的方法。上述两类方法中，第一类较为简单直接，计算量小，对各类信号的适应性也很强，但经常出现包络线光滑性不好(如存在“折点”)或紧密贴合性不好(如“过冲”失真)等显著缺陷问题，更重要的是在出现上述问题后，现有传统方法难以在不改变包络算法的情况下仅通过控制某一参数来达到连续调整包络线性能的目的。而第二类方法中，直接用hilbert变换提取的机械冲击信号的包络往往不够光滑，存在的毛刺很多，含有大量的高频分量；而小波变换求包络的方法虽然可以通过调整尺度参数获得不同光滑程度的包络线，但具有确切表达式的基函数导致其自适应能力较差，使得对任意非平稳、非线性信号的处理能力有限；此外，第二类方法的计算较为复杂，计算量较大，在一些数据量大且要求实时多次计算或循环计算包络线的场合难以得到有效应用。

本发明充分分析了现有传统方法求取包络线的优缺点，提出一种尺度参数控制可调的信号包络线提取方法，该方法同时兼顾了上述两类方法的优点，其本质上属于上述第一类方法，但同时具备可通过调整尺度参数来达到连续控制包络线光滑性的能力。

技术实现要素：

本发明的目的在于针对现有传统的信号包络线提取方法存在的缺点和不足，提供一种简单有效的尺度参数控制可调的信号包络线提取方法。这种方法不仅计算简单、适应性强，并且具备仅调整单个尺度参数即可连续控制包络线光滑性的能力。

本发明的目的通过以下技术方案实现(以上包络线为例，下包络线同理)：本发明首先提取原信号中的极大值点(一阶极大值点或多阶极大值点)构成一组特征点；然后求取该组特征点的极小值，并计算每个极小值点处的某一个或多个特征值，若该特征值满足预设条件则将其从该组特征点中剔除，得到新的特征点序列；再对新的特征点序列重复上一步骤，循环剔除部分特征点，直到连续两次循环得到的特征点个数只差不大于1(或其它正整数)；最后将最终得到的特征点序列通过插值的方法连接起来，得到信号的上包络线。其中，特征点的剔除条件由尺度参数控制，从而达到调整单一参数即可连续控制包络线光滑性的目的。

1、一种尺度参数控制可调的信号包络线提取方法，其特征在于包括以下步骤：

(1)提取原信号中的极大值点，构成一组特征点序列；

(2)提取上述特征点序列中所有极小值点，计算上述每个极小值点处的特征值；并将上述特征值满足给定条件的极小值点从上述特征点序列中剔除，形成新的上述特征点序列；

(3)在上述新的特征点序列中再次寻找极小值点，剔除上述特征值满足设定条件的极小值点；循环剔除上述特征点序列中的部分点，直到满足循环终止条件，得到最终的特征点序列；

(4)将最终得到的上述新特征点序列在原始信号中进行插值，将上述特征点序列和插值点连线得到上包络线。

或者

(1)提取原信号中的极小值点，构成一组特征点序列；

(2)提取上述特征点序列中所有极大值点，计算上述每个极大值点处的特征值；并将上述特征值满足给定条件的极大值点从上述特征点序列中剔除，形成新的上述特征点序列；

(3)在上述新的特征点序列中再次寻找极大值点，剔除上述特征值满足设定条件的极大值点；循环剔除上述特征点序列中的部分点，直到满足循环终止条件，得到最终的特征点序列；

(4)将最终得到的上述新特征点序列在原始信号中进行插值，将上述特征点序列和插值点连线得到下包络线。

步骤(2)中的特征值char(a)(k)的计算公式为：

char(a)(k)＝c(a)(k)-d(a)(k)

其中，c(a)(k)表示在横坐标伸缩尺度为a的情况下，三个点通过三点作圆求得的圆心纵坐标，上述三个点为：上述步骤(2)极值点及该极值在步骤(1)所述特征点序列中前后相邻的两个点。d(a)(k)表示在横坐标伸缩尺度为a的情况下，上述步骤(2)极值点在步骤(1)所述特征点序列前后两点的连线在上述极值点处的线性插值。

且特征值char(a)(k)不大于0。

步骤(3)中的循环终止条件为：连续两次形成的新特征点序列的长度之差不大于给定个数n_stop。n_stop一般取1-10之间的正整数，包括1-10。

以下对本发明作进一步的说明，包括如下步骤(仍以上包络线为例，下包络线同理)：

第一步，提取原信号s(i)中的极大值点(一阶极大值点或多阶极大值点)，构成一组特征点序列y1(j)，并记录其在原信号中的位置序列x1(j)；

第二步，计算y1(j)的极小值序列y2(k)，并记录其在x1(j)中的位置序列x2(k),则其在原信号s(i)中的位置序列x1(x2(k))，计算点(x1(x2(k)),y2(k))处的特征值char(a)(k)：

char(a)(k)＝c(a)(k)-d(a)(k)(1)

其中c(a)(k)表示点(x2(k),y2(k))及其在(x1(j),y1(j))序列中与其相邻的前后两点，在横坐标伸缩比例为a的情况下，通过三点作圆求得的圆心纵坐标；d(a)(k)表示在横坐标伸缩比例为a的情况下，以特征点在原信号s(i)的位置序列作为横坐标，点(x2(k),y2(k))在(x1(j),y1(j))序列中与其相邻的前后两点连线在x1(x2(k))处的线性插值。

若char(a)(k)<0，则将该点(x2(k),y2(k))从(x1(j),y1(j))序列中剔除。

此处为给出c(a)(k)和d(a)(k)的表达式及其随横轴伸缩系数a的变化规律，给出以下计算过程：

设平面中三点坐标分别是(x1,y1)、(x2,y2)、(x3,y3),其中x1<x2<x3，y1>y2,y2<y3，此三点确定的圆心坐标为(xc,yc)；(x1,y1)、(x3,y3)两点连线在x2处的线性插值为yi，则：

取：

x1＝x1-x2，x3＝x3-x2，xc＝xc-x2；y1＝y1-y2，y3＝y3-y2，yc＝yc-y2；(4)

则：

x1<0，x3>0；y1>0，y3>0；(5)

将(4)中各式带入(2)中，得：

由(5)可知：

yc>0

(8)

若令x′＝a·x(a>0)，则得到新的圆心纵坐标yc′及插值点纵坐标yi′:

yi′＝yi

(10)

由(5)得：

因此：a＝1时，yc′＝yc>0；

a>1时，yc′>yc>0；

0<a<1时，0<yc′<yc；

根据以上计算可知：一方面，可以通过调节尺度参数a(a>0)的方法来调整三点作圆的圆心位置，并且当尺度参数a大于1时,随着a的增大，圆心位置提高；当尺度参数a小于1时,随着尺度参数a的减小，圆心位置下降。另一方面，插值点的纵坐标不会随着尺度参数a的变化而变化，因此插值点可以作为不动的参考点。

为便于后续分析，此处需要证明：无论a(a>0)取何值，存在yc′始终大于yi。

由公式(9)中yc′的表达式可知，虽然a＝0的情况在公式推导的过程中会导致推导过程中某些式子的分母为零，但最终结果均能够将a从分母中约掉，又由于在题设情况下，yc′是a的增函数，所以可在yc′中直接令a＝0获得趋近于零时的yc′的最小值。

将a＝0带入公式(9)，并将yc′与yi相减可得：

由公式(5)可知：公式(11)等号右边的分母始终小于零，若要证明存在yc'>yi恒成立，则只需证明存在(x1,y1)和(x2，y2)，使得(x1y3²+x3y1²)(x3+x1)-4x1x3y1y3<0即可。

根据(5)可设：x1＝-αx3；y1＝βy3，其中α>0，β>0，由于在随机信号中，x1，y1，x2，y2是四个独立的变量，则α，β可以取任意正实数。则公式(11)等号右边分子部分可化简为：

则容易看出在α介于β²与1之间，并且β足够小(趋于0)(例如：β＝0.1，α＝0.5)或β足够大(趋于正无穷)(例如β＝10，α＝5)时，式(12)均可以小于0。综上可知，存在(x1,y1)、(x2,y2)、(x3,y3)(x1<x2<x3，y1>y2,y2<y3)使得无论缩放系数a如何变化，yc>yi恒成立。

基于以上计算过程，并且为便于计算，令：

x1(x2(k)-1)＝x1(x2(k)-1)-x1(x2(k))

x1(x2(k)+1)＝x1(x2(k)+1)-x1(x2(k))

y1(x2(k)-1)＝y1(x2(k)-1)-y1(x2(k))

y1(x2(k)+1)＝y1(x2(k)+1)-y1(x2(k))

可以得到ca(k)和da(k)的表达式：

第三步，将序列y1(j)中满足式(1)条件的特征点剔除后，形成新的一组序列，并重复第二步，循环剔除满足条件的点，直到连续两次剔除的点数不大于n_stop。

第四步，将经上述第二步和第三步骤后仍保留下来的点，用插值的方法连接起来，作为信号的上包络线。

本发明中，ca(k)是尺度参数a(a>0)的函数，da(k)与a无关。可以通过调整尺度参数控制信号中某些特征点是否被剔除，当a增大时，则ca(k)增大，被踢出的特征点数量减少，得到的曲线更不平滑(即更接近极值点包络线)；当a减小时，则ca(k)减小，被踢出的特征点数量增加，得到的曲线更平滑，并且存在永远无法剔除的特征点，即通过改变尺度参数a得到的一族包络线中存在“最光滑”包络线的极限情况。同时，同一参数a保证了在整个信号长度范围内，信号在同一尺度下进行包络提取。

附图说明

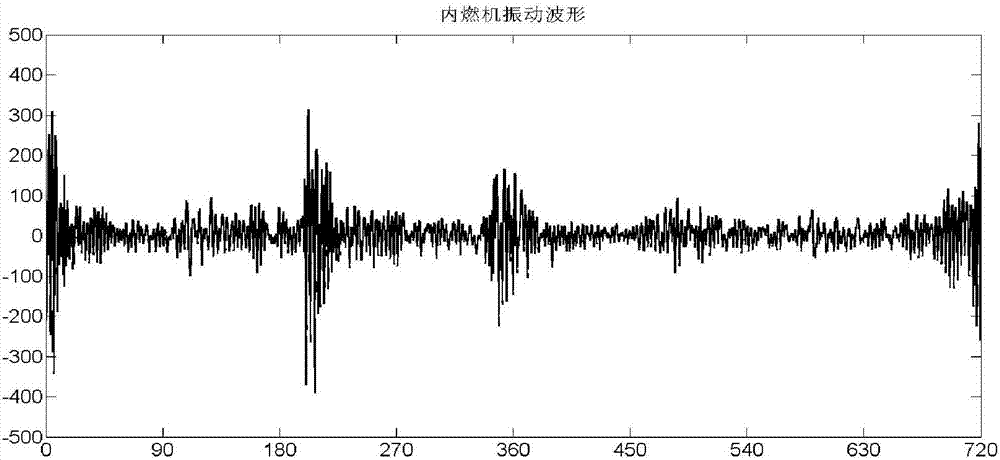
图1内燃机振动原始波形

图2a本发明中尺度参数为10的包络线

图2b本发明中尺度参数为10的包络线细化波形

图3a本发明中尺度参数为1的包络线

图3b本发明中尺度参数为1的包络线细化波形

图4a本发明中尺度参数为0.1的包络线

图4b本发明中尺度参数为0.1的包络线细化波形

图5a本发明中尺度参数为0的包络线及其细化波形

图5b本发明中尺度参数为0的包络线细化波形

图6a一阶极值包络线

图6b一阶极值包络线细化波形

图7ahilbert变换所求包络线

图7bhilbert变换所求包络线的细化波形

具体实施方式

为了更好地了解本发明的技术方案，以下结合附图对本发明的具体实施方式作进一步的详细说明。

第一步，内燃机缸盖振动整周期信号s(i)，如图1所示，提取s(i)的极大(小)值点，构成一组特征点序列y1(j)，并记录其在原信号s(i)中的位置序列x1(j)；

第二步，计算y1(j)的极小(大)值序列y2(k)，并记录其在x1(j)中的位置序列x2(k)，则其在原信号s(i)中的位置序列x1(x2(k))，计算点(x1(x2(k)),y2(k))处的特征值char(a)(k)，

char(a)(k)＝c(a)(k)-d(a)(k)

其中：

x1(x2(k)-1)＝x1(x2(k)-1)-x1(x2(k))

x1(x2(k)+1)＝x1(x2(k)+1)-x1(x2(k))

y1(x2(k)-1)＝y1(x2(k)-1)-y1(x2(k))

y1(x2(k)+1)＝y1(x2(k)+1)-y1(x2(k))

若满足char(a)(k)<0条件，则将该点(x2(k),y2(k))从(x1(j),y1(j))序列中剔除，形成新的上述特征点序列；

第三步，将上述第二步得到的新的特征点序列中再次寻找极小(大)值点，剔除上述特征值满足设定条件的极小(大)值点，再次形成新的特征点序列，循环剔除满足char(a)(k)<0条件的点，直到连续两次形成的新特征点序列的长度之差不大于给定个数n_stop。

第四步，将经上述第(2)步和第(3)步骤后仍保留下来的点，用插值的方法连接起来，作为信号的上(下)包络线。

分别将尺度参数设置为a＝10，a＝1，a＝0.1，a＝0，得到四种包络线的波形，如图2-图5所示；此外，图6为利用一阶极值求包络的方法求得的包络线，图7为hilbert变换求包络的方法求得的包络线，容易看出：与传统的求包络线的方法相比本发明的包络线提取方法简洁灵活，可根据求取包络线的目的及平滑性要求，仅通过修改单一的尺度参数就可以控制包络线的平滑性。