一种快速定位图像中合适矩形背景区域的方法与流程

本发明属于计算机图像处理领域，尤其涉及一种能快速定位图像中一块用于嵌入新图像的合适的矩形背景区域的方法。

背景技术：

科技的发展促进了数字图像的广泛应用，现在已经可以很方便的获取数字图像，并在图像中嵌入新的图像，如二维码等，从而完成对数字图像的修改。然而，要想使嵌入的新的图像信息能够不掩盖图像载体本身包含的重要信息，就需要一种方法来定位载体本身的背景区域，并在背景区域中选择一块合适的区域，用于嵌入新的图像信息。

目前，数字图像中背景区域的定位研究仍处于初期阶段，大部分的研究工作是数字图像中的物体检测，并且在这方面取得了巨大的进步。1998年itti提出了一种经典的显著图(saliencymap)的方法，主要思想就是根据图像底层的视觉信息，给出图像的视觉显著区域。也有专家提出了一种物体检测的分割图算法(sm)，sm是研究如何给任意形状的物体定位，并且使用紧致的边界将物体标定出来。传统的物体定位方法是滑动窗口搜索方法(slidingwindowsearch)，是使用固定大小的窗口在图片上均匀的滑动，通过每个位置时，将此时窗口内的特征代入实现训练的分类器中进行测试，在整个过程中与分类器最高响应的那个窗口位置则被视为物体的位置。以上均是图像中物体的检测方法，我们需要根据检测到的物体区域再去定位背景区域，最后虽然实现了背景区域的定位，但找到的背景区域仍然是分散分布于原载体图像中，而不是一块已经确定了位置的合适的区域，要想实现合适位置的定位，还需要继续对分散的图片背景区域进行定位处理，提高了工作的复杂度，同时大大降低了我们工作的速度以及服务的效率与质量。

技术实现要素：

本发明的目的在于提出一种快速定位图像中一块合适的矩形背景区域的方法，从而能够将新的图像信息，如二维码，嵌入原载体图片的合适位置，而不掩盖原图片包含的重要信息。本发明定位速度快，定位准确率高，解决了一直以来只能在嵌入新图象与破坏原始图像完整性中选择其一的问题。

为实现上述目的，本发明采用如下的技术方案：

一种快速定位图像中合适矩形背景区域方法，包括以下步骤：

步骤一、读入数字图像，并将数字图像转换成二值图像；

步骤二、使用图像分割的方法，在分割窗口(第一次将原始图像作为分割窗口)大于等于嵌入图像大小的前提条件下，对图像进行循环的分割，取分割窗口中包含白点最少的区域作为新的分割窗口继续分割，直到得到的分割窗口包含的白点数最少且不能再继续分割(此时，载入图像的长宽的2倍都分别大于分割窗口的长宽)，此时定位该分割窗口；

步骤三：在步骤二中定位到的分割窗口中使用嵌入图像大小的矩形窗口作为滑动窗口进行滑动窗口搜索，直到某一位置的白点数为0就将该区域作为最终的区域，或者没有白点数为0的区域，就将白点数最少的区域作为最后的区域，如此就找到了合适的新图象嵌入区域。

作为优选，步骤一具体包括：

步骤1.1、把数字图像转换成灰度级图像；

步骤1.2、二值化处理，对灰度级图像进行边缘检测，如使用sobel边缘检测器进行边缘检测，来将灰度级图像i转化为二值图像bw，检测到边缘的位置其值为对应于白色的值“1”，其他位置其值为对应于黑色的值“0”。

作为优选，用于定位图像中一块刚好适合嵌入新图像并且大小大于等于要嵌入图像大小的合适的矩形区域的位置的步骤二包括，首先要对图像步骤一中得到的二值图像进行形态学中的膨胀运算，使得图像中目标增大，填充图像中细小的空洞，并平滑连通物体的边界，使边界向外扩张；其次，就是使用图像分割的方法来定位图像中一块合适的矩形背景区域，其具体步骤如下2.1-2.5：

步骤2.1.首先判断原始载体图像bw(记作b)的大小[mn](其中bw的左上角坐标为(x,y))以及要嵌入的图像的大小[hw],只要满足条件h<m和w<n，就执行如下步骤；

步骤2.2.如果2*h>m，2*w<＝n，将经步骤一处理后的原始图像按水平方向分割为b1，b2，b3三部分，其中，

b1＝bw(x:x+m-1,y:y+n/2-1)；

b2＝bw(x:x+m-1,y+n/2-1:y+n-1)；

b3＝bw(x:x+m-1,y+n/4-1:y+3*n/4-1)；

计算b1，b2，b3中白点最少的区域，记作b，若b是b1，则x，y不变；若b是b2，则x不变，y＝n/2+y-1；若b是b3，则x不变，y＝n/3+y-1；同时，m，n变为b的大小。只要满足h<m和w<n就执行如下步骤；

步骤2.3.如果2*h<m，2*w<＝n，将经步骤一处理后的原始图像

分割为b1，b2，b3，b4，b5五部分，其中，

b1＝bw(x:x+m/2-1,y:y+n/2-1)；

b2＝bw(x:x+m/2-1,y+n/2-1:y+n-1)；

b3＝bw(x+m/2-1:x+m-1,y:y+n/2-1)；

b4＝bw(x+m/2-1:x+m-1:y+n/2-1:y+n-1)；

b5＝bw(x+m/4-1:x+3*m/4-1,y+n/4-1:y+3*n/4-1)；

计算b1，b2，b3，b4，b5中白点最少的区域，记作b，若b是b1，则x，y不变；若b是b2，则x不变，y＝n/2+y-1；若b是b3，则y不变，x＝x+m/2-1；若b是b4，则x＝x+m/2-1，y＝y+n/2-1；若b是b5，则x＝x+m/3-1，y＝y+n/3-1；同时，m，n变为b的大小。只要满足h<m和w<n，就执行如下步骤；

步骤2.4.如果2*h<m，2*w>n，将经步骤一处理后的原始图像按

垂直方向分割为b1，b2，b3三部分，其中，

b1＝bw(x:x+m/2-1,y:y+n-1)；

b2＝bw(x+m/2-1:x+m-1,y:y+n-1)；

b3＝bw(x+m/4-1:x+3*m/4-1,y:y+n-1)；

计算b1，b2，b3中白点最少的区域b，若b是b1，则x，y不变；若b是b2，则y不变，x＝x+m/2-1；若b是b3，则y不变，x＝x+m/3-1；同时，m，n变为b的大小。只要满足h<m和w<n，就执行如下步骤；

步骤2.5.如果2*h>m，2*w>n，则b就是最后定位到的不可分割的分割窗口图像。

作为优选，步骤三具体为：对步骤二中得到的最小的不可分割的分割窗口图像，计算该图像中大小为[hw](嵌入图像的大小)的正中间的图像中白点的数目，如果该数目为0，则该窗口就作为最后找到的矩形窗口；如果不为0，那么再计算该图像中大小为[hw]的上中、下中、左中、右中、左上角、右上角、左下角、右下角8个子窗口中的白点的数目，如果有一个白点数目为0，那么就将该窗口作为最后找到的矩形窗口；如果都不为0，那么就使用一个大小为[hw]的矩形区域作为滑动窗口，对步骤二中得到的最小的不可分割图像进行滑动，得到某一个区域位置，该区域白点数目为0或最少，将该区域作为最后找到的合适的背景区域；其中，该步骤中先计算正中间以及上中、下中、左中、右中、左上角、右上角、左下角、右下角9个子窗口的区域中白点的数目，有利于找到背景中位置合适的区域，且能提高效率。

附图说明

根据下面通过示例并参照附图对本发明具体实施例的描述，将显现出本发明的其他特征和优点，在附图中：

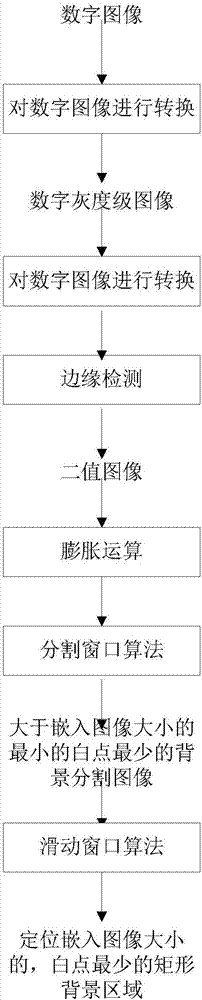
图1是本发明的用于定位图像中一块合适矩形背景区域的方法的主要步骤的流程图。

图2是窗口分割图算法流程图；

图3是图像水平分割方式的示意图；

图4是图像垂直分割方式的示意图；

图5是图像水平垂直分割方式的示意图；

图6a为计算子窗口的正中间区域的白点数目的示意图；

图6b为计算子窗口的上中区域的白点数目的示意图；

图6c为计算子窗口的下中区域的白点数目的示意图；

图6d为计算子窗口的左中区域的白点数目的示意图；

图6e为计算子窗口的右中区域的白点数目的示意图；

图6f为计算子窗口的左上角间区域的白点数目的示意图；

图6g为计算子窗口的右上角区域的白点数目的示意图；

图6h为计算子窗口的左下角区域的白点数目的示意图；

图6i为计算子窗口的右下角区域的白点数目的示意图；

图7是滑动窗口算法的流程图；

图8a是本发明的应用实施例的原始图像；

图8b是本发明的应用实施例的灰度图像；

图8c是本发明的应用实施例的二值图像；

图8d是本发明的应用实施例的膨胀处理后图像；

图8e是以滑动窗口为[200,200]的找到最小子窗口的示意图；

图8f是以滑动窗口为[200,200]找到区域的示意图；

图8g是以滑动窗口为[220,220]的找到最小子窗口的示意图；

图8h是以滑动窗口为[220,220]找到区域的示意图；

图8i是以滑动窗口为[250,250]的找到最小子窗口的示意图；

图8j是以滑动窗口为[250,250]找到区域的示意图；

图8k是显示将新的二维码图像(大小分别为[200,200])嵌入原始图像找到的区域中的最终效果图；

图8l是显示了将新的二维码图像(大小分别为[220,220])嵌入原始图像找到的区域中的最终效果图；

图8m是显示了将新的二维码图像(大小分别为[250,250])嵌入原始图像找到的区域中的最终效果图。

具体实施方式

为了使本发明的目的、技术方案及优点更加清晰，下面将结合附图就实施例，对本发明进行进一步的详细说明。应当理解，此处所描述的具体实施例仅仅用以解释本发明，并不用于限定本发明。

图1是本发明的用于定位图像中一块合适矩形背景区域的方法的主要步骤的流程图。如图所示，先读入数字图像，并将数字图像转换成灰度级图像，再使用边缘检测器将其转换成二值图像，然后对该图像进行膨胀处理；接着使用图像分割的方法，定位图像中一块刚好适合嵌入新图像并且大小大于等于要嵌入图像大小的合适的矩形区域的位置；最后在上面找到的矩形背景区域中使用滑动窗口搜索的方法，找到合适的新图象嵌入区域。

图2给出图像窗口分割算法。该算法第一步是计算原始图像bw(记作b)大小为[mn]，左上角坐标为(x,y)，嵌入图像大小为[hw]；第二步，比较原始图像和嵌入图像的长宽(这里有一个初始条件，即最后得到的分割窗口的大小必须大于等于嵌入图像的大小，因此以下要进行的所有的判断首先应基于这个条件)，即判断h<m&&w<n是否成立，若h<m&&w<n不成立，算法结束，找到的最小分割窗口就是b,反之，进行第三步，第三步主要包括以下几种判断：(1)若2h>m，2w<＝n成立，就进行图3所示的水平分割，分为三部分，每部分均为b的1/2(长度仍为h,宽度为w的1/2)，通过计算，得到三部分中白点数最少的那一部分，记作b，并重新计算b的大小为[mn]及其左上角坐标，然后再返回第二步继续判断。(2)若2h<＝m,2w>n,则进行图4所示的垂直分割，分为三部分，每部分为b的1/2(长度为h的1/2,宽度不变)，通过计算，得到三部分中白点数最少的那一部分，记作b，并重新计算b的大小为[mn]及其左上角坐标，然后再返回第二步继续判断。(3)若2h<＝m,2w<＝n,则进行图5所示的垂直水平分割，分为五部分，每一部分均为原始图片的1/4(长宽均为原图的1/2),通过计算，得到五部分中白点数最少的那一部分，记作b，并重新计算b的大小为[mn]及其左上角坐标，然后再返回第二步继续判断。(4)若2h>m,2w>n,则分割结束，b就是最小的分割窗口。通过以上三步的图像分割方法，得到可以嵌入新图象的最小的子窗口。

图6a—图6i是进行滑动窗口方法前，对图2中得到的最小子窗口b，先计算该子窗口的正中间以及上中、下中、左中、右中、左上角、右上角、左下角、右下角9个区域中(大小为[hw])白点的数目，如果这9个区域中有白点数目为0的区域，就以该区域作为最终的区域，不用再进行滑动窗口算法，这有利于找到背景中位置较合适的区域，且大大提高了效率。

图7是滑动窗口算法，对分割方法得到的最小子窗口(大小为[mn]；左上角坐标为(x,y))用一个大小为[hw]的滑动窗口由左到右由上到下进行滑动，找到白点为0或白点最少的滑动窗口区域作为最终的区域。

图8a至图8m是本发明的应用实施例。

如图8a至图8d所示，先读入数字图像(大小[mn]为[950775],坐标(x,y)为(1,1))，接着将数字图像转换成灰度级图像，再使用边缘检测器将其转换成二值图像，然后对该图像进行膨胀处理。

如图8e、图8f所示，先使用图像分割算法找到最小子窗口，接着计算该子窗口中的正中间以及上中、下中、左中、右中、左上角、右上角、左下角、右下角9个区域中(大小[hw]为[200200])白点的数目，发现该子窗口的左中间区域中白点数目为0，因此就将该区域作为最终区域，此时程序就结束。

如图8g、图8h所示，先使用图像分割算法找到最小子窗口，接着计算该子窗口中的正中间以及上中、下中、左中、右中、左上角、右上角、左下角、右下角9个区域中(大小[hw]为[220220])白点的数目，发现该子窗口的9个区域中白点数目均不为0，因此就在该子窗口上使用滑动窗口(大小[hw]为[220220])算法进行滑动，找到了该子窗口中白点数目为0的区域，就将该区域作为最终区域，此时程序就结束。

如图8i、图8j所示，先使用图像分割算法找到最小子窗口，接着计算该子窗口中的正中间以及上中、下中、左中、右中、左上角、右上角、左下角、右下角9个区域中(大小[hw]为[250250])白点的数目，发现该子窗口的9个区域中白点数目均不为0，因此就在该子窗口上使用滑动窗口(大小[hw]为[250250])算法进行滑动，滑动完毕，发现该子窗口中没有白点数目为0的区域，因此就将白点数最少的区域作为最终区域，此时程序就结束。

如图8k、图8l、图8m所示，显示了将新的二维码图像(大小分别为[200200]、[220220]、[250250])嵌入原始图像找到的区域中的最终效果图。

本发明还有与上述流程基本相似的应用，在此不再一一举例。本发明的优点是通过图像分割算法能更好的得到位置位于中间白点数最少的背景区域，接着通过计算得到的分割窗口的正中间以及上中、下中、左中、右中、左上角、右上角、左下角、右下角9个区域中(大小为[hw])白点的数目，如果这9个区域中有白点数目为0的区域，就以该区域作为最终的区域，不用再进行滑动窗口算法，这有利于找到背景中位置较合适的区域，且大大提高了效率。最后使用滑动窗口算法能够得到合适的矩形背景区域。

本发明还可以有其他多种实施例，在不背离本发明精神及其实质的情况下，熟悉本领域的技术人员可根据本发明做出各种相应的改变和变形，但这些相应的改变和变形都应属于本发明所负担权利要求的保护范围。