基于局部高斯分布拟合与局部符号差能量驱动的活动轮廓模型图像分割方法与流程

本发明属于图像处理技术领域，涉及一种活动轮廓模型图像分割方法，特别是一种基于局部高斯分布拟合与局部符号差能量驱动的活动轮廓模型图像分割方法。

背景技术：

随着计算机科学技术的迅速发展，图像分割作为图像处理和计算机视觉、目标跟踪、以及医疗成像等领域的一项基础性课题，有着很高的应用和研究价值。在过去的几十年里，研究人员已经做出很大的努力来解决图像的分割问题，并提出了很多分割算法，其中活动轮廓模型已经成为目前该领域中较为活跃的方法之一。

用曲线演化理论和水平集方法表达的活动轮廓模型，通常可分为两种类型：基于边缘的模型和基于区域的模型。基于边缘的模型利用图像的梯度特性来构造边缘指示函数，使得演化曲线不断地向着目标的边界运动，对于梯度变化比较明显的图像有较好的分割效果。然而，对于某些包含大量噪声的目标图像往往会造成分割结果的不理想。相反，基于区域的模型被不断地开发并应用到图像分割领域，通过使用全局或局部图像信息来引导水平集演化，使得模型在应对弱边缘与不连续边界等问题时，具有更好的通用性。其中，chan和vese提出的c-v模型最具有代表性，通过假定带分割图像在同质区域内灰度的分布是均匀的，该模型具有较好的全局优化特性，且对初始轮廓曲线的依赖性很小。但是该方法在进行灰度不均匀及噪声图像的处理时，很容易出现误分割，这就限制了它的实际应用。针对上述问题，vese等人提出了ps(piecewisesmooth)模型，有效地解决了灰度不均匀图像的分割问题，但模型的计算量比较大。

为此，li等人提出了著名的lbf模型，通过将c-v模型中的全局拟合能量替代为局部二值拟合能量，该方法能很好地处理灰度不均匀图像，且具有更好的分割定位能力。但是，lbf模型对图像噪声和初始轮廓曲线比较敏感，且能量方程容易陷入局部极小。

技术实现要素：

本发明的目的是针对现有的技术存在上述问题，提出了一种基于局部高斯分布拟合与局部符号差能量驱动的活动轮廓模型图像分割方法，本活动轮廓模型图像分割方法可以实现灰度不均匀目标的分割，对初始轮廓曲线的形状、大小、位置更不敏感，且具有一定的抗噪性。

本发明的目的可通过下列技术方案来实现：

一种基于局部高斯分布拟合与局部符号差能量驱动的活动轮廓模型图像分割方法，其特征在于，该方法包括如下步骤：

s1：输入原始图像i(x)；

s2：计算图像的局部熵，进而得到图像的局部符号差能量项；

s3：初始化水平集函数φ＝φ⁰(x)，它的符号距离函数定义如下：

s4：初始化系数α、β、λ1、λ2、μ、ν、ε、σ、δt；

s5：计算局部拟合能量项e1、e2；

s6：更新水平集函数φ；

s7：判断水平集演化曲线是否满足收敛准则，若没有，转到步骤s5继续计算，直到满足终止条件。

在上述基于局部高斯分布拟合与局部符号差能量驱动的活动轮廓模型图像分割方法，在步骤s2中，图像局部熵的表达式为：

公式中，ωx是以x为中心的邻域，y是邻域中的像素，p(y,ωx)是邻域像素灰度级的分布函数，可以表示为：

图像的局部符号差能量项的表达式为：

公式中，er(x)＝e(x,b(x,r))是以x为中心的邻域像素点的局部熵，b(x,r)＝{y:|x-y|≤r,r＞0}是窗口函数；

w(x)是权重函数，定义如下：

w(x)＝∫inside(c)kσ(x-y)dy∫outside(c)kσ(x-y)dy

前景聚类f1和背景聚类f2的符号差能量e^lsd(x)定义如下：

e^lsd(x)＝f1(x)-f2(x)。

在上述基于局部高斯分布拟合与局部符号差能量驱动的活动轮廓模型图像分割方法，在步骤s5中，包括如下子步骤：

s5.1：在局部高斯分布拟合能量的基础上引入局部符号差能量项

公式中，e^lgdf、e^l分别为局部高斯分布拟合能量项和局部符号差能量项，α、β分别为lgdf项和lsd项的权重系数，其中，lgdf模型的能量泛函如下所示：

s5.2：为了保持演化曲线本身的光滑度和规则性，并且尽可能减少在分割结果中出现孤立和较小的区域，需要在目标函数中引入长度项和惩罚项，则模型的能量泛函可以表示为：

公式中，l(φ)和p(φ)分别为长度项和惩罚项，ν和μ分别是它们的权重系数；

s5.3：引入heaviside函数h(z)和dirac函数δ(z)，则能量泛函可以表示为如下的水平集形式：

公式中，m1,ε(φ(y))＝hε(φ(y))；m2,ε(φ(y))＝1-hε(φ(y)),在实际过程中，heaviside函数近似为一个光滑函数hε(z)：

dirac函数δ(z)相应的正则化形式δε(z)定义如下：

s5.4：采用标准的梯度下降流法来极小化能量泛函,固定水平集函数φ，对s5.3中的水平集形式关于函数u1、u2、σ1、σ2极小化泛函f(φ)，通过变分法可得：

s5.5：固定u1、u2、σ1和σ2来最小化s5.3中的水平集形式所描述的能量泛函f(φ)，同时引入时间变量t，可得到如下的水平集演化方程：

公式中，

与现有技术相比，本基于局部高斯分布拟合与局部符号差能量驱动的活动轮廓模型图像分割方法具有以下优点：

首先，以引入图像局部熵的局部符号差(localsigneddifference，lsd)能量项和局部高斯分布拟合(localgaussiandistributionfitting，lgdf)能量项的线性组合来构造水平集函数的演化力；然后，运用水平集方法求解该能量方程，从而驱使活动轮廓向目标的边缘演化。实验结果表明，本发明所提出的方法可以实现灰度不均匀目标的分割，对初始轮廓曲线的形状、大小、位置更不敏感，且具有一定的抗噪性。

附图说明

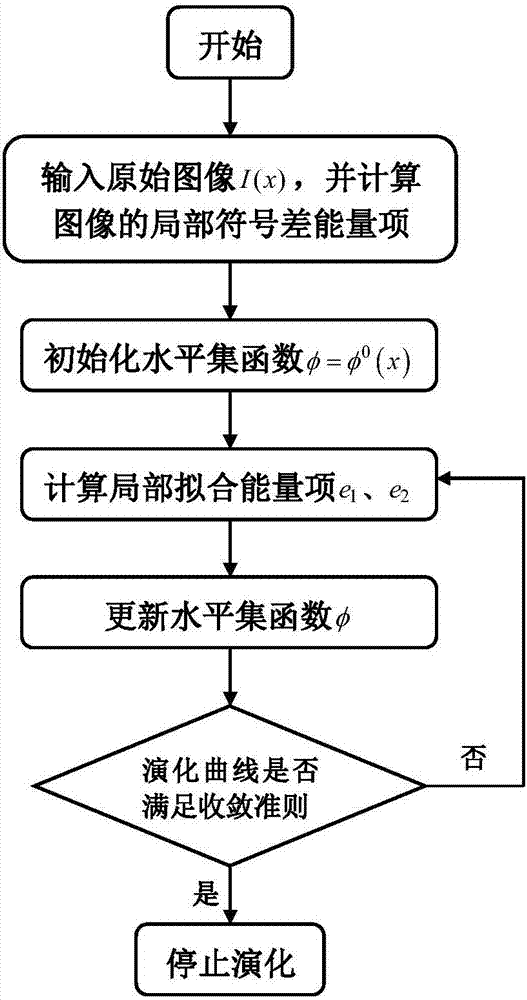
图1为本发明所涉及方法的流程框图。

图2为图像的局部熵显示图。

图3为各算法对合成噪声图像的分割结果，其中，(a)为lbf模型的分割结果；(b)为lgdf模型的分割结果；(c)为lrs模型的分割结果；(d)为lgif模型的分割结果；(e)为glgdf模型的分割结果；(f)为本发明所提方法的分割结果。

图4为各算法对t型图像的分割结果，其中，(a)为lbf模型的分割结果；(b)为lgdf模型的分割结果；(c)为lrs模型的分割结果；(d)为lgif模型的分割结果；(e)为glgdf模型的分割结果；(f)为本发明所提方法的分割结果。

图5为各算法对医学图像的分割结果，其中，(a)为原始图像；(b)为lbf模型分割结果；(c)为lgdf模型分割结果；(d)为lrs模型分割结果；(e)为lgif模型分割结果；(f)为glgdf模型分割结果；(g)为本发明所提方法的分割结果。

图6为各算法对添加灰度不均匀合成图像的分割结果，其中，(a)为原始星形图像；(b)为在图像(a)中加入不均匀的灰度所产生的图像；(c)为lbf模型的分割结果；(d)为lgdf模型的分割结果；(e)为lrs模型的分割结果；(f)为lgif模型的分割结果；(g)为glgdf模型的分割结果；(h)为本发明所提方法的分割结果。

图7为各算法对灰度不均匀图像分割结果的js值。

图8为各算法在不同高斯噪声下的分割结果，其中，(a)为原始图像，真实的边界是已知的；(b)为带有初始轮廓的高斯噪声图像，其噪声水平分别为5％、10％、15％、20％、25％、30％(从上至下)；(c)为lbf模型的分割结果；(d)为lgdf模型的分割结果；(e)为lrs模型的分割结果；(f)为lgif模型的分割结果；(g)为glgdf模型的分割结果；(h)为本发明所提方法的分割结果。

图9为各算法在不同散斑噪声下的分割结果，其中，(a)为原始图像，真实的边界是已知的；(b)为带有初始轮廓的散斑噪声图像，其噪声水平分别为1％、2％、3％、4％、5％(从上至下)；(c)为lbf模型的分割结果；(d)为lgdf模型的分割结果；(e)为lrs模型的分割结果；(f)为lgif模型的分割结果；(g)为glgdf模型的分割结果；(h)为本发明所提方法的分割结果。

具体实施方式

以下是本发明的具体实施例并结合附图，对本发明的技术方案作进一步的描述，但本发明并不限于这些实施例。

如图1所示，一种基于局部高斯分布拟合与局部符号差能量驱动的活动轮廓模型图像分割方法，其特征在于，该方法包括如下步骤：

s1：输入原始图像i(x)；

s2：计算图像的局部熵，进而得到图像的局部符号差能量项，具体如下：

图像局部熵的表达式为：

公式中，ωx是以x为中心的邻域，y是邻域中的像素，p(y,ωx)是邻域像素灰度级的分布函数，可以表示为：

图像的局部符号差能量项的表达式为：

公式中，er(x)＝e(x,b(x,r))是以x为中心的邻域像素点的局部熵，b(x,r)＝{y:|x-y|≤r,r＞0}是窗口函数，

w(x)是权重函数，定义如下：

w(x)＝∫inside(c)kσ(x-y)dy∫outside(c)kσ(x-y)dy

前景聚类f1和背景聚类f2的符号差能量e^lsd(x)定义如下：

e^lsd(x)＝f1(x)-f2(x)，

s3：初始化水平集函数φ＝φ⁰(x)，它的符号距离函数定义如下：

s4：初始化系数α、β、λ1、λ2、μ、ν、ε、σ、δt；

s5：计算局部拟合能量项e1、e2，

在步骤s5中，包括如下子步骤：

s5.1：在局部高斯分布拟合能量的基础上引入局部符号差能量项

公式中，e^lgdf、e^l分别为局部高斯分布拟合能量项和局部符号差能量项，α、β分别为lgdf项和lsd项的权重系数，其中，lgdf模型的能量泛函如下所示：

s5.2：为了保持演化曲线本身的光滑度和规则性，并且尽可能减少在分割结果中出现孤立和较小的区域，需要在目标函数中引入长度项和惩罚项，则模型的能量泛函可以表示为：

公式中，l(φ)和p(φ)分别为长度项和惩罚项，ν和μ分别是它们的权重系数；

s5.3：引入heaviside函数h(z)和dirac函数δ(z)，则能量泛函可以表示为如下的水平集形式：

公式中，m1,ε(φ(y))＝hε(φ(y))；m2,ε(φ(y))＝1-hε(φ(y)),在实际过程中，heaviside函数近似为一个光滑函数hε(z)：

dirac函数δ(z)相应的正则化形式δε(z)定义如下：

s5.4：采用标准的梯度下降流法来极小化能量泛函,固定水平集函数φ，对s5.3中的水平集形式关于函数u1、u2、σ1、σ2极小化泛函f(φ)，通过变分法可得：

s5.5：固定u1、u2、σ1和σ2来最小化s5.3中的水平集形式所描述的能量泛函f(φ)，同时引入时间变量t，可得到如下的水平集演化方程：

公式中，

s6：更新水平集函数φ；

s7：判断水平集演化曲线是否满足收敛准则，若没有，转到步骤s5继续计算，直到满足终止条件。

图2为图像的局部熵显示图。其中，第一列是一幅合成噪声图像，它是在二值图像中添加了不匀均的灰度与标准差为4.0的高斯噪声所产生的；第二列是一幅真实的t型图像，由于光照产生的不均匀，导致了背景区域的亮度远大于目标区域的亮度，且图像中存在着明显的灰度不均匀现象；最后两列是血管图像，图中某些血管的边界非常模糊。从图中可以看出，在局部熵空间下，图像具有明显的背景和前景。

图3为各算法对合成噪声图像的分割结果。从实验结果可以看出，由于受初始轮廓曲线的影响，lbf、lgdf、lrs、lgif和glgdf模型只能在特定情况下才能获得准确的分割效果。相比之下，本发明所提方法的分割结果受初始轮廓曲线大小、位置、形状的影响比较小，具有更好的鲁棒性。

图4为各算法对t型图像的分割结果。通过实验分析发现，lbf和lrs模型在这五个位置都不能正确地提取出目标的边缘。lgif模型在第三个位置时得到了准确的分割结果，而其它几个初始条件下却无法获取完整的t型轮廓。lgdf和glgdf模型能够取得不错的分割效果，但在第四个位置时却出现了一定的误分割现象。然而本发明所提模型在五个不同的轮廓曲线下都能正确地提取出目标的边界，对初始轮廓曲线的依赖性更小。

图5为各算法对医学图像的分割结果。由于这些图像中含有大量的噪声，lbf和lrs模型仅仅考虑了图像的局部灰度特性，能够实现灰度不均匀目标的提取，当图像中存在局部均值变化很小的情况时也会失效。lgif模型融合了局部与全局的灰度信息，在目标边缘很弱的情况下，无法达到分割的精度要求。lgdf和glgdf模型虽然同时考虑了图像的局部均值信息和局部方差信息，能够正确地提取含有噪声和信噪比较低的图像，但也会出现分割失败的情况。然而，尽管图像中含有大量的噪声和弱边缘，本发明所提出的模型对于八幅医学图像都能准确地提取出目标的边界，这是因为该算法在考虑局部均值信息和局部方差信息的同时还引入了局部熵的概念，使得图像中背景和前景之间的对比度更加明显。表1显示了上述六种算法在进行图像分割时所需要的迭代次数和迭代时间。从表中可以看出，本发明所提出的模型具有较快的分割速度，这是因为局部熵加权的lsd能量项与水平集函数φ无关，在演化过程中仅需要计算一次，从而大大缩短了算法的运行时间。lgif模型的计算速度也很快，但处理效果明显不如本发明所提出的方法。

表1图5中各模型的分割时间和迭代次数

图6为各算法对添加灰度不均匀合成图像的分割结果。从视觉角度来看，lgdf模型、lrs模型、lgif模型和glgdf模型在某些位置会出现一定的误分割现象，而lbf模型和本发明所提出的模型都能够较好地提取出目标的边界。

图7为各算法对灰度不均匀图像分割结果的js值。为了定性地评价各算法的性能，采用js相似性系数(jaccardsimilarity)来衡量每个方法的分割精度。假定s1表示各模型分割所获得的区域，s2为给定图像的真实边界，那么js度量可以被定义为：

公式中，js的取值范围是0～1，js的值越接近1，表示图像分割的精度就越高。图7中提供了各模型对灰度不均匀图像处理结果的量化评估。由于在模型中引入了局部熵的概念，图像中背景区域和前景区域之间的对比度非常明显，使得本发明所提出的模型在抑制灰度不均匀现象时鲁棒性更强。通过定量比较可以发现，在上述的这些图像中，本发明所提出的模型所获得的js值都是最高的，说明该模型对灰度不均匀图像具有更好的分割效果。

图8为各算法在不同高斯噪声下的分割结果。为了定量地比较各模型的分割精度，采用均方根误差(rmse)来衡量分割结果与真实值之间的偏差。rmse准则定义如下：

其中，(xk,yk)(k＝0,...,n-1)表示分割后图像轮廓上点的坐标，(k＝0,...,n-1)表示真实图像轮廓上与(xk,yk)距离最近的对应点的坐标。rmse的值越小，表示分割结果与真实结果之间的差距越小，对应模型的分割精度就越高；反之，rmse的值越大，说明分割效果就越差。以没有添加高斯噪声的图像分割结果作为基准，计算各个模型的rmse值，实验结果如表2所示。从表中可以发现，在高斯噪声水平为5％时，lgdf模型所获得的rmse值是最小的；对于其余噪声水平，本发明所提出的模型模型的rmse值是最低的，这表明该模型的分割结果与真实结果之间的相似度最高，抗噪性能最好。

表2各算法对高斯噪声图像分割结果的rmse值

图9为各算法在不同散斑噪声下的分割结果。如表3所示，在散斑噪声水平为2％时，lgdf模型的rmse值是最小的；对于其余四种噪声水平，本发明所提出模型所获得的rmse值是最低的，该模型在分割精度方面要优于其它五种方法。

表3各算法对散斑噪声图像分割结果的rmse值

本文中所描述的具体实施例仅仅是对本发明精神作举例说明。本发明所属技术领域的技术人员可以对所描述的具体实施例做各种各样的修改或补充或采用类似的方式替代，但并不会偏离本发明的精神或者超越所附权利要求书所定义的范围。本文并不排除使用其它术语的可能性。使用这些术语仅仅是为了更方便地描述和解释本发明的本质；把它们解释成任何一种附加的限制都是与本发明精神相违背的。