一种基于Benbow－Bridgwater模型的三点法表征挤出压力的方法与流程

本发明涉及一种挤出压力的表征方法，具体是一种基于benbow-bridgwater模型的挤出压力的表征方法，属于材料挤出技术领域。

背景技术：

材料挤出技术在许多领域有非常重要的应用，如增材制造(3d打印)领域，2012年1月，美国材料与试验协会f42增材制造委员会对增材制造技术进行了标准化，材料挤出是7种主要的增材制造技术之一，具有非常广泛的应用前景和重要的应用价值。挤出压力表征是材料挤出技术能否成功实现的最为关键的因素之一，1993年，johnbenbow和johnbridgwater建立了糊剂材料流动和挤出的模型，称之为benbow-bridgwater模型，该模型成为研究糊剂材料流动和挤出特征的经典模型之一，国内外许多研究人员在此模型基础上开展了广泛而深入的研究，例如：2002年，英国剑桥大学的peterjamesmartin将benbow-bridgwater模型作为工具之一，研究了径向筛机糊剂流动的力学性能；2017年，英国南安普顿大学的mohammadvaezi基于benbow-bridgwater模型，开展了低温挤出3d打印组织工程支架的研究。尽管如此，如何表征挤出压力一直是材料挤出成败的关键技术之一。传统的挤出压力表征方法认为挤出压力与喷嘴的长径比(l/d)成线性关系，因此采用单点插入法估算当l/d＝0时的挤出压力p0值。但在糊剂材料实际挤出过程中，即使在稳定状态下，由于糊剂材料中夹带的空气气泡、团聚等原因导致糊剂材料的局部不均匀使得挤出压力产生波动，因此，用单点插入法表征挤出压力的方法造成挤出压力预测值与实测值之间产生了比较大的误差，这对材料挤出系统及工艺参数优化是非常不利的，影响挤出精度，严重时将会导致挤出过程失败。

技术实现要素：

为解决上述问题，本发明的目的是提供一种基于benbow-bridgwater模型的三点法表征挤出压力的方法，以提高挤出压力表征精度，有利于挤出系统及工艺参数的优化。

为了达到上述目的，本发明采用的技术方案是：一种基于benbow-bridgwater模型的三点法表征挤出压力的方法，所述的benbow-bridgwater模型的挤出压力公式为其中，p表示挤出压力值，d0表示盛装糊剂材料的桶的直径，l和d表示喷嘴(或毛细管)的长度和直径，f(v)表示糊剂材料在挤出压力作用下从盛装桶流向毛细管这段过程中与糊剂的挤出速度(v)相关的函数，g(v)表示糊剂在挤出压力作用下在毛细管中流动并从喷嘴口挤出的这段过程中与糊剂的挤出速度(v)相关的函数，其特征在于，它是按下列步骤进行：

(1)三点试验获取挤出压力值pi

s1：分别用三种不同长径比(l/d)的喷嘴以同样的挤出速度(v)进行挤出试验，获取在稳定状态下的挤出压力值pi(i＝1，2，3)；

(2)计算当喷嘴长径比等于零时的平均挤出压力p0

s2：建立平面xoy坐标系，其中，x坐标轴表示喷嘴的长径比(l/d)，y坐标轴表示挤出压力p，挤出压力值pi在平面xoy坐标系中按照x坐标轴的大小顺序排列，分别表示为p1(x1，y1)，p2(x2，y2)，p3(x3，y3)；连接p2、p1点并延长p2p1与y坐标轴相交，得到交点p012(0，y012)，连接p3、p1点并延长p3p1与y坐标轴相交，得到交点p013(0，y013)，连接p3、p2点并延长p3p2与y坐标轴相交，得到交点p023(0，y023)，根据几何学原理，可以得到以下公式：

公式(1)经过数学变换后，得到公式(2)：

同理可以得到以下公式：

s3：于是，可以得到当喷嘴长径比等于零时的平均挤出压力p0为：

(3)获取三点法表征挤出压力的分析模型

s4：将公式(5)带入到benbow-bridgwater模型中，得到在一定的挤出速度(v)下的平均f(v)值，如公式(6)所示：

s5：将三种不同长径比(l/d)试验得到的pi值带入到benbow-bridgwater模型中，得到gi(v)值，如公式(7)所示：

s6：平均三次gi(v)值，得到在一定的挤出速度(v)下的平均g(v)值，如公式(8)所示：

s7：以至少三种不同的挤出速度重复所述的s1-s6步骤，得到不同挤出速度下的离散数据集f(v)和g(v)；

s8：基于最小二乘法理论，获得s7步骤所述的离散数据集f(v)和g(v)在任意挤出速度(v)时的逼近函数fh(v)和gh(v)，带入到benbow-bridgwater模型中，如公式(9)所示：

从而得到挤出压力与挤出速度以及挤出器结构之间的函数关系，获得三点法表征挤出压力的分析模型，用于挤出压力的表征以优化挤出系统及工艺参数。

本发明的有益效果是：本发明的一种基于benbow-bridgwater模型的三点法表征挤出压力的方法，改变了传统的单点法估算挤出压力的表征方法，提高了挤出压力表征精度，有利于材料挤出系统及工艺参数的优化。

附图说明

图1是糊剂材料挤出benbow-bridgwater模型示意图；

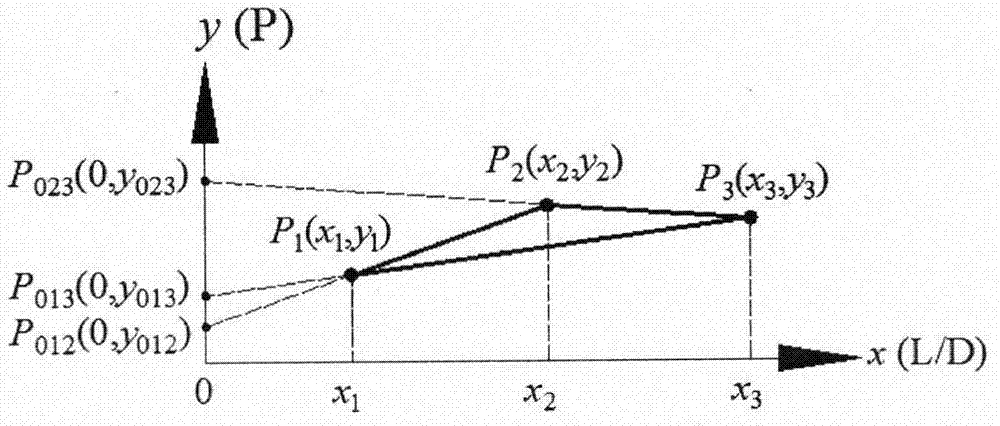
图2是本发明三点法表征挤出压力的示意图。

附图中的序号表示如下：1、盛装糊剂材料的桶；2、压头；3、挤出压力；4、糊剂材料；5、喷嘴(或毛细管)；6、挤出物；7、挤出速度(v)；8、喷嘴口。

具体实施方式

下面结合附图和实施例，对本发明作进一步地说明：

图1解释了糊剂材料在挤出压力作用下从盛装糊剂材料的桶流向毛细管并从喷嘴口挤出过程的benbow-bridgwater模型示意图，如图1所示，糊剂材料4被盛装在直径为d0的桶1中，压头2在挤出压力3的作用下将糊剂材料4压入到具有直径为d、长度为l的喷嘴(或毛细管)5中。在从桶体1进入到喷嘴5的过程中，糊剂材料4沿着流动方向延伸并且其横截面减小，并以挤出速度(v)7从喷嘴口8流出，形成挤出物6。毛细管5的重要特征是直径d非常小，糊剂材料在毛细管中的流动只有层流式而没有湍流式，因此，基于此，我们可以从糊剂流动的试验测量中找出糊剂材料的流变性质。

johnbenbow和johnbridgwater认为，糊剂材料在挤出过程中，其挤出压力与糊剂材料的流变性质以及挤出器的结构相关，benbow-bridgwater模型的挤出压力公式之一为其中，p表示挤出压力值，d0表示盛装糊剂材料的桶的直径，l和d表示喷嘴(或毛细管)的长度和直径，f(v)表示糊剂材料在挤出压力作用下从盛装桶流向毛细管这段过程中与糊剂的挤出速度(v)相关的函数，g(v)表示糊剂在挤出压力作用下在毛细管中流动并从喷嘴口挤出的这段过程中与糊剂的挤出速度(v)相关的函数。传统的挤出压力表征方法认为挤出压力与喷嘴的长径比(l/d)成线性关系，因此采用单点插入法估算当l/d＝0时的挤出压力p0值，但存在挤出压力预测值与实测值之间误差较大的问题，不利于材料挤出系统及工艺参数优化。为此，本发明提供一种基于benbow-bridgwater模型的三点法表征挤出压力的方法，以提高表征精度，有利于材料挤出系统及工艺参数的优化。

为了达到上述目的，本发明采用的技术方案如图2所示，其特征在于，它是按下列步骤进行：

(1)三点试验获取挤出压力值pi

s1：分别用三种不同长径比(l/d)的喷嘴以同样的挤出速度(v)进行挤出试验，获取在稳定状态下的挤出压力值pi(i＝1，2，3)；

(2)计算当喷嘴长径比等于零时的平均挤出压力p0

s2：建立平面xoy坐标系，其中，x坐标轴表示喷嘴的长径比(l/d)，y坐标轴表示挤出压力p，挤出压力值pi在平面xoy坐标系中按照x坐标轴的大小顺序排列，分别表示为p1(x1，y1)，p2(x2，y2)，p3(x3，y3)；连接p2、p1点并延长p2p1与y坐标轴相交，得到交点p012(0，y012)，连接p3、p1点并延长p3p1与y坐标轴相交，得到交点p013(0，y013)，连接p3、p2点并延长p3p2与y坐标轴相交，得到交点p023(0，y023)，根据几何学原理，可以得到以下公式：

公式(1)经过数学变换后，得到公式(2)：

同理可以得到以下公式：

s3：于是，可以得到当喷嘴长径比等于零时的平均挤出压力p0为：

(3)获取三点法表征挤出压力的分析模型

s4：将公式(5)带入到benbow-bridgwater模型中，得到在一定的挤出速度(v)下的平均f(v)值，如公式(6)所示：

s5：将三种不同长径比(l/d)试验得到的pi值带入到benbow-bridgwater模型中，得到gi(v)值，如公式(7)所示：

s6：平均三次gi(v)值，得到在一定的挤出速度(v)下的平均g(v)值，如公式(8)所示：

s7：以至少三种不同的挤出速度重复所述的s1-s6步骤，得到不同挤出速度下的离散数据集f(v)和g(v)；

s8：基于最小二乘法理论，获得s7步骤所述的离散数据集f(v)和g(v)在任意挤出速度(v)时的逼近函数fh(v)和gh(v)，带入到benbow-bridgwater模型中，如公式(9)所示：

从而得到挤出压力与挤出速度以及挤出器结构之间的函数关系，获得三点法表征挤出压力的分析模型，用于挤出压力的表征以优化挤出系统及工艺参数。

具体实施例以2017年英国南安普顿大学的mohammadvaezi的博士论文“3dprintingofbonetissueengineeringscaffoldsandproductionofpeek-basedbiocomposites”中的l27(3¹³)正交试验数据为依据，进行传统单点法和本发明提出的三点法进行对比，分析两种方法对挤出压力的表征精度，试验因素和水平如表1所示

表1试验因素和水平

考虑到有三个控制因素，每个因素有三个水平，以及三个交互作用，共18个自由度，故该试验采用l27(3¹³)正交表进行正交试验，l27(3¹³)正交表有13列用于放置控制因素，有27行用于开展试验，为了避免人为因素导致的系统误差，控制因素a、b、c被随机放置在第1、2、6列，为减少误差，每次试验进行3次，所有的挤出压力测定值是在稳定阶段3次试验读数的平均值。

mohammadvaezi采用单点法进行了挤出压力的表征，用单点法并基于最小二乘法理论获得的fh(v)和gh(v)函数为

作为对比，本发明采用三点法进行挤出压力的表征，用三点法并基于最小二乘法理论获得的fh(v)和gh(v)函数为

将公式(10)和(11)分别带入到公式(9)中，并将正交试验的27个试验条件插入到单点法和三点法中，得到单点法与三点法两种方法的挤出压力表征结果，如表2所示

表2l27(3¹³)正交试验结果及单点法、三点法表征结果

由表2可知，三点法的表征精度明显高于单点法的表征精度，表明本发明提出的三点法表征挤出压力的方法，改变了传统的单点法估算挤出压力的表征方法，提高了挤出压力表征精度，有利于材料挤出系统及工艺参数的优化，可以作为挤出压力表征的一般方法。

本发明涉及的其他未说明部分与现有技术相同。

上述具体实施例用来解释说明本发明，而不是对本发明进行限制，在本发明的精神和权利要求的保护范围内，凡对本发明采取等同替换或等效变换所获得的技术方案，都落入本发明的保护范围。