一种基于断点模型的数控磨床液压系统故障树分析方法与流程

本发明属于数控磨床可靠性分析领域，更具体地，涉及一种基于断点模型的数控磨床液压系统故障树分析方法。

背景技术：

传统的故障树分析方法以布尔代数和概率论为基础，故障树由事件和门组成，事件的发生由故障概念来描述，事件的联系用门来描述。这种分析方法在液压系统的可靠性分析中得以广泛研究和应用。

目前故障树分析技术存在的问题主要有三点：1、机械零件的故障数据无法比较精确得到，导致以重要度为计算方法的理论失效；2、机械产品故障的连锁比较长，必然导致可能性越来越分散，即出现小概率的断点(高等数学中的断点的延伸)；3、故障树分析的本质原因难以确定，即难于找出所有可能的原因。其次，在对磨床液压系统进行故障树分析时，会遇到两种比较特殊的情况。一种是中间事件本身发生的概率很小，且中间事件和顶事件的关联程度较小，那么对该事件下联的底事件进行改进所得到的经济效益就会相对较低。另一种是中间事件发生的概率较小，在现有条件下对该事件下联的底事件进行控制的成本(设计、改进、装配等方面的改进)很高，那么对该事件进行控制就会耗费大量的成本，且其对顶事件的影响也不大，对其进行控制后所得的经济效益仍然较低。

因此，怎样提供一种能够缩短改进过程、降低改进成本以及提高产品经济效益的基于断点模型的数控磨床液压系统故障树分析方法，成为有待本领域人员考虑解决的问题。

技术实现要素：

针对现有技术存在的上述不足，本发明所要解决的技术问题是：怎样提供一种能够缩短改进过程、降低改进成本以及提高产品经济效益的基于断点模型的数控磨床液压系统故障树分析方法。

为了解决上述技术问题，本发明采用了如下的技术方案：

一种基于断点模型的数控磨床液压系统故障树分析方法，其特点在于，基于故障树分析方法，通过综合考虑事件本身发生的概率大小，事件与上层事件的关联程度以及事件的改进成本三因素来剃除故障树中发生概率小于预设值、事件与上层事件的关联程度小于预设值以及事件的改进成本大于预设值的中间事件下属的子故障树，再进行故障树分析。

本技术方案中，在对故障进行分析时，综合考虑事件本身的概率大小，事件与上层事件的关联程度以及事件的改进成本，综合以上三个因素来确定事件进行改进的必要性。剃除故障树中发生概率小于预设值、事件与上层事件的关联程度小于预设值以及事件的改进成本大于预设值的中间事件下属的子故障树，在新的故障树中确定优先改进和控制的中间事件，更加符合工程实际的需要。使得在进行故障分析时更加的全面和高效，同时将改进成本结合到故障树分析中，充分考虑到工程实际情况，使得最终分析结果具有更高的可操作性，能够降低改进成本，能够缩短改进过程，提高产品经济效益。

作为优化，其中通过综合考虑事件本身发生的概率大小，事件与上层事件的关联程度以及事件的改进成本三因素来剃除故障树中发生概率小于预设值、事件与上层事件的关联程度小于预设值以及事件的改进成本大于预设值的中间事件下属的子故障树包括以下步骤，1引入中间事件断点值bp，建立断点模型bp＝f(x,y)，其中bp称为断点值，bp是一个关于变量x和y的二元函数，其中x代表事件的概率与关联程度等级，y代表控制事件发生所要付出的成本等级；2建立机电产品的概率与关联程度等级以及建立机电产品的成本等级；3定义概率断点和成本断点，事件的bp＝1，称该事件为故障树的断点，此时剃除该事件下联的子故障树，得到新的故障树。

这样，通过引入中间事件断点值bp，建立断点模型bp＝f(x,y)其中bp称为断点值，再通过建立机电产品的概率与关联程度等级以及建立机电产品的成本等级，得到断点模型中x和y的值，通过断点模型分析得到断点，这样能够使得整个分析方法得出的结论更加的稳定，更加可靠。

作为优化，所述步骤2具体操作为，

一、建立机电产品的概率与关联程度等级，

由于机电产品缺乏电子产品的元器件可靠性数据，因此对底事件概率需要通过等级来描述，判断一个事件的概率与关联程度等级，主要考虑两方面因素，第一，事件本身的概率大小；第二，事件与上层事件的关联程度；根据经验与售后维修记录对事件的发生概率进行评价，将其分为四个等级，即经常发生，有时发生、偶然发生与很少发生；

概率大小与评分对应关系见表1，

将事件与上层事件的关联程度进行评价，同样分为四个等级，即高度相关，中度相关、一般相关与较小相关；

关联程度与评分对应关系见表2

表2，关联程度与评分对应关系

综合事件本身的概率大小以及事件与上层事件关联程度两方面因素，确定x的定义域；

见表3可得x的定义域为{x|x＝0,1,2,3,4,5,6}；

表3，x的取值范围

二、建立机电产品的成本等级，

判断事件的改进成本则需要从多个方面进行考虑，对某项缺陷进行改进会引起其他改动，因此从设计改动量、加工改动量、装配改动量、硬件成本、时间成本等进行评价，采用专家评分法，

专家评分原则如下：

1)设计改动量，是根据事件所造成的设计改动量的多少来评定的，设计改动量最多的评10分，没有改动则评0分，设计改动量处于改动量最多和没有改动之间的部分均匀的分为9个等级并依次给定分数为9、8、7、6、5、4、3、2、1；

2)加工改动量，根据事件所造成的加工改动量的多少来评定的，加工改动量最多的评10分，没有改动则评0分，加工改动量处于改动量最多和没有改动之间的部分均匀的分为9个等级并依次给定分数为9、8、7、6、5、4、3、2、1；

3)装配改动量，根据事件所造成的装配改动量来评定，装配改动量最多的评10分，没有改动则评0分，装配改动量处于改动量最多和没有改动之间的部分均匀的分为9个等级并依次给定分数为9、8、7、6、5、4、3、2、1；

4)硬件成本，根据事件消耗的硬件成本大小来评定，消耗硬件成本最多的评10分，最少的评0分，消耗硬件成本处于消耗最多和消耗最少之间的部分均匀的分为9个等级并依次给定分数为9、8、7、6、5、4、3、2、1；

5)时间成本，根据改进设计所消耗的时间成本大小来评定，消耗时间成本最多的评10分，最少的0分，消耗的时间成本处于消耗时间最多和消耗时间最少之间的部分均匀的分为9个等级并依次给定分数为9、8、7、6、5、4、3、2、1；

每一事件的总评分为设计改动量、加工改动量、装配改动量、硬件成本和时间成本五个因素求和，总的评分取值范围为0-50，将其均匀分为5个评分等级，每一评分等级与y值一一对应，见表4，

表4事件成本分数范围与y取值对应关系

选取生产专家和管理专家，对生产过程中的改进成本打分，并对评价进行等级划分，本专利根据实际情况将其划分为五个等级，每个等级对应相应的分数段，将控制事件所要付出的成本定为y，则y{y|y＝0,1,2,3,4}；

改进成本评价见表5，

其中，c1表示表示设计改动量、c2表示加工改动量、c3表示装配改动量、c4表示硬件成本、c5表示时间成本，g1表示事件的总评分，i表示事件e1的取值范围，

所述步骤3具体操作为，

一、定义概率断点和成本断点，

事件本身发生的概率很小，而且其与顶事件的关联程度较低，即x取值为0或1时，bp为1，这类断点称为概率断点；事件本身发生的概率较小，而且在现有条件下对事件改进的成本很高，即x＝2且y＝3或4时，bp为1，这类断点定义为成本断点；

故断点函数模型如下：

a＝{(x,y)|x＝0,1,2,3,4,5,6,y＝0,1,2,3,4}(3)

b＝{(x,y)|x＝0,1,y＝0,1,2,3,4}或{(x,y)|x＝2,y＝3,4}(4)

二、剃除断点下联子故障树，得到新的故障树，

结合专家评分法对顶事件下的第一层中间事件进行评价，若在第一层中间事件中没有找到断点，则继续对第二层中间事件进行判断；剃除相应断点下联的子故障树，继续对下一层中间事件进行判断，找出断点，并继续剃除断点下联的子故障树，继续寻找断点直至底事件的上一层事件为止，最终得到一个简化的故障树，该故障树中的底事件是需要重点改进的对象。

作为优化，对简化的故障树的第三层中间事件改进顺序排序，在各事件中，针对专家评分结果得到第三层中间事件对应的(x，y)，对中间事件的改进顺序进行排序，概率与关联程度等级较高、成本等级较低的底事件，作为排查故障时优先考虑的底事件；

由如下步骤确定第三层中间事件的改进顺序：

1)首先计算所有中间事件的p值，其中p＝x-y，p表示事件的优先改进值；

2)比较各中间事件p的大小，优先改进p值最大的中间事件；

3)当p值相同时，优先改进x值较大的中间事件；

4)当p值相同时，若此时存在y≥3的中间事件，则优先改进y值较小的中间事件。

相比现有技术，本发明具有如下优点：

1、综合考虑事件本身的概率大小，事件与上层事件的关联程度以及事件的改进成本来确定事件进行改进的必要性。找出故障树中的断点，剃除断点下联的子故障树，同时确定优先改进和控制的中间事件，以此简化故障树，更加符合工程实际的需要。

2、利用专家评分法描述了事件发生的概率大小等级、中间事件与顶事件的关联程度，可以允许评价过程中存在一定程度的偏差。同时将事件的改进成本也结合到故障树分析中，充分考虑到工程实际情况。利用专家评分法还能有效规避机械零部件失效率的历史数据和资料的缺乏、系统环境的变化以及新部件的使用，故障概率获取非常困难，具有不确定性等难操作的因素。

3、传统的故障树分析方法是找出导致顶事件的所有底事件，如果对所有的底事件进行改进，改进过程中耗费时间过长，成本过高。利用断点模型找出故障树中的断点并剃除断点下联的子故障树，有效缓解了工程实际中故障改进时改进过程过长、改进成本过高的问题，有效提高了产品的经济效益。

附图说明

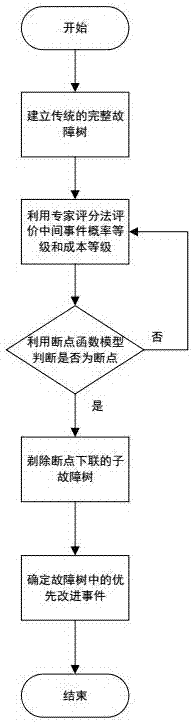
图1为本发明的分析流程图。

图2为数控磨床液压系统功能结构层次对应图。

图3为液压系统的完整故障树。

图4为基于断点模型的改进后的故障树。

具体实施方式

下面结合附图对本发明作进一步的详细说明。

具体实施时：一种基于断点模型的数控磨床液压系统故障树分析方法，基于故障树分析方法，通过综合考虑事件本身发生的概率大小，事件与上层事件的关联程度以及事件的改进成本三因素来剃除故障树中发生概率小于预设值、事件与上层事件的关联程度小于预设值以及事件的改进成本大于预设值的中间事件下属的子故障树，再进行故障树分析。

本技术方案中，在对故障进行分析时，综合考虑事件本身的概率大小，事件与上层事件的关联程度以及事件的改进成本，综合以上三个因素来确定事件进行改进的必要性。剃除故障树中发生概率小于预设值、事件与上层事件的关联程度小于预设值以及事件的改进成本大于预设值的中间事件下属的子故障树，在新的故障树中确定优先改进和控制的中间事件，更加符合工程实际的需要。使得在进行故障分析时更加的全面和高效，同时将改进成本结合到故障树分析中，充分考虑到工程实际情况，使得最终分析结果具有更高的可操作性，够降低改进成本，能够缩短改进过程，提高产品经济效益。

本具体实施方案中，其中通过综合考虑事件本身发生的概率大小，事件与上层事件的关联程度以及事件的改进成本三因素来剃除故障树中发生概率小于预设值、事件与上层事件的关联程度小于预设值以及事件的改进成本大于预设值的中间事件下属的子故障树包括以下步骤，1引入中间事件断点值bp，建立断点模型bp＝f(x,y)，其中bp称为断点值，bp是一个关于变量x和y的二元函数，其中x代表事件的概率与关联程度等级，y代表控制事件发生所要付出的成本等级；2建立机电产品的概率与关联程度等级以及建立机电产品的成本等级；3定义概率断点和成本断点，事件的bp＝1，称该事件为故障树的断点，此时剃除该事件下联的子故障树，得到新的故障树。

这样，通过引入中间事件断点值bp，建立断点模型bp＝f(x,y)其中bp称为断点值，再通过建立机电产品的概率与关联程度等级以及建立机电产品的成本等级，得到断点模型中x和y的值，通过断点模型分析得到断点，这样能够使得整个分析方法得出的结论更加的稳定，更加可靠。

本具体实施方案中，所述步骤2具体操作为，

一、建立机电产品的概率与关联程度等级，

由于机电产品缺乏电子产品的元器件可靠性数据，因此对底事件概率需要通过等级来描述，判断一个事件的概率与关联程度等级，主要考虑两方面因素，第一，事件本身的概率大小；第二，事件与上层事件的关联程度；根据经验与售后维修记录对事件的发生概率进行评价，将其分为四个等级，即经常发生，有时发生、偶然发生与很少发生；

概率大小与评分对应关系见表1，

将事件与上层事件的关联程度进行评价，同样分为四个等级，即高度相关，中度相关、一般相关与较小相关；

关联程度与评分对应关系见表2

表2，关联程度与评分对应关系

综合事件本身的概率大小以及事件与上层事件关联程度两方面因素，确定x的定义域；

见表3可得x的定义域为{xx＝0,1,2,3,4,5,6}；

表3，x的取值范围

二、建立机电产品的成本等级，

判断事件的改进成本则需要从多个方面进行考虑，对某项缺陷进行改进会引起其他改动，因此从设计改动量、加工改动量、装配改动量、硬件成本、时间成本等进行评价，采用专家评分法，

专家评分原则如下：

1)设计改动量，是根据事件所造成的设计改动量的多少来评定的，设计改动量最多的评10分，没有改动则评0分，设计改动量处于改动量最多和没有改动之间的部分均匀的分为9个等级并依次给定分数为9、8、7、6、5、4、3、2、1；

2)加工改动量，根据事件所造成的加工改动量的多少来评定的，加工改动量最多的评10分，没有改动则评0分，加工改动量处于改动量最多和没有改动之间的部分均匀的分为9个等级并依次给定分数为9、8、7、6、5、4、3、2、1；

3)装配改动量，根据事件所造成的装配改动量来评定，装配改动量最多的评10分，没有改动则评0分，装配改动量处于改动量最多和没有改动之间的部分均匀的分为9个等级并依次给定分数为9、8、7、6、5、4、3、2、1；

4)硬件成本，根据事件消耗的硬件成本大小来评定，消耗硬件成本最多的评10分，最少的评0分，消耗硬件成本处于消耗最多和消耗最少之间的部分均匀的分为9个等级并依次给定分数为9、8、7、6、5、4、3、2、1；

5)时间成本，根据改进设计所消耗的时间成本大小来评定，消耗时间成本最多的评10分，最少的0分，消耗的时间成本处于消耗时间最多和消耗时间最少之间的部分均匀的分为9个等级并依次给定分数为9、8、7、6、5、4、3、2、1；

每一事件的总评分为设计改动量、加工改动量、装配改动量、硬件成本和时间成本五个因素求和，总的评分取值范围为0-50，将其均匀分为5个评分等级，每一评分等级与y值一一对应，见表4，

表4事件成本分数范围与y取值对应关系

选取生产专家和管理专家，对生产过程中的改进成本打分，并对评价进行等级划分，本专利根据实际情况将其划分为五个等级，每个等级对应相应的分数段，将控制事件所要付出的成本定为y，则y{y|y＝0,1,2,3,4}；

改进成本评价见表5，

表5改进成本评价

其中，c1表示表示设计改动量、c2表示加工改动量、c3表示装配改动量、c4表示硬件成本、c5表示时间成本，g1表示事件的总评分，i表示事件e1的取值范围，

所述步骤3具体操作为，

一、定义概率断点和成本断点，

事件本身发生的概率很小，而且其与顶事件的关联程度较低，即x取值为0或1时，bp为1，这类断点称为概率断点；事件本身发生的概率较小，而且在现有条件下对事件改进的成本很高，即x＝2且y＝3或4时，bp为1，这类断点定义为成本断点；

故断点函数模型如下：

a＝{(x,y)|x＝0,1,2,3,4,5,6,y＝0,1,2,3,4}(3)

b＝{(x,y)|x＝0,1,y＝0,1,2,3,4}或{(x,y)|x＝2,y＝3,4}(4)

二、剃除断点下联子故障树，得到新的故障树，

结合专家评分法对顶事件下的第一层中间事件进行评价，若在第一层中间事件中没有找到断点，则继续对第二层中间事件进行判断；剃除相应断点下联的子故障树，继续对下一层中间事件进行判断，找出断点，并继续剃除断点下联的子故障树，继续寻找断点直至底事件的上一层事件为止，最终得到一个简化的故障树，该故障树中的底事件是需要重点改进的对象。

本具体实施方案中，对简化的故障树的第三层中间事件改进顺序排序，在各事件中，针对专家评分结果得到第三层中间事件对应的(x，y)，对中间事件的改进顺序进行排序，概率与关联程度等级较高、成本等级较低的底事件，作为排查故障时优先考虑的底事件；

由如下步骤确定第三层中间事件的改进顺序：

1)首先计算所有中间事件的p值，其中p＝x-y，p表示事件的优先改进值；

2)比较各中间事件p的大小，优先改进p值最大的中间事件；

3)当p值相同时，优先改进x值较大的中间事件；

4)当p值相同时，若此时存在y≥3的中间事件，则优先改进y值较小的中间事件。

具体实施实例，

基于断点模型的数控磨床液压系统故障树分析方法，其分析流程如图1所示，包括建立传统的完整的故障树，利用专家评分法评价中间事件概率与关联程度等级和成本等级，利用断点模型判断是否为断点，剃除断点下联的子故障树，对故障树的底事件改进顺序进行排序。

如图2所示，数控磨床液压系统由油源组件、动力组件、控制组件和执行组件组成。液压系统作为数控磨床重要组成部分，其功能为为工作台提供动力，为润滑系统提供润滑油,实现工作台移动与润滑工作台。

本具体实施实例中的基于断点模型的数控磨床液压系统故障树分析方法按照以下步骤实施：

步骤1：采用传统的故障树分析方法建立完整的故障树。

以液压系统油压不足作为顶事件，驱动机械功率过小，液压系统漏油，液压泵故障作为第二层事件，通过逻辑门层层相连，建立液压系统油压不足的静态故障树，如附图3所示。对各中间事件和底事件进行编码，如表6所示。

表6事件编号及描述

步骤2：利用断点函数模型找出静态故障树中的断点，

1、从故障树的顶部由上至下，利用专家评分法依次对中间事件评价。首先利用专家评分法对第一层中间事件e1，e2，e3概率与关联程度等级(见表7)和成本等级(见表8)进行评价。

表7第一层中间事件概率与关联程度等级评价

表8第一层中间事件改进成本评价

由断点函数模型公式2可得：

bp1＝f(x,y)＝f(5,3)＝0,bp2＝f(x,y)＝f(6,3)＝0,bp3＝f(x,y)＝f(4,4)＝0

由此可知第一层中间事件中没有断点。

2、在第一层中间事件中没有找到断点，计算第二层中间事件(e4～e10)中的断点函数值。利用专家评分法确定第二层中间事件概率和关联程度等级x(见表9)和成本等级y(见表10)。

表9第二层中间事件概率与关联程度等级评价

表10第二层中间事件改进成本评价

由断点函数模型公式2可得

bp4＝f(x,y)＝f(4,2)＝0,bp5＝f(x,y)＝f(4,3)＝0,bp6＝f(x,y)＝f(5,1)＝0

bp7＝f(x,y)＝f(6,2)＝0,bp8＝f(x,y)＝f(5,2)＝0,bp9＝f(x,y)＝f(6,2)＝0

bp10＝f(x,y)＝f(6,4)＝0

在第二层中间事件中没有断点。

3、计算第三层中间事件中的断点函数值。利用专家评分法确定第三层中间事件概率和关联程度等级x(见表11)和成本等级y(见表12)。

表11第三层中间事件概率与关联程度等级评价

表12第三层中间事件改进成本评价

由断点函数模型公式2可得：

bp11＝f(x,y)＝f(2,3)＝1,bp12＝f(x,y)＝f(1,3)＝1,bp13＝f(x,y)＝f(4,2)＝0

bp14＝f(x,y)＝f(6,1)＝0,bp15＝f(x,y)＝f(5,0)＝0,bp16＝f(x,y)＝f(4,0)＝0

bp17＝f(x,y)＝f(1,1)＝1,bp18＝f(x,y)＝f(5,2)＝0,bp19＝f(x,y)＝f(4,1)＝0

bp20＝f(x,y)＝f(2,3)＝1,bp21＝f(x,y)＝f(3,1)＝0

故e11，e20是成本类断点，e12，e17是概率类断点。剃除e11，e12，e17，e20下联的子故障树。

4、计算第四层中间事件中的断点函数值。利用专家评分法确定第四层中间事件概率和关联程度等级x(见表13)和成本等级y(见表14)。

表13第四层中间事件概率和关联程度等级

表14第四层中间事件改进成本评价

由断点函数模型公式2可得：

bp22＝f(x,y)＝f(4,1)＝0,bp23＝f(x,y)＝f(4,2)＝0,bp24＝f(x,y)＝f(4,2)＝0

bp25＝f(x,y)＝f(2,3)＝1,bp26＝f(x,y)＝f(5,1)＝0

在第四层中间事件中e25是成本类断点，没有概率类断点。剃除e25下联的子故障树。

5、计算第五层中间事件中的断点函数值。利用专家评分法确定第五层中间事件概率和关联程度等级x(见表15)和成本等级y(见表16)。

表15第五层中间事件概率和关联程度等级

表16第五层中间事件改进成本评价

由断点函数模型公式2可得：

bp27＝f(x,y)＝f(2,2)＝0

e27不是断点。至此，找出了所有的断点。其中e11，e20，e25是成本类断点，e12，e17是概念类断点。剃除断点下联的子故障树。

步骤3：剃除断点下联的故障树后，画出简化改进后的故障树，见附图4。在改进后的故障树中，比较第三层中间事件(e11～e21)的概率和关联程度等级以及成本等级，找出概率和关联程度等级高，成本等级低的中间事件，以此作为优先进行改进的评价标准之一。

根据公式p＝x-y确定第三层中间事件改进的先后顺序，各事件优先改进值p值见表17

表17各事件p值

由表7以及确定改进顺序的步骤可知，第三层中间事件改进的先后顺序为e14，e15，e16，e18，e19，e13，e21，e17，e11，e20，e12。

故在产品改进成本有限的情况下，优先改进e14，e15，e16下联的底事件。