一种涡轮叶片扇形孔气膜冷却结构气动‑热协同优化方法与流程

本发明涉及一种涡轮叶片扇形孔气膜冷却结构气动-热协同优化方法，属于强化冷却技术领域。

背景技术：

在航空燃气涡轮发动机的技术发展过程中，压气机增压比和涡轮进口燃气温度呈现不断增加的趋势。根据先进航空燃气涡轮发动机技术的未来的发展趋势，新一代发动机推重比将达到15左右，届时涡轮进口燃气温度将达到2200k-2300k。涡轮进口燃气温度的提升极大的加剧了涡轮叶片、燃烧室火焰筒以及排气喷管等热端部件的热载荷；同时，压气增压比的提高也导致用于热端部件的冷却空气品质降低。因此热端部件冷却技术是提高燃气涡轮发动机关键技术问题。

气膜冷却作为一种高效冷却方式，被广泛应用于航空发动机涡轮叶片上。其原理为从高温壁面的气膜孔向主流引入二次冷却气流，这股冷却气流在主流的压力和摩擦力作用下向下游弯曲，附着在壁面一定区域上，形成温度较低的冷气膜将壁面同高温燃气隔离，并带走部分高温燃气，从而对壁面起到良好的冷却保护作用。以最少的冷气量，在兼顾气动损失的情况下，产生最大的冷却效率一直是气膜冷却研究的重点。传统的气膜孔冷却结构优化需要依靠大量的实验和数值模拟来总结规律，不仅需要耗费大量的时间，而且成本相对较高。

技术实现要素：

发明目的：针对上述现有技术，提出一种涡轮叶片扇形孔气膜冷却结构气动-热协同优化方法，由涡轮叶片扇形孔气膜冷却结构向气膜冷却气动参数和热参数的非线性映射，具有预测精度高，效率高，以及良好的全局逼近能力。

技术方案：一种涡轮叶片扇形孔气膜冷却结构气动-热协同优化方法，包括以下步骤：

步骤1，确立气膜冷却结构的待优化设计变量以及待优化设计变量的范围；

步骤2，设计径向基神经网络代理模型的数据样本；

步骤3，对数据样本建立cfd模型，并计算目标函数值fobj,cal；

步骤4，利用训练样本和测试样本，训练和测试径向基神经网络；

步骤5，输出径向基神经网络预测目标函数值fobj,pre和测试样本目标函数值fobj.test最小误差下的扩展速度；

步骤6，利用粒子群算法耦合径向基神经网络搜索最优设计点；

步骤7，对优化设计点进行cfd评估，如果径向基神经网络预测目标函数值fobj,pre与cfd计算目标函数值fobj,cal误差大于5％，则将此优化设计点扩充为训练样本数据库，重新从步骤4开始迭代，直到径向基神经网络预测目标函数值fobj,pre与cfd计算目标函数值fobj,cal误差在预设范围内，迭代终止，得到全局最优设计点。

进一步的，步骤1中所述待优化设计变量包括如下参数：涡轮叶片扇形孔倾斜角α，扇形孔侧向扩展角β，扇形孔前向扩展角γ，其对应变化范围分别为25-55°，10-20°，3-15°。

进一步的，步骤2中所述数据样本的设计步骤包括：

步骤2.1，采用拉丁超立方设计方法，对待优化参数涡轮叶片扇形孔倾斜角α，扇形孔侧向扩展角β，扇形孔前向扩展角γ设计25组数据，作为训练样本；

步骤2.2，对待优化参数涡轮叶片扇形孔倾斜角α，扇形孔侧向扩展角β，扇形孔前向扩展角γ进行随机组合，设计8组数据，作为测试样本；

步骤2.3，对待优化参数进行归一化处理，其方法如下：

式中：为归一化之后的数据，x为待优化参数实际值，xmax为待优化参数的最大值，xmin为待优化参数的最小值。

进一步的，步骤3中的目标函数表述为：

f(α,β,γ)＝λ1ηad,av+λ2cd

式中：λ1为涡轮叶片面平均冷却效率权重比；ηad,av为涡轮叶片面平均冷却效率；λ2为扇形孔流量系数权重比；cd为扇形孔流量系数。

进一步的，步骤4所述径向基神经网络表述如下：

径向基神经网络分为三层：输入层，隐藏层，输出层，

隐藏层第i个神经元节点中心的输入值表示为：

hi＝||x-ci||

式中：x＝(x1，x2，…，xk)为网络输入矢量，k表示网络输入的个数，xj表示第j个网络输入，j＝1,2,3...k；ci＝(c1i，c2i，…，cki)为第i个神经元节点的中心，cji表示第j个网络输入的第i个神经元节点的中心；||*||表示欧式范数；

隐藏层第j个神经元节点输出值表示为：

式中：δ表示径向基神经网络扩展速度；

输出层神经元的输出值表示为：

式中：w＝(w1，w2，…，wn)为连接隐藏层和输出层的权值，n表示隐藏层的个数。

进一步的，步骤5所述的径向基神经网络预测目标函数值fobj,pre和测试样本fobj.test误差表述为：

运用试错法，基于大范围扩展速度，得到径向基神经网络预测目标函数值fobj,pre和测试样本fobj.test最小误差。

进一步的，步骤6中粒子群算法优化问题表述为：

maxf(α,β,γ)＝λ1ηad,av+λ2cd

式中：f(α，β，γ)为适应度函数；αmin、αmax参数α对应变化范围最大值和最小值；βmin、βmax参数β对应变化范围最大值和最小值；γmin、γmax参数γ对应变化范围最大值和最小值；

步骤6.1，设置最大迭代次数、粒子群规模、惯性权重、学习因子，初始化粒子及粒子速度；

步骤6.2，粒子适应度检测；

步骤6.3，寻找个体极值和群体极值；

步骤6.4，速度更新和位置更新；

步骤6.5，粒子适应度计算；

步骤6.6，个体极值和群体极值更新；

步骤6.7，判断是否满足终止条件，若不满足，则返回步骤6.4。

进一步的，步骤6.1中惯性权重采用动态变化方法，其公式如下：

w(k)＝wstart-(wstart-wend)(k/nmax)²

式中：k为当前迭代代数，w(k)为当前迭代的惯性权重；wstart为初始惯性权重，wstart＝0.9；wend为迭代至最大次数时的惯性权重，wend＝0.4；nmax为最大迭代代数。

进一步的，步骤7所述的径向基神经网络预测目标函数值fobj,pre和cfd计算目标函数值fobj,cal误差表述为：

有益效果：本发明利用经过实验验证过的cfd模型，基于径向基神经网络(rbfnn)利用训练样本和测试样本进行函数逼近，并耦合粒子群算法全局搜索得到最优设计点，与现有的技术相比，本发明函数逼近基于rbfnn，预测精度高，全局逼近能力强；本发明优化算法基于粒子群算法，为解决可能会陷入局部最小值问题，惯性权重采用动态变化方法；本发明可以进行数据库扩充，以少量的训练样本和测试样本，全局搜索出准确最优设计点；本发明可以根据实际需求，调节气动性能和热性能的权值，设计出兼顾气动性能和热力性能的最优扇形孔的气膜冷却结构；本发明效率高，消耗资源少，可大幅度减少所耗时间和经济成本。

附图说明

图1为涡轮叶片扇形孔气膜冷却结构气动-热协同优化方法流程图；

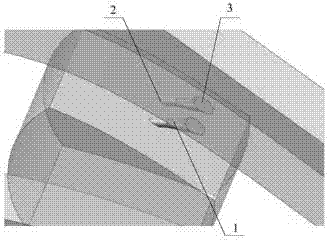
图2为一种涡轮叶片扇形孔气膜冷却几何模型；

图3为扇形孔局部放大图；

图4为扇形孔正视；

图5为扇形孔俯视图；

图6为径向基神经网络结构；

图中标号名称：1.主流入口，2.主流和二次流出口，3.涡轮叶片吸力面，4.涡轮叶片压力面，5.冷气腔，6.扇形孔，7.扇形孔，8.扇形孔冷气入口，9.扇形孔冷气出口。

具体实施方式

下面结合附图对本发明做更进一步的解释。

图1是本发明的一种涡轮叶片扇形孔气膜冷却结构气动-热协同优化方法流程图，下面将参照图1对该方法进行说明。

步骤1，基于图2的涡轮叶片扇形孔气膜冷却几何模型，主流入口速度为140m/s，主流入口温度为540k，扇形气膜孔冷气入口速度为80.4m/s，气膜孔冷气入口温度为310k。

规定扇形孔间距p为4.5d，扇形孔高度h为2.5d，扇形孔前向扩展长度l1为d，扇形孔侧向扩展长度l2为2d，扇形孔圆柱部分长度l3为(h/sinα-3d)。选择涡轮叶片扇形孔倾斜角α，扇形孔侧向扩展角β，扇形孔前向扩展角γ为待优化设计变量，其变化范围分别为25-55°，10-20°，3-15°，其结构图如图3所示。

步骤2，采用拉丁超立方设计方法，对待优化参数涡轮叶片扇形孔倾斜角α，扇形孔侧向扩展角β，扇形孔前向扩展角γ设计25组数据，作为训练样本；对待优化参数涡轮叶片扇形孔倾斜角α，扇形孔侧向扩展角β，扇形孔前向扩展角γ进行随机组合，设计8组数据，作为测试样本。训练样本和测试样本的结构参数如表1所示。

表1

对待优化参数进行归一化处理，归一化处理的方法如下：

式中：为归一化之后的数据，x为待优化参数实际值，xmax为待优化参数的最大值，xmin为待优化参数的最小值。

步骤3，对数据样本建立cfd模型，并计算目标函数值fobj，cal。目标函数表述为：

f(α,β,γ)＝λ1ηad,av+λ2cd

式中：λ1为涡轮叶片面平均冷却效率权重比；ηad,av为涡轮叶片面平均冷却效率；λ2为扇形孔流量系数权重比；cd为扇形孔流量系数。

涡轮叶片面平均冷却效率ηad,av表述为：

式中：d为扇形孔入口圆形直径，ηad,avx为线平均绝热气膜冷却效率。流量系数cd表述为：

式中：m为流经气膜通道的实际流量；a为气膜孔出口冷气通道的横截面积；ρout气膜孔出口处气体的密度，pin^*为气膜孔入口处气体的总压，pout气膜孔出口处气体的静压。

步骤4，利用训练样本和测试样本，训练和测试rbfnn。径向基神经网络结构如图4所示，为三层：输入层，隐藏层，输出层。

隐藏层第i个神经元节点中心的输入值表示为：

hi＝||x-ci||

式中：x＝(x1，x2，…，xk)为网络输入矢量，k表示网络输入的个数，xj表示第j个网络输入，j＝1,2,3...k；ci＝(c1i，c2i，…，cki)为第i个神经元节点的中心，cji表示第j个网络输入的第i个神经元节点的中心；||*||表示欧式范数。

隐藏层第j个神经元节点输出值表示为：

式中：δ表示rbfnn扩展速度。

输出层神经元的输出值表示为：

式中：w＝(w1，w2，…，wn)为连接隐藏层和输出层的权值。

步骤5，输出rbfnn预测目标函数值fobj,pre和测试样本目标函数值fobj.test最小误差下的扩展速度。rbfnn预测目标函数值fobj,pre和测试样本fobj.test误差表述为：

运用试错法，基于大范围扩展速度，得到rbfnn预测目标函数值fobj,pre和测试样本fobj.test最小误差。

步骤6，利用粒子群算法(pso)耦合rbfnn搜索最优设计点。

粒子群算法适应度函数表述为：

maxf(α,β,γ)＝λ1ηad,av+λ2cd

式中：f(α，β，γ)为适应度函数。αmin、αmax参数α对应变化范围最大值和最小值；βmin、βmax参数β对应变化范围最大值和最小值；γmin、γmax参数γ对应变化范围最大值和最小值。

步骤6.1，设置最大迭代次数、粒子群规模、惯性权重、学习因子，初始化粒子及粒子速度；

其中惯性权重采用动态变化方法，其公式如下：

w(k)＝wstart-(wstart-wend)(k/nmax)²

式中：k为当前迭代代数，w(k)为当前迭代的惯性权重；wstart为初始惯性权重，wstart＝0.9；wend为迭代至最大次数时的惯性权重，wend＝0.4；nmax为最大迭代代数。

步骤6.2，粒子适应度检测；

步骤6.3，寻找个体极值和群体极值；

步骤6.4，速度更新和位置更新；

步骤6.5，粒子适应度计算；

步骤6.6，个体极值和群体极值更新；

步骤6.7，判断是否满足终止条件，若不满足，则返回步骤6.4。

步骤7，对优化设计点进行cfd评估，如果rbfnn预测目标函数值fobj,pre与cfd计算目标函数值fobj,cal误差大于5％，则将此优化设计点扩充训练样本数据库，重新从步骤4开始迭代，直到rbfnn预测fobj与cfdfobj误差满足要求，迭代终止，得到全局最优设计点。其中rbfnn预测目标函数值fobj,pre和cfd计算目标函数值fobj,cal误差表述为：

以上所述仅是本发明的优选实施方式，应当指出，对于本技术领域的普通技术人员来说，在不脱离本发明原理的前提下，还可以做出若干改进和润饰，这些改进和润饰也应视为本发明的保护范围。