多自由度梁式结构非线性类型确定方法与流程

本发明涉及对于多自由度梁式结构的非线性类型的判别方法，其判别结果用于评估结构的使用状态和安全性能。

背景技术：

在结构的健康监测中，结构的非线性类型是评价结构安全性的重要指标，也是结构健康监测的关键参数之一。对于非线性结构动力学的研究已有相当一段时间，最早的非线性结构模型识别见于上个世纪70年代，随后，由于不同非线性的特性，各种识别方法相继问世。早期的方法主要针对单自由度结构而言，上个世纪末多自由度集中参数系统的非线性识别得到了发展。目前，对大型结构的复杂非线性系统识别正在研究当中，主要的方法有恢复力曲面法、hilbert变换法和narmax模型识别法等。但是，已有方法在多自由度梁式结构非线性类型识别中存在着方法状态不适应，得到的非线性参数不准确，理论研究结果与实际相差较大等一系列问题。

技术实现要素：

本发明是针对上述现有技术所存在的不足，提供一种多自由度梁式结构非线性类型确定方法，以期能够准确识别多自由度梁式结构的非线性类型，并能得到与实际较相符的非线性模型参数。

本发明为解决技术问题采用如下技术方案：

本发明多自由度梁式结构非线性类型确定方法，所述多自由度梁式结构具有至少两个依次相连的单元，单元节点是指相邻单元之间的连接点；

本发明所述非线性类型的确定方法的特点是按如下步骤进行：

步骤1、对于所述多自由度梁式结构建立结构动力方程；

步骤2、采用动力凝聚法消除所述结构动力方程中的转动自由度，并按照所述多自由度梁式结构的单元边界条件修正所述动力方程，获得修正的结构动力方程；

步骤3、利用所述修正的结构动力方程获得单元相对位移量、单元速度与单元恢复力之间的函数关系；

步骤4、利用所述单元相对位移量、单元速度与单元恢复力之间的函数关系，绘制各单元恢复力曲面和刚度截面曲线；

步骤5、利用所述刚度截面曲线计算各单元的刚度的原始非线性指标；

步骤6、对于所述原始非线性指标进行主元分析，得到降维非线性指标；

步骤7、针对所述降维非线性指标，采用支持向量机分类器判断出各单元的刚度的非线性类型；

步骤8、利用判断出的各单元的刚度的非线性类型，采用最小二乘法确定非线性参数；以此判断各单元是否发生非线性变化，发生了何种非线性变化，进而判断出结构发生非线性变化的位置。

本发明多自由度梁式结构非线性类型确定方法的特点也在于：对于步骤7中所采用的支持向量机分类器按如下方式进行前期数据训练：

确定n种非线性类型，对于每一种非线性类型，在其非线性模型参数范围内选取100组不同的模型参数，将所述模型参数纳入单自由度结构动力方程中，计算获得单自由度结构的结构动力响应，根据所述结构动力响应计算获得单自由度结构原始非线性指标，对于所述单自由度结构原始非线性指标通过主元分析得到单自由度结构降维非线性指标，以所述单自由度结构降维非线性指标作为支持向量机分类器的训练数据，实现支持向量机n种非线性类型的前期数据训练；

所述单自由度结构动力方程为：

其中，m为单自由度结构质量；x、和分别为单自由度结构中单元节点的位移量、速度和加速度响应；为单自由度结构恢复力，所述单自由度结构恢复力的方向是指向平衡位置；f(t)为外部激励。

本发明多自由度梁式结构非线性类型确定方法的特点也在于：所述n种非线性类型包括：线性、双线性刚度、分段线性刚度、三次刚度硬化、二次阻尼和库伦摩擦。

本发明多自由度梁式结构非线性类型确定方法的特点也在于：所述原始非线性指标分别为：

刚度截面曲线与其两端点所连直线包围的面积a1，用于区分线性系统与刚度非线性系统；

刚度截面曲线与其两端点所连直线包围的面积的绝对值a2，用于区分双线性刚度系统与其他刚度非线性系统；

刚度截面曲线与其两端点所连直线各点差值的标准差a3，用于区分刚度非线性系统；

阻尼截面曲线与其两端点所连直线各点差值的标准差a4，用于区分阻尼非线性与其他系统；

阻尼截面曲线速度为零位置处的两侧恢复力差值a5，用于区分二次阻尼和库伦阻尼；

刚度截面曲线左端点斜率a6，用于区分刚度非线性系统；

刚度截面曲线位移为零位置处的左侧斜率a7，用于区分刚度非线性系统；

刚度截面曲线位移为零位置处的右侧斜率a8，用于区分刚度非线性系统；

刚度截面曲线右端点斜率a9，用于区分刚度非线性系统。

本发明多自由度梁式结构非线性类型确定方法的特点也在于：所述步骤2中采用动力凝聚法消除所述结构动力方程中的转动自由度是按如下方法进行：针对多自由度梁式结构中的任意一个单元，在建立其结构动力方程的过程中，按首先纳入其平动自由度，然后再纳入转动自由度的顺序建立单元刚度矩阵k、单元质量矩阵m和单元阻尼矩阵c，分别为：

其中，l为单元长度，ei为抗弯刚度，α和β为瑞利阻尼系数；

则结构动力方程表达为式(1)：

u和θ分别为单元平动位移量和单元转动位移量；和分别为单元平动速度和单元转动速度；和分别为单元平动加速度和单元转动加速度；将式(1)展开，得到式(2)和式(3)：

由式(3)得到式(4)：

将式(4)引入式(2)，获得由式(5)表征的结构动力方程：

其中，mt＝mtt，在式(5)表征的结构动力方程中，只包含有平动自由度，当结构发生非线性变化，其刚度矩阵k发生变化，凝聚后的刚度矩阵kt也发生相应变化。

与已有技术相比，本发明有益效果体现在：

1、本发明充分利用了恢复力曲面和支持向量机的优势，实现多自由度梁式结构的非线性类型的准确识别，并得出与实际较为符合的高精度的非线性模型参数。

2、本发明方法能够在很广的各种函数中集中构造函数，通用性强；

3、本发明方法具有鲁棒性，不需要微调；

4、本发明方法理论完善，方法有效，计算过程简单。

附图说明

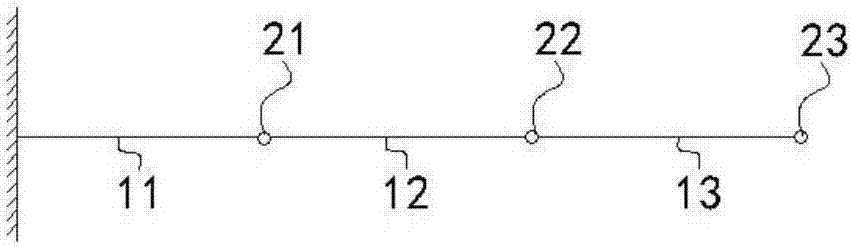
图1为三单元的悬臂梁结构示意图；

图2为三单元的悬臂梁结构所受到的地震加速度；

图3a、图3c和图3e分别为第一节点21、第二节点22和第三节点23的竖向位移示意图；

图3b、图3d和图3f分别为第一节点21、第二节点22和第三节点23的转角位移示意图；

图4a、图4c和图4e分别为第三单元13、第二单元12和第一单元11的相对位置示意图；

图4b、图4d和图4f分别为第三单元13、第二单元12和第一单元11的恢复力示意图；

图5a、图5b和图5c分别为第三单元13、第二单元12和第一单元11的刚度截面曲线；

表1为本发明中涉及的非线性类型及其函数形式；

表2为利用本发明方法实现识别的非线性类型识别结果；

表3为利用本发明方法实现识别的非线性模型参数识别结果。

具体实施方式

本实施例中多自由度梁式结构具有至少两个依次相连的单元，单元节点是指相邻单元之间的连接点。图1为本实施例中三单元悬臂梁，所示包括有第一单元11、第二单元12和第三单元13，并形成有第一节点21、第二节点22和第三节点23。

本实施例中的悬臂梁所受的激励为地震激励，如图2所示为三单元的悬臂梁结构所受到的地震加速度。忽略轴向平动自由度，结构参数如下：模型共分为三个梁单元，忽略轴向平动自由度，结构参数为：质量mi＝4000kg，抗弯刚度ei＝355gpa，惯性矩ii＝0.007m4，i＝1,2,3。结构长15m，每个单元长5m。α取为0.2，β取为1×10-3。

本实施例中多自由度梁式结构非线性类型确定方法是按如下步骤进行：

步骤1、对于多自由度梁式结构建立如式(6)所示的结构动力方程：

式(6)中，x、和分别表示结构各自由度的位移、速度和加速度；m、k、c分别为结构质量矩阵、刚度矩阵和阻尼矩阵，f(t)为外部激励，t为时间。

将本实施例中需要进行判别的图1所示结构的实际m、k、c、f(t)代入式(6)，得到针对这一实际结构的动力方程。

c＝0.2×m+1×10-3×k；

外部激励见图2，图2表示三单元悬臂结构受到的地震加速度。

步骤2、按如下方式，采用动力凝聚法消除结构动力方程中的转动自由度，并按照多自由度梁式结构的单元边界条件修正动力方程，获得修正的结构动力方程如式(5)。

针对多自由度梁式结构中的任意一个单元，在建立其结构动力方程的过程中，按首先纳入其平动自由度，然后再纳入转动自由度的顺序建立单元刚度矩阵k、单元质量矩阵m和单元阻尼矩阵c，分别为：

l为单元长度，ei为抗弯刚度，α和β为瑞利阻尼系数，则结构动力方程表达为式(1)：

u和θ分别为单元平动位移量和单元转动位移量；和分别为单元平动速度和单元转动速度；和分别为单元平动加速度和单元转动加速度；

将式(1)展开，得到式(2)和式(3)：

由式(3)得到式(4)：

将式(4)引入式(2)，获得由式(5)表征的结构动力方程：

其中，mt＝mtt，在式(5)表征的结构动力方程中，只包含有平动自由度，当结构发生非线性变化，其刚度矩阵k发生变化，凝聚后的刚度矩阵kt也发生相应变化。

如此，结构动力方程中即消除了转动自由度的影响，只有平动自由度。避免了在结构动力方程中既考虑平动又考虑转动带来的复杂性，使计算只归结于对平动的考虑，降低难度。

步骤3、利用修正的结构动力方程获得单元相对位移量、单元速度与单元恢复力之间的函数关系；

图3a、图3c和图3e分别为第一节点21、第二节点22和第三节点23的竖向位移示意图；图3b、图3d和图3f分别为第一节点21、第二节点22和第三节点23的转角位移示意图。图中示出各节点在地震激励作用下发生了较为激烈的振动，偏离中心位置较多，转角较大。

图4a、图4c和图4e分别为第三单元13、第二单元12和第一单元11的相对位置示意图；图4b、图4d和图4f分别为第三单元13、第二单元12和第一单元11的恢复力示意图。图中所示的相对位移的变化幅度较大；各个时刻的各个单元的恢复力在图像中可以清晰地得出。

步骤4、利用单元相对位移量、单元速度与单元恢复力之间的函数关系，绘制各单元恢复力曲面和刚度截面曲线；在单元相对位移量、单元速度与单元恢复力之间的函数关系式基本确定之后，每一个采样时刻的三维数值点便可确定，通过插值可得单元的恢复力曲面。在恢复力曲面求得的情况下，恢复力曲面位移方向的截面曲线即为刚度截面曲线，恢复力曲面速度方向的截面曲线即为阻尼截面曲线；故刚度截面曲线与阻尼截面曲线均可求得。

图5a、图5b和图5c分别为第三单元13、第二单元12和第一单元11的刚度截面曲线。如图中示出，刚度截面曲线是由多段折线所组成，是建立在修正之后的结构动力方程的基础上，是对单元相对位移量、单元速度、单元恢复力三者之间关系的图像表达。

步骤5、利用刚度截面曲线计算各单元的刚度的原始非线性指标；根据各个原始非线性指标的定义，由图5a、图5b和图5c可以求出原始非线性指标。

步骤6、对于原始非线性指标进行主元分析，得到降维非线性指标；主元分析是多元统计理论中的经典方法，主要用于在最小二乘意义上寻求一种线形变换将高维变量转换到低维空间中去，广泛运用于故障诊断和损伤识别中。其本质意义在于寻找一种新变量来代替原变量，而此时的新变量是原变量的线性组合。本实施例将主元分析的算法运用到结构的非线性模型检验及参数确定中，用于处理计算得到的原始非线性指标，将原始非线性的维数降低到可方便计算的范围之内，降维非线性指标。

步骤7、针对降维非线性指标，采用支持向量机分类器判断出各单元的刚度的非线性类型；支持向量机是一种基于统计学习理论的模式识别方法，是建立一个分类超平面作为决策曲面，使得正例和反例之间的隔离边缘被最大化。用分类向量机做分类预测时需要调整相关的参数，主要是惩罚参数c和核函数参数g，如此才能得到比较理想的预测分类准确率。但如何选取最优参数，目前还没有公认的最好的方法。常见的方法是让c和g在一定的范围内取值，对每一组取定的c和g都要进行准确率计算，最后选取准确率最高的那一组参数。但是这样选取比较费时，本实施例采用的是遗传算法寻优的方法，把对训练集进行cv意义下的准确率作为遗传算法的适应度函数值，对支持向量机参数进行优化。

非线性类型及其函数形式见表1，表1也给出了各种非线性参数的取值范围。其中表1中的k，kn1，kn2，kn均表示各种非线性下的刚度系数；c为阻尼；d为分段线性刚度的临界长度；b为库仑力；a为单位阻尼系数。由表2可以看出支持向量机分类器得到的三个单元的非线性类型，单元一发生了分段线性刚度；单元二和单元三非线性的类型为线形。

本实施例中，对于支持向量机分类器是按如下方式进行前期数据训练：

确定n种非线性类型，对于每一种非线性类型，在其非线性模型参数范围内选取100组不同的模型参数，将模型参数纳入单自由度结构动力方程中，计算获得单自由度结构的结构动力响应，根据结构动力响应计算获得单自由度结构原始非线性指标，对于单自由度结构原始非线性指标通过主元分析得到单自由度结构降维非线性指标，以单自由度结构降维非线性指标作为支持向量机分类器的训练数据，实现支持向量机n种非线性类型的前期数据训练；

单自由度结构动力方程为：其中：m为单自由度结构质量；x、和分别为单自由度结构中单元节点的位移量、速度和加速度响应；为单自由度结构恢复力，单自由度结构恢复力的方向是指向平衡位置；f(t)为外部激励；n种非线性类型包括：线性、双线性刚度、分段线性刚度、三次刚度硬化、二次阻尼和库伦摩擦。

本实施例中所指的原始非线性指标分别为：

刚度截面曲线与其两端点所连直线包围的面积a1，用于区分线性系统与刚度非线性系统；

刚度截面曲线与其两端点所连直线包围的面积的绝对值a2，用于区分双线性刚度系统与其他刚度非线性系统；

刚度截面曲线与其两端点所连直线各点差值的标准差a3，用于区分刚度非线性系统；

阻尼截面曲线与其两端点所连直线各点差值的标准差a4，用于区分阻尼非线性与其他系统；

阻尼截面曲线速度为零位置处的两侧恢复力差值a5，用于区分二次阻尼和库伦阻尼；

刚度截面曲线左端点斜率a6，用于区分刚度非线性系统；

刚度截面曲线位移为零位置处的左侧斜率a7，用于区分刚度非线性系统；

刚度截面曲线位移为零位置处的右侧斜率a8，用于区分刚度非线性系统；

刚度截面曲线右端点斜率a9，用于区分刚度非线性系统。

步骤8、利用判断出的各单元的刚度的非线性类型，采用最小二乘法确定非线性参数；如表3所示，分别获得了三个单元的刚度非线性模型参数。与理论值相比较，可以看出该方法识别的精度很高；至此即判断出各单元是否发生了非线性变化，发生了何种非线性变化，进而判断出结构发生非线性变化的位置。

表1非线性类型及其函数形式

表2非线性类型识别结果

表3非线性模型参数识别结果

本发明方法能够在很广的各种函数中集中构造函数，通用性强；其理论完善，方法有效，计算过程简单。