一种高峰时段多列车节能优化方法与流程

本发明属于列车运行控制技术领域，特别是一种高峰时段多列车节能优化方法。

背景技术：

近年来，随着国民经济快速持续发展、城市化进程的快速推进以及我国城市轨道交通的快速发展及多条线路的开通运行，城市轨道交通能耗也越来越大。因此，城市轨道交通的节能对我国环境保护和能源节约具有重大意义。

目前国内外对再生制动能量的研究主要有三种方向，第一种研究方向是安装车载或地面能量吸收装置，包括蓄电池、飞轮、超级电容等设备，以储存列车再生制动产生的能量，供牵引状态的列车使用。第二种研究方向是对逆变回馈装置的设计与研制。第三种研究方向是通过优化时刻表，使同一个牵引区间运行的相邻列车牵引和再生制动过程相重叠，以提高系统再生制动能量的利用效率，降低牵引区间总能量。从运营角度上看，储能装置和逆变回馈装置的设计、制造以及安装维护成本比较高，相比前者，优化时刻表是一种既经济又具有实际应用价值的研究方向。

技术实现要素：

本发明的目的在于提供一种高峰时段多列车节能优化方法，通过优化时刻表，使同一个牵引区间运行的相邻列车牵引和再生制动过程相重叠，以提高系统再生制动能量的利用效率，降低牵引区间总能量。

实现本发明目的的技术解决方案为：一种高峰时段多列车节能优化方法，包括以下步骤：

步骤1，初始化多列车优化运行的基本数据以及仿真时间；基本数据包括线路数据、列车数据、运营数据以及与遗传算法相关的基本参数；

步骤2，以列车牵引能耗和区间旅行时间为优化目标，建立高峰时段多列车节能优化模型；

步骤3，利用pareto多目标遗传算法，求解高峰时段多列车节能优化模型，得到一组列车运行策略的非支配解集；

步骤4，提取全局最优解，求出优化后的时刻表，完成高峰时段多列车节能优化模型的求解。

进一步地，步骤1中所述的线路数据包括车站配置、坡度、曲率半径和临时限速数据；所述的列车数据包括列车型号、车长、编组方式、载荷情况、牵引特性曲线和制动特性曲线；所述的运营数据包括各站停站时间、发车间隔、单位小时发车对数和区间运行时间；所述的与遗传算法相关的基本参数包括选择算子、交叉算子、变异算子、最大进化代数、种群大小和适应度函数。

进一步地，步骤2中所述的以列车牵引能耗和区间旅行时间为优化目标，建立高峰时段多列车节能优化模型，具体如下：

与重叠时间相关的目标函数f1(x)为

与列车总运行时间相关的目标函数f2(x)为

与总运行时间相关的约束条件g1(x)为

与停站时间相关的约束条件g2(x)为

ldi≤g2(x)＝dn≤udi(4)

与发车间隔相关的约束条件g3(x)为

lh≤g3(x)＝hi(5)

式中：m为牵引供电区间的总数；n为单向高峰时段单位小时发出的列车总数；hi为列车i的发车间隔；dn为列车在车站n的停站时间；dk为列车在车站k的停站时间，tj为列车在区间j的运行时间；ldi、udi分别为最小停站时间和最大停站时间值；lh为最小发车间隔时间。

进一步地，步骤3所述利用pareto多目标遗传算法，求解高峰时段多列车节能优化模型，得到一组列车运行策略的非支配解集，具体如下：

步骤3.1、初始化种群p，种群大小为n，种群中每个个体对应一组停站时间矩阵xi＝[d1,d2,...dj,...,dk]，k表示车站数；各站的停站时间采用整数编码，列车在上下行同一车站的停站时间相同；

步骤3.2、首先根据种群中每个个体对应的停站时间染色体编码矩阵xi和发车间隔时间hi，计算出种群中每个个体对应的时刻表，进而求出每辆列车在所有供电区间的重叠时间，最终求出仿真时间段内重叠时间适应度值f1(x)及总运行时间f2(x)，然后对种群中每个个体的节能指标f1(x)和准时指标f2(x)适应度值进行非支配排序，确定种群中每个个体的非支配序值，接着对非支配层中的每个个体进行拥挤度计算，确定种群中非支配次序关系以及个体的拥挤度，最后根据种群中非支配次序关系以及个体的拥挤度，通过锦标赛法从种群p中随机选择个体进行交叉和变异操作，产生子代种群q；

步骤3.3、从第二代开始，首先将父代种群p与子代种群q合并，形成新种群r，种群大小为2n，然后进行非支配排序，确定种群中每个个体的非支配序值，最后对非支配层中的每个个体进行拥挤度计算，根据非支配次序关系以及个体的拥挤度选取合适的个体组成下一代父代种群p，保持种群个体数为n；

步骤3.4、循环步骤3.2～3.3直至达到最大迭代次数，停止遗传操作并保存得到pareto最优的非支配解集。

进一步地，步骤4中所述的提取全局最优解，求出优化后的时刻表，完成高峰时段多列车节能优化模型的求解，具体为：在pareto非支配解集中按制定的节能和准时的相对优先级别选择最合适的停站时间矩阵作为全局最优解，求出优化后的时刻表，完成高峰时段多列车节能优化模型的求解。

本发明与现有技术相比，其显著优点为：(1)基于pareto多目标遗传算法的高峰时段多列车节能优化运行方法，在搜索过程中不易陷入局部最优，进化结果不局限于单值解，非常适合求解复杂的多目标问题；(2)通过选择、交叉、变异操作来表现复杂现象，充分利用适应值函数而不需要其它先验知识，提高系统再生制动能量的利用效率，降低牵引区间总能量。

附图说明

图1是本发明高峰时段多列车节能优化方法的流程图。

图2是本发明pareto多目标遗传算法的流程图。

图3是本发明中7:00-8:00列车运行图。

图4是本发明中优化前后每列车重叠时间对比图。

具体实施方式

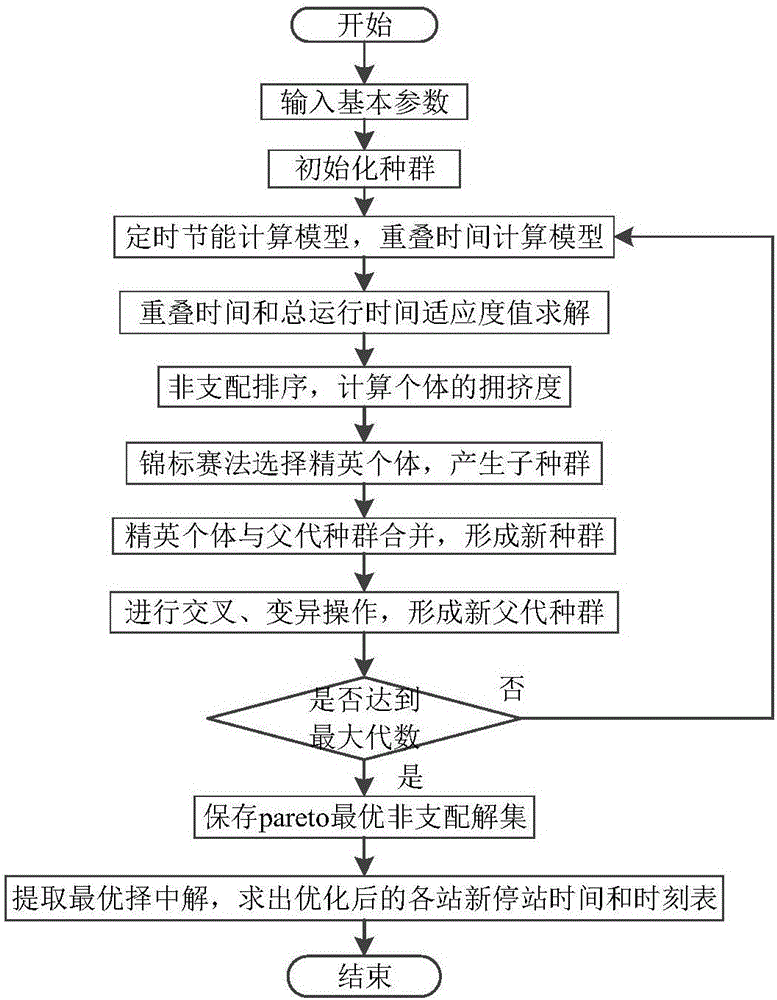
结合图1，本发明高峰时段多列车节能优化方法，包括以下步骤：

步骤1，初始化多列车优化运行的基本数据以及仿真时间；基本数据包括线路数据、列车数据、运营数据以及与遗传算法相关的基本参数；

步骤2，以列车牵引能耗和区间旅行时间为优化目标，建立高峰时段多列车节能优化模型；

步骤3，利用pareto多目标遗传算法，求解高峰时段多列车节能优化模型，得到一组列车运行策略的非支配解集；

步骤4，提取全局最优解，求出优化后的时刻表，完成高峰时段多列车节能优化模型的求解。

进一步地，步骤1中所述的线路数据包括车站配置、坡度、曲率半径和临时限速数据；所述的列车数据包括列车型号、车长、编组方式、载荷情况、牵引特性曲线和制动特性曲线；所述的运营数据包括各站停站时间、发车间隔、单位小时发车对数和区间运行时间；所述的与遗传算法相关的基本参数包括选择算子、交叉算子、变异算子、最大进化代数、种群大小和适应度函数。

进一步地，步骤2中所述的以列车牵引能耗和区间旅行时间为优化目标，建立高峰时段多列车节能优化模型，具体如下：

与重叠时间相关的目标函数f1(x)为

与列车总运行时间相关的目标函数f2(x)为

与总运行时间相关的约束条件g1(x)为

与停站时间相关的约束条件g2(x)为

ldi≤g2(x)＝dn≤udi(4)

与发车间隔相关的约束条件g3(x)为

lh≤g3(x)＝hi(5)

式中：m为牵引供电区间的总数；n为单向高峰时段单位小时发出的列车总数；hi为列车i的发车间隔；dn为列车在车站n的停站时间；dk为列车在车站k的停站时间，tj为列车在区间j的运行时间；ldi、udi分别为最小停站时间和最大停站时间值；lh为最小发车间隔时间。

进一步地，步骤3所述利用pareto多目标遗传算法，求解高峰时段多列车节能优化模型，得到一组列车运行策略的非支配解集，结合图2，具体如下：

步骤3.1、初始化种群p，种群大小为n，种群中每个个体对应一组停站时间矩阵xi＝[d1,d2,...dj,...,dk]，k表示车站数；各站的停站时间采用整数编码，列车在上下行同一车站的停站时间相同；

步骤3.2、首先根据种群中每个个体对应的停站时间染色体编码矩阵xi和发车间隔时间hi，计算出种群中每个个体对应的时刻表，进而求出每辆列车在所有供电区间的重叠时间，最终求出仿真时间段内重叠时间适应度值f1(x)及总运行时间f2(x)，然后对种群中每个个体的节能指标f1(x)和准时指标f2(x)适应度值进行非支配排序，确定种群中每个个体的非支配序值，接着对非支配层中的每个个体进行拥挤度计算，确定种群中非支配次序关系以及个体的拥挤度，最后根据种群中非支配次序关系以及个体的拥挤度，通过锦标赛法从种群p中随机选择个体进行交叉和变异操作，产生子代种群q；

步骤3.3、从第二代开始，首先将父代种群p与子代种群q合并，形成新种群r，种群大小为2n，然后进行非支配排序，确定种群中每个个体的非支配序值，最后对非支配层中的每个个体进行拥挤度计算，根据非支配次序关系以及个体的拥挤度选取合适的个体组成下一代父代种群p，保持种群个体数为n；

步骤3.4、循环步骤3.2～3.3直至达到最大迭代次数，停止遗传操作并保存得到pareto最优的非支配解集。

进一步地，步骤4中所述的提取全局最优解，求出优化后的时刻表，完成高峰时段多列车节能优化模型的求解，具体为：在pareto非支配解集中按制定的节能和准时的相对优先级别选择最合适的停站时间矩阵作为全局最优解，求出优化后的时刻表，完成高峰时段多列车节能优化模型的求解。

实施例1

结合图1～4，一种高峰时段多列车节能优化方法，包括以下步骤：

步骤1，以广州地铁七号线广州南站至大学城南站(上行方向)数据进行仿真分析，选择的高峰时段为：初期7:00至8:00。按照牵引配电站供电范围划分，将供电范围分为6段，即广州南站-谢村站、谢村站-钟村站、钟村站-鹤庄站、鹤庄站-官堂站以及官堂站-南村站。初始化多列车优化运行的基本数据以及仿真时间，基本数据主要包括线路数据、列车数据、运营数据以及与遗传算法相关的基本参数，其中，线路数据包括车站配置、坡度、曲率半径和临时限速数据；列车数据包括列车型号、车长、编组方式、载荷情况、牵引特性曲线和制动特性曲线；运营数据包括各站停站时间、发车间隔、单位小时发车对数和区间运行时间；与遗传算法相关的基本参数包括选择算子、交叉算子、变异算子、最大进化代数、种群大小和适应度函数；

步骤2，以列车牵引能耗和区间旅行时间为优化目标，建立高峰时段多列车节能优化模型，高峰时段多列车节能优化模型为：

与重叠时间相关的目标函数f1(x)为

与列车总运行时间相关的目标函数f2(x)为

与总运行时间相关的约束条件g1(x)为

与停站时间相关的约束条件g2(x)为

ldi≤g2(x)＝dn≤udi(4)

与发车间隔相关的约束条件g3(x)为

lh≤g3(x)＝hi(5)

式中：m为牵引供电区间的总数；n为单向高峰时段单位小时发出的列车总数；hi为列车i的发车间隔；dn为列车在车站n的停站时间；dk为列车在车站k的停站时间，tj为列车在区间j的运行时间；ldi、udi分别为最小停站时间和最大停站时间值；lh为最小发车间隔时间；

步骤3，利用pareto多目标遗传算法求解高峰时段多列车节能优化模型，得到一组列车运行策略的非支配解集；

求解该优化模型的过程包括如下子步骤：

3.1初始化种群p，种群大小为n，种群中每个个体对应一组停站时间矩阵xi＝[d1,d2,...dj,...,dk]，k表示车站数，各站的停站时间采用整数编码，列车在上下行同一车站的停站时间相同；

3.2首先根据种群中每个个体对应的停站时间染色体编码矩阵xi和发车间隔时间hi，计算出种群中每个个体对应的时刻表；进而求得每辆列车在所有供电区间的重叠时间，最终求得仿真时间段内重叠时间适应度值f1(x)及总运行时间f2(x)，对种群中每个个体的节能指标f1(x)和准时指标f2(x)适应度值进行非支配排序，确定种群中每个个体的非支配序值，然后对非支配层中的每个个体进行拥挤度计算，确定种群中非支配次序关系以及个体的拥挤度，根据种群中非支配次序关系以及个体的拥挤度，通过锦标赛法从种群p中随机选择个体进行交叉和变异操作，产生子代种群q；

3.3从第二代开始，首先将父代种群p与子代种群q合并，形成新种群r，种群大小为2n，其次进行非支配排序，确定种群中每个个体的非支配序值，然后对非支配层中的每个个体进行拥挤度计算，根据非支配次序关系以及个体的拥挤度选取合适的个体组成下一代父代种群p，保持种群个体数为n；

3.4通过遗传算法的选择、交叉和变异操作产生新的子代种群，依此类推，直到满足结束条件，停止遗传操作，并保存pareto前沿的非支配解集；

步骤4，提取全局最优解，在pareto非支配解集中按制定的节能和准时的相对重要性选择最合适的停站时间矩阵作为全局最优解，然后求出优化后的时刻表，完成高峰时段多列车节能优化模型的求解，得到7:00至8:00优化后的列车运行图，如图3所示，以及随着发车间隔的增加，优化前后平均每列车的重叠时间都相应减少，而发车间隔较小时重叠时间的优化相比发车间隔较大时重叠时间的优化效果更趋于稳定，如图4所示。