一种利用截面法确定车辆转向节回转半径的方法与流程

本发明涉及一种汽车建模及测量技术，特别涉及一种利用截面法确定车辆转向节回转半径的方法。

背景技术：

目前确定车辆转向节回转半径有如下几种方法：

1)纸上作图法：根据画法几何理论在图纸上模拟转向节的运动，确定转向节回转半径。该方法直观性强，但是精度差，效率低。

2)函数法：建立转向节回转半径计算的数学模型，代入初始条件计算。此方法建模费时，效率低，易出错，直观性差，但是精度高。

3)cae软件法：利用cae软件代入初始条件进行自动计算。此方法的特点是学习cae软件费时，直观性差，易出错，精度高。

技术实现要素：

本发明的目的，在于提供一种利用截面法确定车辆转向节回转半径的方法，其采用autocad软件根据投影理论建立二维模型，直观性强，效率高，精度高。

为了达成上述目的，本发明的解决方案是：

一种利用截面法确定车辆转向节回转半径的方法，包括如下步骤：

步骤1，建立转向系统结构模型；

步骤2，建立满载工况右转向拉杆-转向节几何模型；

步骤3，建立满载工况右转向节回转运动模型；

所述步骤3中，根据转向节运动规律，建立转向节回转中心点到球铰中心的连线，其中，转向节回转中心点通过如下方法得到：设ab表示转向节，且b点为球铰中心，用通过b点的两条相交直线l2、l3表示过b点的斜面k，转向时b点在斜面k上绕主销中心线l1转动；通过a点作侧平面，求其与斜面k交线，称为截交线l4；通过a点作截面，该截面既是侧垂面，还垂直于l3，求其与斜面k交线，称为截交线l5；从而求得转向节回转中心点g点；

步骤4，确定转向节回转半径。

上述步骤1的详细内容是：根据三视图理论、转向系统的功能和性能要求，按照适当比例绘制转向系统结构的cad模型，设计并表达转向系统零件几何形状、尺寸、位置和相互联接关系。

上述步骤2中，对右转向拉杆和转向节进行投影，绘制投影三视图，其中，用ab表示转向节，且b点为球铰中心，tb表示右转向拉杆，将a、b、t三点在主视图、俯视图、左视图进行投影，得到投影点。

上述步骤4中，利用转向节回转中心点到球铰中心的连线的投影求其实长，即转向节回转半径。

采用上述方案后，本发明具有以下改进：

(1)本发明提出了一种建立转向节回转运动二维模型的方法，模拟转向运动，采用autocad软件建立转向系统满载工况右转向拉杆-转向节几何模型和右转向节回转运动模型，为计算转向节回转半径奠定基础；

(2)本发明提出了求主销中心线l1与斜面k交点g的方法，称为“截面法”，该方法根据投影理论，作截面，求截交线l4和l5，从而获得交点g，直观性强，效率高，求解精度高。

附图说明

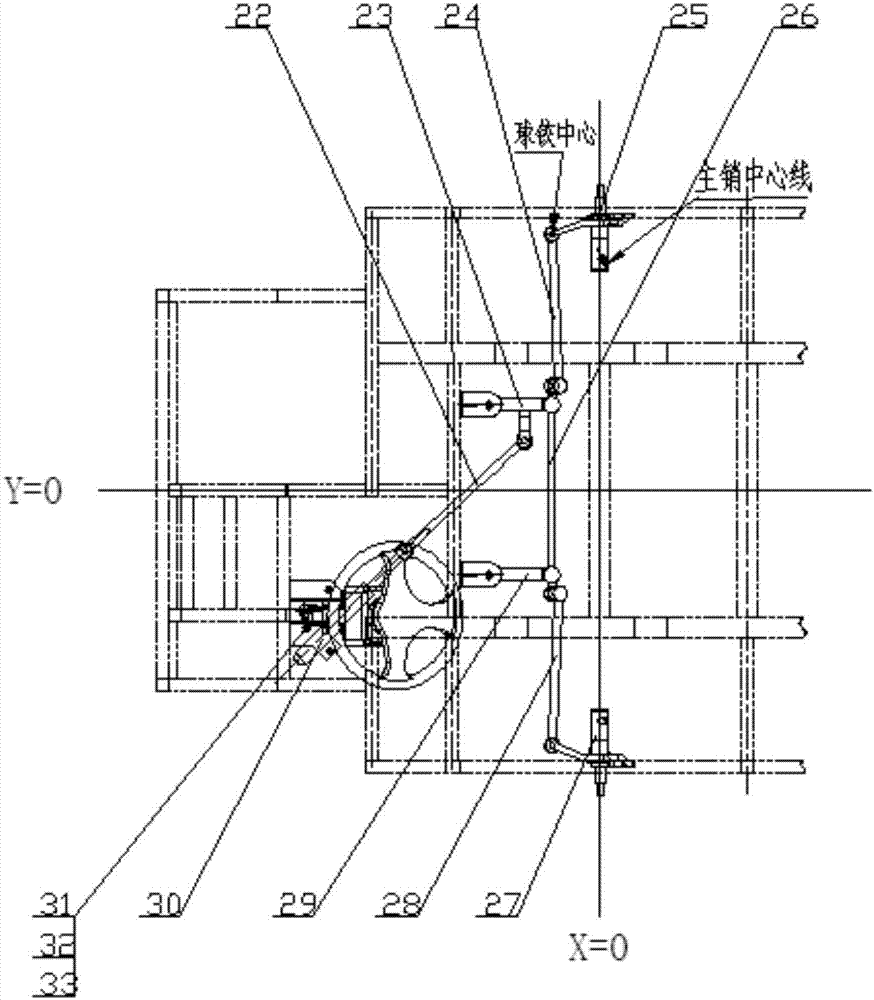
图1是绘制的车辆转向系统结构模型图；

其中，图1a是主视图，图1b是俯视图，图1c是左视图；

1-方向盘传动管柱，2-管柱锁紧螺母，3-方向盘上托架，4-方向盘下托架，5-螺栓，6-螺母，7-垫片，8-方向盘，9-方向盘锁紧螺母，10-锁芯，11-方向盘管柱壳，12-方向盘管柱，13-管柱锁紧螺母，14-花键转换器，15-方向机齿条拉杆销，16-齿条拉杆螺母，17-齿条拉杆垫片，18-转向摇臂支架销，19-摇臂支架销螺母，20-摇臂支架销垫片，21-转向摇臂支架，22-方向机齿条拉杆，23-右转向摇臂，24-右转向拉杆，25-右转向节，26-转向横拉杆，27-左转向节，28-左转向拉杆，29-左转向摇臂，30-方向机支架，31-方向机支架螺栓，32-方向机支架螺母，33-方向机支架垫片；

图2是满载工况右转向拉杆-转向节几何模型图，反映右转向拉杆24与右转向节25之间的几何联接关系；

其中，图2a是主视图，图2b是左视图，图2c是俯视图；

图3是满载工况右转向节回转模型图；

其中，a)为主视图，b)为左视图。

具体实施方式

以下将结合附图，对本发明的技术方案及有益效果进行详细说明。

本发明提供一种利用截面法确定车辆转向节回转半径的方法，包括如下步骤：

步骤1，建立转向系统结构模型

根据三视图理论、转向系统的功能和性能要求，按照适当比例绘制转向系统结构的cad模型，设计并表达转向系统零件几何形状、尺寸、位置和相互联接关系，可配合图1所示。

在图1中，主销中心线为右转向节25在右转向拉杆24推拉下转动的中心线，球铰中心为右转向节25和右转向拉杆24联接处的球铰链中心。

转向系统工作过程如下：驾驶员手驱动方向盘8使转向系统输入功率、圆周运动和扭矩，方向盘8将运动和扭矩传递给方向盘管柱12，方向盘管柱12再将运动和扭矩传递给方向盘传动管柱1，方向盘传动管柱1随之将运动和扭矩传递给花键转换器14，花键转换器14通过方向机将运动和扭矩传递给方向机齿条拉杆22，方向机齿条拉杆22将运动和扭矩传递给右转向摇臂23，右转向摇臂23通过销将运动和扭矩传递给转向横拉杆26，转向横拉杆26通过球铰链将运动和扭矩同时传递给右转向拉杆24和左转向拉杆28，右转向拉杆24最后通过球铰链将运动和扭矩传递给右转向节25及右转向轮，左转向拉杆28最后通过球铰链将运动和扭矩传递给左转向节27及左转向轮，左右转向轮同时运动实现汽车转向。

转向节回转运动过程如下：右转向节25在右转向拉杆24的拉动下绕主销中心线回转，驱动固定在转向节上的车轮转向。

步骤2，建立满载工况右转向拉杆-转向节几何模型

根据前述图1的尺寸和投影理论，对右转向拉杆和转向节进行几何简化，用l1表示右轮主销中心线，ab线(l2)表示转向节，用tb线(l3)表示右转向拉杆。b表示球铰中心，t点表示右转向拉杆24内端球铰中心，a点表示右轮中心线与右轮主销中心线交点，绘制投影三视图如图2，反映了右转向拉杆24与转向节25之间的几何联接关系。

在图2中，x,y,z为坐标轴，坐标原点为o，箭头所指为正方向。a1、a2、a3分别为a点在主视图、俯视图和左视图中的投影点。b1、b2、b3分别为b点在主视图、俯视图和左视图中的投影点。t1、t2、t3分别为t点在主视图、俯视图和左视图中的投影点。α(°)为主销中心线后倾角，顺时针为正；β(°)为主销中心线内倾角，顺时针为正。

步骤3，建立满载工况右转向节回转运动模型

在图2的基础上，根据转向时转向节ab绕主销中心线l1转动的运动规律，用通过b点的l2、l3两条相交直线表示过b点的斜面k，转向时b点在斜面k上绕主销中心线l1转动；求截交线l4，通过a点作截面(平行于yoz投影平面，称为侧平面)，求其与斜面k交线，称为l4；求截交线l5，通过a点作截面既垂直于yoz投影平面(称为侧垂面)，还垂直于l3，求其与斜面k交线，称为l5；从而求g点。本发明称为截面法。

建立右转向节回转运动模型如图3所示。

在图3中，l1、β、α同前，m1、m3分别为m点在主视图和左视图上的投影点，n1、n3分别为n点在主视图和左视图上的投影点，j1、j3分别为j点在主视图和左视图上的投影点，g1、g3分别为g点在主视图和左视图上投影点，a1、a3，b1、b3同前。

图3中m为l2和l4的交点，n为l4和l5的垂直相交点。j为l5与l3交点。g为l1与l5的交点，表示主销中心线l1与斜面k交点。

图3中bg为转向节回转中心点g到球铰中心b的连线。

步骤4，确定转向节回转半径

根据投影理论，利用图3上bg线的投影求其实长，bg线实长就是转向节回转半径。

本发明可应用于汽车转向系统设计和其他机械系统设计的运动分析中，本实施例给出应用案例如表1所示，参数同前。

表1某车辆转向节回转半径计算方案与结果

以上实施例仅为说明本发明的技术思想，不能以此限定本发明的保护范围，凡是按照本发明提出的技术思想，在技术方案基础上所做的任何改动，均落入本发明保护范围之内。