基于直流输电的低速齿轮箱双馈型风电机组优化设计方法与流程

本发明涉及一种优化设计方法，尤其是一种基于直流输电的低速齿轮箱双馈型风电机组优化设计方法，属于风力发电技术领域。

背景技术：

双馈型风力发电系统主要由风力机、齿轮箱、双馈型风力发电机(dfig)、变流器等构成。dfig是一个高速、体积小的发电机，由于风力机低转速运行，因此通常采用高增速比的增速齿轮箱把较低的风力机转速提升到高速的转子转速。齿轮箱的增速比越高，dfig的体积和成本越小；但齿轮箱增速比越大，齿轮箱的体积、成本越高，能量损耗、故障率越大，使整机系统的可靠性越差。双馈型风力发电系统的主要损耗来源于齿轮箱和变流器系统，其中每年大约有65％左右的系统损耗来源于齿轮箱。因此，有必要研究采用低增速比的齿轮箱，以期降低系统的成本、损耗，提高系统运行的可靠性。但传统的dfig定子通常直接与交流电网相连，dfig必须采用恒压恒频运行机制，以确保定子的频率与电网频率一致，因而无法采用低增速比的齿轮箱。

目前直流输电技术因其具有运行可靠、远距离、成本低、损耗小等诸多优势而深受关注，成为连接远距离大规模风电场和电网的理想技术，广泛应用于风力发电输电系统中。实用新型专利zl201420171452.1公开了一种用于柔性直流输电系统的双馈型风电机组变流器拓扑结构，该变流器包括定子侧变流器、机侧变流器、网侧dc-dc变换器，可以直接将双馈型风力发电机输出功率接入直流电网，其中定子侧变流器与dfig的定子连接，实现整流，也就是说dfig的定子不与交流电网连接，因而定子的输出电压和频率无需恒压恒频，变流器可灵活调节定子频率和定子电压，这使得定子的频率可以低于电网频率(如50hz)，因此发电机的同步转速可以降低，从而可采用低增速比的齿轮箱。但齿轮箱增速比降低、同步转速下降将会导致dfig定子、转子电流增大，齿轮箱体积、成本上升，为此必须解决由此带来的全系统优化设计及控制问题。

技术实现要素：

本发明的主要目的在于：针对现有技术的不足和空白，根据柔性直流输电系统的特点，提出一种通过选择最佳齿轮箱变速比对双馈型风电机组进行优化设计方法，以降低齿轮箱增速比、降低双馈型风力发电机组成本、提高系统可靠性。

为了达到以上目的，本发明一种基于直流输电的低速齿轮箱双馈型风电机组优化设计方法，采用一种基于直流输电的双馈型风力发电系统拓扑结构对双馈型风电机组进行优化设计及控制，所述双馈型风力发电系统包括风力机、齿轮箱、双馈型风力发电机、直流变流器、直流母线，所述直流变流器包括定子侧变流器和转子侧变流器，所述双馈型风电机组包括所述齿轮箱、所述双馈型风力发电机和所述直流变流器，其特征在于，包括以下步骤：

步骤1，假设优化前后所述风力机的功率不变，所述双馈型风力发电机的极对数及其定子的感抗、转子的感抗和定转子之间的互感保持不变，定子磁通保持不变，令：

λ＝m/n(1)

式中，n、m分别为优化前所述齿轮箱的增速比和优化后所述齿轮箱的增速比，且m<n，λ为优化后所述齿轮箱的增速比与优化前所述齿轮箱的增速比之比；

采用定子磁通矢量定向控制策略，求优化前后所述双馈型风力发电机的定子电流、转子电流、总电流和所述直流变流器的总电流之比，其计算公式分别为：

式中，is1、isd1、isq1、ir1、it1分别为优化前所述双馈型风力发电机的定子电流、定子电流d轴分量、定子电流q轴分量、转子电流、总电流，ic1为优化前所述直流变流器的总电流；is2、isd2、isq2、ir2、it2分别为优化后所述双馈型风力发电机的定子电流、定子电流d轴分量、定子电流q轴分量、转子电流、总电流，ic2为优化后所述直流变流器的总电流；β为所述双馈型风力发电机的定子自感ls与定转子互感lm的比值，即β＝ls/lm；α＝ird1/isq1。

步骤2，建立优化后所述双馈型风电机组的总成本的计算模型；其计算模型为：

式中，cs2为优化后所述双馈型风电机组的总成本，ct1、cg1、cc1分别为优化前所述双馈型风力发电机的成本、所述齿轮箱的成本、所述直流变流器的成本，k0、k1、k2、k3分别为所述齿轮箱的成本曲线的拟合系数。

步骤3，根据步骤2中所述计算模型求所述双馈型风电机组的优化设计参数，具体包括以下步骤：

1)以λ为横坐标、成本为纵坐标，根据式(6)绘制曲线，求得所述双馈型风电机组的总成本cs2的最小值cs2min，即优化后所述双馈型风电机组的最优成本，与之对应的λ即为最优齿轮箱增速比之比λopt；

2)将λ＝λopt代入式(1)，求得优化后所述齿轮箱的增速比m＝λoptn；

3)将λ＝λopt分别代入式(2)、(3)，获得优化后所述双馈型风力发电机的定子电流is2和转子电流ir2分别为：

4)根据优化后与优化前所述双馈型风力发电机的同步转速之比：

式中，n1n、n1m分别为优化前、优化后的所述双馈型风力发电机的同步转速，ωm1、ωm2分别为优化前、优化后的所述双馈型风力发电机的转子转速，nw为所述风力机的转速；

将λ＝λopt代入式(9)，求得优化后的所述双馈型风力发电机的同步转速n1m＝λoptn1n；

5)根据

式中，n1为所述双馈型风力发电机得的同步转速，f1为所述双馈型风力发电机的定子额定频率，np为所述双馈型风力发电机的极对数；

将n1＝n1m＝λoptn1n代入式(10)，求得优化后所述双馈型风力发电机的定子额定频率f1n＝npλoptn1n/60。

本发明的有益效果是：随着齿轮箱增速比的降低，齿轮箱的体积减少，成本降低，故障率降低，从而整机系统的成本降低，系统运行的可靠性提升。

附图说明

图1为本发明采用的双馈型风力发电系统拓扑结构示意图。

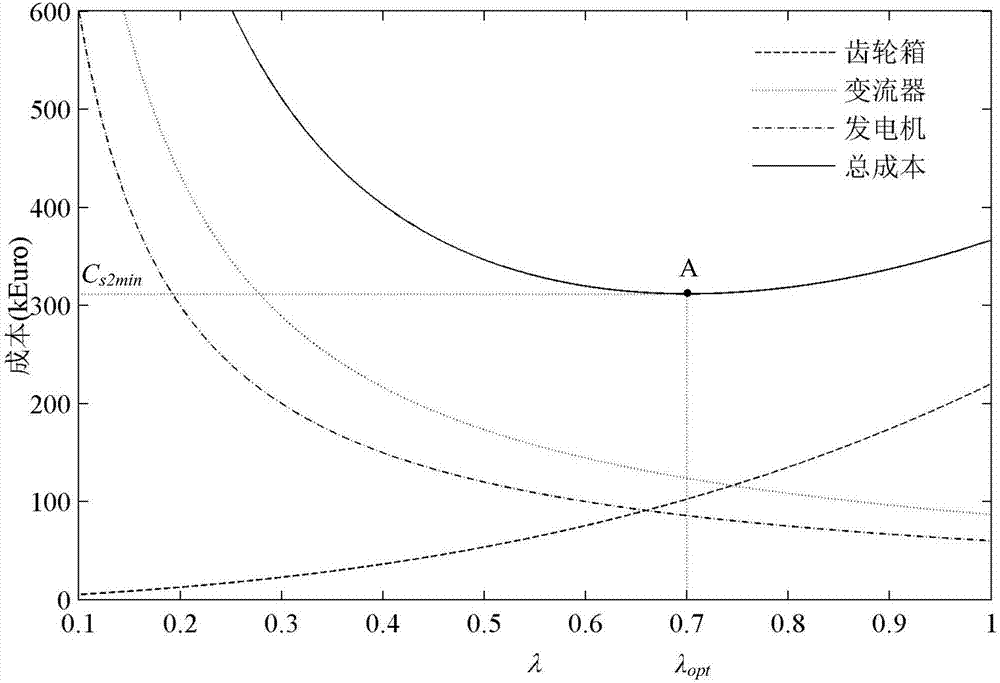
图2为优化后成本—齿轮箱增速比之比λ关系曲线图。

其中，1-风力机；2-齿轮箱；3-双馈型风力发电机；31-双馈型风力发电机的定子；32-双馈型风力发电机的转子；4-直流变流器；41-定子侧变流器；42-转子侧变流器；5-直流母线

具体实施方式

下面结合附图，对本发明作进一步详细说明。

如图1所示，本发明采用的双馈型风力发电系统包括风力机1、齿轮箱2、双馈型风力发电机3、直流变流器4、直流母线5；直流变流器4包括定子侧变流器41和转子侧变流器42；齿轮箱2、双馈型风力发电机3和直流变流器4统称为双馈型风电机组。齿轮箱2一端与风力机1连接，另一端与双馈型风力发电机转子32连接；定子侧变流器41一端与双馈型风力发电机定子31连接，另一端分别与转子侧变流器42、直流母线5连接；转子侧变流器42的另一端与双馈型风力发电机转子32连接。

本发明基于直流输电的低增速比双馈型风电机组优化设计方法，采用一种双馈型风力发电系统拓扑结构对双馈型风电机组进行优化设计及控制，具体包括以下步骤：

步骤1，假设优化前后风力机1的功率不变，双馈型风力发电机(dfig)3的极对数np及其定子31的感抗ls、转子32的感抗lr和定转子之间的互感lm保持不变，定子31的磁通ψs保持不变，令：

λ＝m/n(1)

式中，n、m分别为优化前、优化后齿轮箱2的变速比，且m<n，λ为优化后齿轮箱2的增速比与优化前齿轮箱2的增速比之比。

采用定子磁通矢量定向控制策略，求优化前后双馈型风力发电机3的定子电流、转子电流、总电流和直流变流器4的总电流之比。具体过程如下：

根据定子磁通矢量定向控制策略，在定子磁通矢量定向坐标系中，令定子磁通矢量方向与坐标系的d轴一致，则有：

式中，ψs为定子磁通，ψsd、ψsq分别为ψs的d轴和q轴分量；isd、ird分别为定子电流和转子电流的d轴分量；isq、irq分别为定子电流和转子电流的q轴分量；β为定子自感ls与定转子互感lm的比值，即：β＝ls/lm；

由式(11)的第二个方程可得到：isq＝-irq/β，则双馈型风力发电机3的输出功率p、定子磁通ψs和电流有如下关系：

式中，ωm为转子转速。

在优化前后功率和定子磁通保持不变的情况下，由式(12)有：

式中，ωm1、ωm2分别为优化前、优化后的转子转速，isq1、irq1分别为优化前定子电流和转子电流的q轴分量，isq2、irq2分别为优化后定子电流和转子电流的q轴分量。

根据式(13)和式(9)、式(11)，可得优化前后定子31的q轴电流和转子32的q轴电流之比分别为：

双馈型风力发电机3的定子侧通常运行于单位功率因数模式，即定子31的无功电流为0，转子32为系统提供励磁电流，结合式(11)，有：

式中，isd1、ird1分别为优化前定子电流和转子电流的d轴分量，isd2、ird2分别为优化后定子电流和转子电流的d轴分量。

则根据式(14)、式(15)，可求得优化前后定子电流之比为：

式中，is1、is2分别为优化前后dfig定子电流。

根据式(13)、式(14)，可得优化前后转子电流之比为：

即：

式中，ir1、ir2分别为优化前后双馈型风力发电机3的转子电流，α为优化前额定的转子d轴励磁电流ird1与定子q轴有功电流isq1的比值，即：α＝ird1/isq1，双馈型风力发电机3一旦确定，α值保持恒定。

根据式(14)、式(15)，可得优化前后双馈型风力发电机3的总电流之比为：

即：

式中，it1、it2分别为优化前后双馈型风力发电机3的总电流。

根据式(14)、式(15)，可得优化前后直流变流器4的总电流之比为：

即：

式中，ic1、ic2分别为优化前后直流变流器4的总电流。

步骤2，建立优化后双馈型风电机组的总成本cs2的计算模型，具体过程如下：

设优化设计前，双馈型风力发电机3的成本为ct1，齿轮箱2的成本为cg1，直流变流器4的成本为cc1，双馈型风电机组的总成本为cs1，则有：

cs1＝ct1+cg1+cc1(16)

设优化设计后，双馈型风力发电机3的成本为ct2，齿轮箱2的成本为cg2，直流变流器4的成本为cc2，双馈型风电机组的总成本为cs2，则有

cs2＝ct2+cg2+cc2(17)

在功率p不变的情况下，齿轮箱4的成本cg2主要由其变速比和扭矩大小来决定，随着λ的减少，可以估算为

cg2＝cg1(k0+k1λ+k2λ²+k3λ³)(18)

式中，k0、k1、k2、k3分别为齿轮箱4的成本曲线的拟合系数，用于拟合随λ变化的齿轮箱成本曲线,使之和实际齿轮箱成本曲线重合。

在电压等级相同的情况下，双馈型风力发电机3和直流变流器4的成本与其电流等级有关系，因而优化后的双馈型风力发电机3的成本ct2可以估算为：

将式(4)代入式(19)，则有：

优化后的直流变流器4的成本cc2可以估算为：

将式(5)代入式(21)，则有：

将式(18)、式(20)、式(22)代入式(17)，可得变速比减少后双馈型风电机组的总成本cs2为：

步骤3，根据优化后所述双馈型风电机组的总成本cs2的计算模型式(6)，求双馈型风电机组的优化设计参数，具体包括以下步骤：

1)如图2所示，以λ为横坐标、成本为纵坐标，根据式(18)、式(20)、式(22)、式(6)分别绘制齿轮箱2的成本cg2-λ曲线、双馈型风力发电机3的成本ct2-λ曲线、直流变流器4的成本cc2-λ曲线、双馈型风电机组总成本cs2-λ曲线，求出cs2的最小值cs2min，即优化后双馈型风电机组的最优成本，与之对应的λ即为最优齿轮箱增速比之比λopt；

2)根据式(1)，求得优化后的齿轮箱2的增速比m＝λoptn；

3)将λ＝λopt分别代入式(2)、式(3)，获得优化后的双馈型风力发电机3的定子电流is2和转子电流ir2分别为：

4)根据优化后与优化前的同步转速之比：

式中，n1n、n1m分别为优化前、优化后双馈型风力发电机3的同步转速，ωm1、ωm2分别为优化前、优化后的转子转速，nw为风力机1的转速；

将λ＝λopt代入式(9)，求得优化后的双馈型风力发电机3的同步转速n1m＝λoptn1n；

5)根据

式中，n1为dfig同步转速，f1为定子额定频率，np为dfig的极对数；

将n1＝n1m＝λoptn1n代入式(10)，求得优化后dfig的定子额定频率f1n＝npλoptn1n/60。

下面用一个例子对本发明做进一步说明。

实施例：

以某公司生产的双馈型风电机组为例，其主要参数为：p＝3mw，vs＝1650v(定子电压)，is＝600a，ir＝608a，n1n＝1000rpm，np＝3，齿轮箱增速比n＝80，lm＝99mh，ls＝99.99mh；齿轮箱成本cg1＝22万欧元(euro)，dfig成本ct1＝6万欧元，变流器成本cc1＝8.67万欧元，三者总成本cs1＝36.67万欧元；k0＝0，k1＝0.2，k2＝0.35，k3＝0.45，β＝1.01，α＝0.0884。

首先，根据式(18)、式(20)、式(22)、式(6)分别绘制优化后的齿轮箱成本cg2-λ曲线、dfig成本ct2-λ曲线、直流变流器成本cc2-λ曲线、双馈型风电机组中上述三者总成本cs2-λ曲线，如图2所示。从图2中可以看出，齿轮箱的成本cg2随着λ的降低而逐渐降低；变流器和dfig的成本(cc2、ct2)随着λ的降低而逐渐提高；总成本cs2先随着λ的降低而逐渐降低，后随着λ的降低而逐渐提高，存在最小值。找出图中最小值a点，此点即为最优点，其对应的横坐标λ值即为最优齿轮箱增速比之比λopt＝0.7，其对应的纵坐标cs2值即为优化后双馈型风电机组的最优成本cs2min＝311keuro＝31.1万欧元，节省了5.57万欧元，成本降低了15.2％。

其次，将λopt＝0.7代入式(1)，可求得优化后齿轮箱的变速比m＝56，以此和功率等级选择齿轮箱。

第三，将λopt＝0.7分别代入式(7)、式(8)，获得优化后的定子电流is2和转子电流ir2分别为：is2＝857a，ir2＝867a。

第四，将λopt＝0.7代入式(9)，求得优化后dfig的同步转速n1m＝700rpm；

最后，将n1＝n1m＝700rpm代入式(10)，求得优化后dfig的定子额定频率f1n＝35hz。