一种基于性能要求的变刚度弹簧设计方法与流程

本发明提供一种基于性能要求的变刚度弹簧的设计方法，属于机械弹簧设计领域。

背景技术：

机械弹簧按照其特征曲线(载荷与变形的函数曲线)来分一般分为线性和非线性两类，线性弹簧的刚度在变形过程保持不变，结构简单，制造方便，非线性弹簧的刚度在变形过程中开始会保持不变，但随着载荷的增大刚度会逐渐变化，有利于消除或缓和共振，稳定性好，可以承受较大的载荷。

但是上述机械弹簧在实际工程中存在如下缺陷：1、弹簧特征曲线满足性能要求的变化范围较小，超过了此范围则无法实现相应的功能，应用场合有很大的局限性；2、弹簧的刚度为常数或者开始为常数随后逐渐变化，设计者不能根据性能要求找到相应的弹簧，例如要求弹簧的刚度在变形中满足一定的力-变形关系，从而实现系统地某一个特殊功能，这是上述弹簧无法满足的。

技术实现要素：

为克服目前机械弹簧在实际工程中存在的缺陷，本发明提出一种基于性能要求的变刚度弹簧的设计方法，该方法能够根据设计需求改变弹簧的特征曲线，使得特征曲线在大范围内与目标曲线重合。本发明对等螺旋角圆锥螺旋弹簧(螺旋角α为常数)进行分析，得出弹簧丝直径d＝ar^b(a>0,b≥0)时载荷与变形的计算式；根据计算过程编写该计算式的程序，探究弹簧参数对特征曲线的影响规律；根据性能要求将影响参数带入程序迭代得出最优解。

本发明的技术方案：

一种基于性能要求的变刚度弹簧设计方法，步骤如下：

1.d＝ar^b时等螺旋角圆锥弹簧载荷与变形的计算式

等螺旋角圆锥弹簧的变形过程为，在轴向力的作用下，弹簧线圈压缩变形，线圈之间没有相互重叠，在这一阶段特征曲线为直线，弹簧刚度为常数，当有线圈刚开始压并时，此时为转折点，当载荷逐渐增大，弹簧特征曲线呈现为渐增型，弹簧刚度逐渐增大。通过对d＝ar^b进行分析可得，当0≤b≤0.5时，转折点表现为最下端线圈达到最大变形，弹簧从最下端线圈开始逐渐压并直至最上端，得出弹簧的变形计算式为：

式中p表示轴向载荷，d1、d2表示端部线圈直径，n0表示有效线圈数，l0表示弹簧极限变形长度，g表示剪切模量，d表示弹簧丝直径，a、b表示弹簧丝直径的设计参数，dt表示临界直径,n1表示临界线圈数(计算式为)。

当b>0.5时，转折点表现为最上端线圈达到最大变形，弹簧从最上端线圈开始逐渐压并直至最下端，得出弹簧的变形计算式为：

弹簧完全压并时为平面所满足的条件为：

r(θ+2π)-r(θ)≥d(3)

式中θ为弹簧线圈的螺旋极角，r表示弹簧线圈的半径函数且

2.弹簧参数对弹簧特征曲线的影响

根据式(1)和式(2)编写计算程序。已知参数d1、d2，n0，g,a,b对弹簧变形均有影响，利用控制变量法，将各参数带入程序中进行计算，根据结果可知g,n0不改变弹簧刚度的变化趋势和特征曲线的凹凸性。

图1(a)为参数d1、d2对特征曲线的影响，随着的增加，线性阶段所占比例逐渐减小，线性度越差；图1(b)为参数a的影响，a值有效的提高了弹簧的承载力，但对线性阶段所占比例则没有影响，不改变弹簧特征曲线的凹凸性；图1(c)(d)为参数b的影响，当0≤b≤0.5时，随着b的增加，特征曲线趋近于一条直线，线性度(线阶段的变形与总变形的比值)增加，当b＝0.5时特征曲线为完全线性，当b>0.5时，随着b的增加，特曲线的线性度越差。

3.特征曲线与目标函数曲线的拟合

(1)已知基于性能要求的目标函数满足：

pm＝f(e)(4)

式中pm表示外载荷，e表示工程应变(相对变形)。

现在需要找到一个弹簧的特征曲线：

p＝g(e)(5)

在0≤e≤0.5的条件下，特征曲线与目标函数曲线的重合度到达最好，判断依据是坐标所有点误差的平均值达到最小：

式中w表示所有点误差的平均值，m表示取点的数目。

(2)对参数b进行优化，已知参数d1、d2，b都对特征曲线的线性度有影响，d1、d2属于弹簧的基本设计参数,在设计时会根据工程需求确定好弹簧的大小，因此弹簧下端部线圈d2的大小是确定的，在此基础上我们先假定d1是已知的，给d1一个具体的大小。

在d1、d2已知的条件下，需确定a的取值范围，上述探究参数对特这曲线的影响已经得出a并不影响特征曲线的线性度，但需满足式(3)中的条件，带入可得：

a∈(a,b)(7)

式中a,b分别为取值的上下限。

在此条件下，从b＝0开始逐渐取值，带入计算程序中，根据式(6)的判断方法得出此条件下b的最优解。

(3)对参数d1进行优化，(2)中已经得出在假定d1已知的条件下b的最优解，则保证此b值不变，d1从大于和小于假定值逐渐取值，带入计算程序中，根据式(6)的判断方法得出此条件下d1的最有解。

(4)重复(2)，(3)过程，迭代得出最优解，若式(6)计算值满足：

wn+1>wn<wn-1…(8)

式中n表示迭代的次数。

则迭代停止，即可得出b和d1的最优解。

本发明的有益效果：本发明提供了一种基于性能要求的变刚度弹簧的设计方法，一方面在应变大范围内使得特征曲线和目标曲线的重合情况较好；另一方面设计者可根据工程中的性能要求设计相应的弹簧。

附图说明

图1(a)为参数d2/d1对特征曲线的影响。

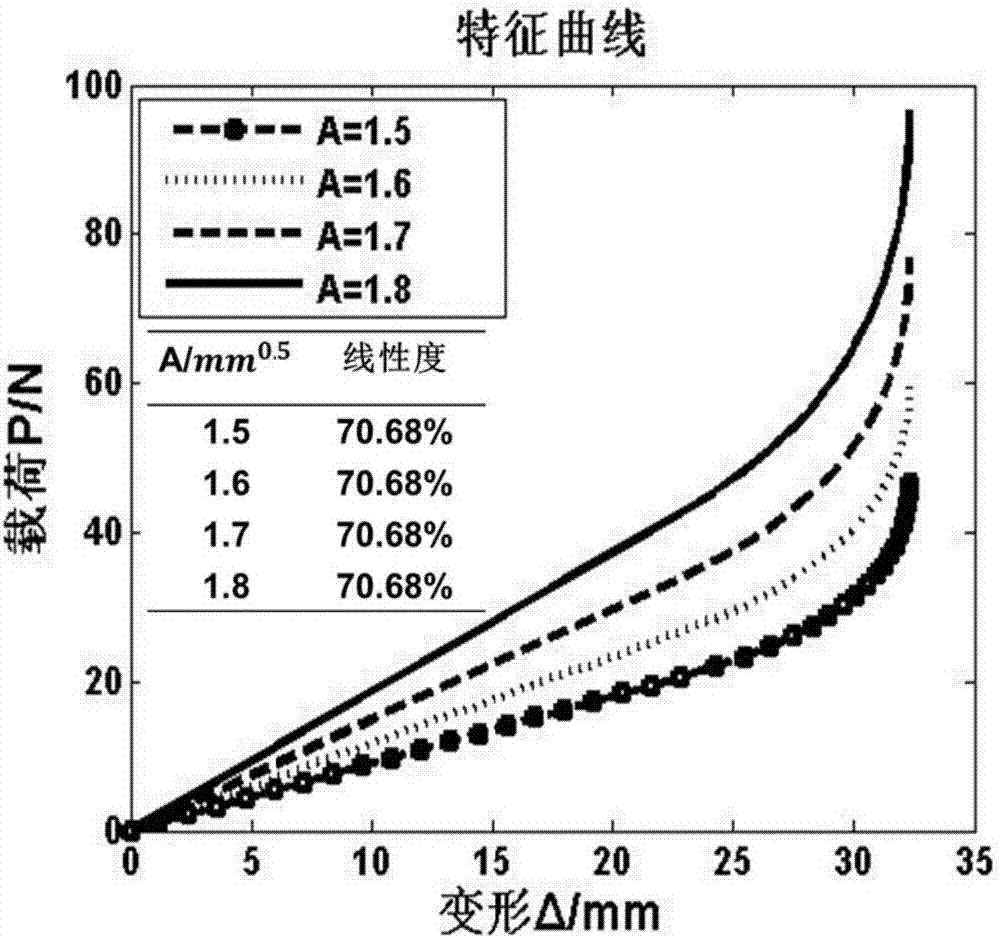
图1(b)为参数a对特征曲线的影响。

图1(c)为参数0≤b≤0.5时对特征曲线的影响。

图1(d)为参数b>0.5时对特征曲线的影响。

图2为d＝ar^b的弹簧设计示意图，以b＝1为例。

图3(a)为设计某微型压力传感器时，b的优化结果。

图3(b)为设计某微型压力传感器时，d1的优化结果。

图4为某微型压力传感器的设计示意图。

图中：①下端部线圈半径d2/2；②上端部线圈半径d1/2；③螺旋角α；④弹簧丝直径(满足d＝ar^b,以b＝1为例)；⑤端部线圈；⑥有效线圈n0；⑦极限变形长度l0；⑧弹簧总长度ls。

具体实施方式

以下结合附图和技术方案，进一步说明本发明的具体实施方式。

以设计某微型压力传感器为例：

(1)已知电容表面受到轴向载荷f作用，要想使得电容c与载荷f为线性关系，则需满足条件:ε为间隙中的介电常数，s为平板面积，h0为平板之间的初始距离，k为电容c与载荷f之间的直线斜率，可其调整大小。

(2)取剪切模量g＝81500mpa，螺旋角α＝5°，有效线圈数n0＝4,下端部线圈直径d2＝80mm，上端部线圈直径d1＝20mm，带入式(3)，得出a≤(0.414r^1-b)min，将其带入程序，根据图3(a)的结果可知b＝1.2时误差达到最小，弹簧特征曲线与目标曲线的重合情况较好。

(3)取b＝1.2，d1从小于和大于20mm分别取值，带入程序，根据图3(b)的结果可知d1＝17.5mm时误差达到最小，弹簧特征曲线与目标曲线的重合情况较好。

(4)将d1＝17.5mm带入(2)中，重复(2)过程，结合表1可知，误差仍

表1不同b值的平均误差

然在b＝1.2时达到最小，则迭代结束，因此b＝1.2,d1＝17.5mm时为最优解。

根据上述结果可知，利用本发明提供的基于性能要求的变刚度弹簧设计方法，某微型压力传感器的目标曲线和弹簧的特征曲线在应变0≤e≤0.5范围内有很好的重合度，所有点误差的平均值仅3.62％，克服了目前机械弹簧在工程中存在的缺陷。

以上仅为工程中的某一实例，设计者可根据实际性能需求对弹簧进行设计。