一种均匀截面梁结构的振动分析方法与流程

本发明属于结构动力学领域，具体涉及一种均匀截面梁结构的振动分析方法。

背景技术：

细长型结构广泛应用于船舶与海洋工程、建筑工程和航空航天等工程设备中，例如桥梁、杆系、轴系以及飞机机翼等。深入研究这类结构的振动特性及其参数影响规律在设备早期设计阶段振动噪声水平预估和实现低噪声设计具有重要的理论与实践指导意义。工程应用中常采用梁理论来处理这种细长型结构，以达到兼顾求解效率和计算精度的目的。

经典的梁理论主要有欧拉-伯努利和铁木申科两种理论，然而，欧拉-伯努利梁理论忽略了结构横向拉伸和剪切变形以及转动惯量的影响，仅适用于求解特定的细长梁结构；铁木申科梁理论虽然考虑了横向剪切变形和转动惯量的影响，但仍忽略了横向拉伸变形以及扭转时的翘曲变形，仅适用于短粗梁结构的横向弯曲问题。当梁结构的高跨比较大或者为薄壁结构时，这两种理论计算结果往往偏差较大甚至无法用于计算分析，此时必须采用新的三维梁理论。卡诺基于三维弹性理论提出了卡诺高阶截取拟合技术(相关文献为carrerae.aclassoftwo-dimensionaltheoriesforanisotropicmultilayeredplatesanalysis.[j].mem.accad.sci.torinocl.sci.fis.mat.natur,1995:49-87.carrerae.theoriesandfiniteelementsformultilayered,anisotropic,compositeplatesandshells[j].archivesofcomputationalmethodsinengineering,2002,9(2):87-140.)，并将该技术成功地引入到梁结构的研究中(相关文献为petrolom,zappinoe,carrerae.refinedfreevibrationanalysisofone-dimensionalstructureswithcompactandbridge-likecross-sections[j].thin-walledstructures,2012,56(2):49-61.)。该技术可以通过改变位移中未知变量的个数而衍生出很多的梁理论模型，而这只需对其核心部分稍加修改便可得到。基于卡诺高阶截取拟合技术，梁理论由低阶变成高阶会变得十分容易，这一系列的梁理论都可以通过同一个矩阵核心迭代而来，变化的只是迭代的次数。另一方面，该技术中位移里未知变量的个数可以根据问题的需求而确定，针对特定的工程梁问题，可以通过选择合适的未知变量的数量而达到相应的计算精度。如薄壁梁、弯曲、扭转、剪切局部载荷，各种静态和动态问题。

然而，已有的卡诺高阶截取拟合技术大部分是通过嵌入有限元方法来求解梁结构动力学问题，改变梁截面形状或增加单元数量往往需要重新建模分析，另外有限元方法普遍具有计算量大，计算精度不高，边界条件施加较为繁琐等缺点。因此，研究和建立一种能够适用多截面形状、多边界条件梁结构的振动分析方法具有十分重要的意义。

技术实现要素：

本发明的目的在于提供一种适用多边界条件、多截面形状梁结构的，且精度高、收敛快、计算成本低和计算方法简单的均匀截面梁结构的振动分析方法。

本发明的目的是这样实现的，包括以下步骤：

(1)提取梁结构的几何尺寸特性，将梁结构的位移场分离为截面面内位移和轴向位移，具体表达式为：

uk(x,y,z)＝φk(x,z)fk(y)

其中x和z为结构空间沿着梁截面方向的坐标，y为梁轴向坐标，uk(x,y,z)为梁结构的整体位移，k＝1，2，3分别表示x，y和z三个方向上的分量，φk(x,z)为截面面内位移，fk(y)为轴向位移。

(2)利用卡诺高阶截取技术对梁结构截面面内位移进行拟合，拟合形式如下：

其中，为二维泰勒展开的第τ项；ak0，ak1，ak2，…，akγ为相应泰勒展开项的系数；b1，b2，h1和h2为梁截面尺寸参数，n为二维泰勒展开的阶次，γ为二维泰勒展开的总项数。

(3)采用改进傅里叶级数对梁结构轴向位移进行延展，具体形式如下：

其中，m为改进傅里叶级数的截断项数，m＝-2,-1,...,m；bkm代表相应改进傅里叶展开项的系数，l为梁结构的总长度；

(4)结合梁结构截面面内位移和轴向位移，计算得到梁结构的整体位移，具体表达式如下：

其中，u1(x,y,z)，u2(x,y,z)和u3(x,y,z)分别对应空间坐标x，y和z三个方向上的位移分量，aτm，bτm和cτm为位移分量中相应项的系数。

(5)计算弹性板结构的应变向量和应力向量；

所涉及弹性板结构的应变向量的表达式为：

ε＝[εx,εy,εz,γxy,γyz,γxz]^t

其中，ε表示弹性板结构的应变向量；上标t表示转置；εx，εy和εz为正应变分量；γxy，γyz和γxz为切应变分量，且有

所涉及应力向量的表达式为：

σ＝dε

其中，σ表示弹性板结构的应力向量，d为结构材料系数矩阵。

(6)计算梁结构的应变能和动能方程，设置虚拟弹簧边界从而获取边界能，具体表达式如下：

其中，vs，tp和vp分别为梁结构的应变能、动能和边界能方程；t表示时间，ρ为材料的密度。kx0，ky0和kz0为梁结构y＝0端所设的虚拟弹簧边界的刚度系数，kxl，kyl和kzl为梁结构y＝l端所设的虚拟弹簧边界的刚度系数。

(7)建立结构拉格朗日能量泛函ω＝vs+vp-tp，然后对系数aτm，bτm和cτm求偏导并令其结果为零，即可得到梁结构的3×3阶核心质量矩阵和刚度矩阵。核心矩阵中的元素如下：

其中，k^mnij为核心刚度矩阵，m^mnij为核心质量矩阵；上角标i,j＝1,…,γ；m,n＝-2,-1,0,…,m；下角标a，b和c表示核心矩阵中元素的标号。和表示分别对x和z求一阶偏导，和表示分别对x和z求一阶偏导，ψm,y和ψn,y分别表示ψm和ψn对y求一阶导数。d11,…,d66为结构材料系数矩阵d中的元素。

(8)通过迭代循环核心矩阵求得整体的质量矩阵、刚度矩阵以及总体质量矩阵m，进而得到结构的特征方程；

所述质量矩阵和刚度矩阵的求解方法为：指针i，j由1取到n+1循环核心刚度矩阵kmnpqij得到子子矩阵kmnpq，指针p，q由1取到p+3循环子子矩阵kmnpq得到子矩阵kmn，指针m，n由1取到m+3循环子矩阵kmn得到总体刚度矩阵k；

所述结构的特征方程表达式为：

(k-ω²m)a＝0

其中ω为圆频率，a为对应ω的特征向量；

(9)求解梁结构的特征方程矩阵并计算得到固有频率和振型。

本发明的优势在于：本发明实现了对梁理论阶次和轴向拟合基函数截断级数的参数化分析，改变梁理论阶次或增加截断项数，只需简单地增加核心矩阵的循环迭代次数；本发明中梁截面位移函数以二维泰勒多项式进行拟合，并无特殊针对性，理论上该方法适用于任意截面形状的均匀梁结构；本发明中梁轴向位移函数以傅里叶级数进行全求解域拟合，与传统有限元方法相比，具有收敛速度快计算精度高等特点；本发明只需要通过控制边界弹簧的刚度来满足结构的不同边界条件要求，而不需要对程序做任何修改。总的来说本发明的方法具有适用任意边界条件和任意截面形状、精度高、收敛快、计算成本低等特点。

附图说明

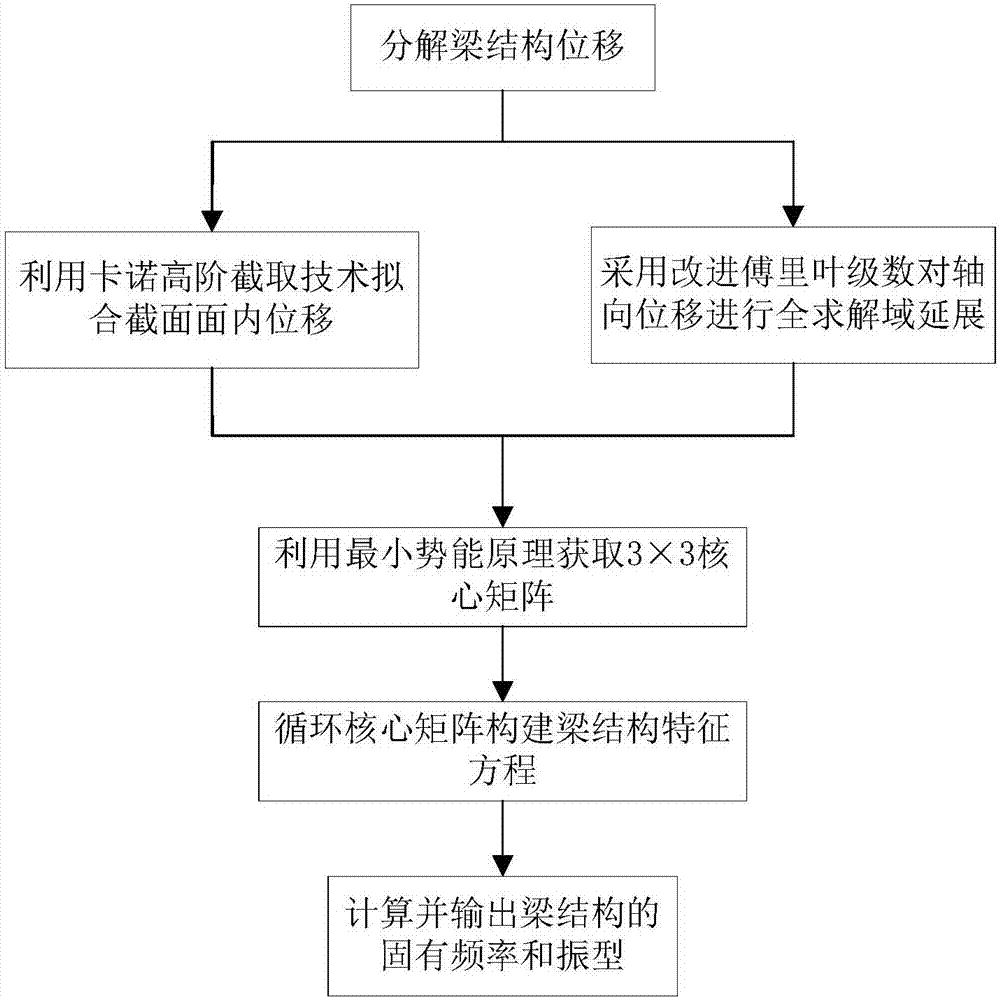
图1为本发明的流程图；

图2为方形空心梁结构示意图；

图3为刚度矩阵的装配示意图。

具体实施方式

为使本发明解决的技术问题、采用的技术方案和达到的技术效果更加清楚，下面结合附图对本发明做进一步描述。本发明方法的执行步骤如图1所示。

考虑一个方形空心截面梁结构，如图2所示，截面尺寸b1＝h1＝0，b2＝h2＝0.2m，梁材料为各向同性，杨氏模量e＝75gpa，密度ρ＝7800kg/m³，泊松比μ＝0.3。梁的长度l为2m或20m。对应的高跨比h2/l分别为0.1和0.01，分别代表着短粗梁和细长梁结构。梁两端简支无外加载荷。利用本发明方法对其进行求解，二维泰勒展开阶次n＝2。具体步骤如下：

(1)提取空心截面梁的几何尺寸，建立空间直角坐标系，根据梁结构长度方向尺寸远大于另外两个方向这一特性，将梁结构的位移场分离为截面面内位移和轴向位移，具体表达式为：

uk(x,y,z)＝φk(x,z)fk(y)

其中x和z为结构空间沿着梁截面方向的坐标，y为梁轴向坐标，uk(x,y,z)为梁结构的整体位移，k＝1，2，3分别表示x，y和z三个方向上的分量，φk(x,z)为截面面内位移，fk(y)为轴向位移。

(2)利用卡诺高阶截取技术对梁结构截面面内位移进行拟合，由于该梁结构截面较为复杂，故选取二维泰勒展开阶次n＝2进行计算，泰勒展开式项数γ＝(n+1)(n+2)/2＝6，具体拟合形式如下：

其中，为二维泰勒展开的第τ项，ak0,ak1,ak2,…,akγ为相应泰勒展开项的系数，akτ为二维泰勒展开第τ项的系数，b1,b2,h1和h2为梁截面尺寸参数，n为二维泰勒展开的阶次，γ为二维泰勒展开的总项数。

(3)采用改进傅里叶级数对梁结构轴向位移进行延展，初步选取截断项数m＝10，具体形式如下：

其中bkm代表相应改进傅里叶展开项的系数，l为梁结构的总长度，两个sine项(m＝-2和m＝-1)，的引入是为了消除结构位移展开成传统傅里叶cosine级数时其本身及一阶导数在两端的不连续性，从而加快方法的收敛速度。

(4)结合梁结构截面面内位移和轴向位移，并将系数进行整合，即可得到梁结构的整体位移，具体表达式如下：

其中，u1(x,y,z)，u2(x,y,z)和u3(x,y,z)分别对应空间坐标x，y和z三个方向上的位移分量，aτm，bτm和cτm为梁结构的整体位移中相应项的系数。

(5)计算梁结构的应变向量和应力向量，振动应变具体形式如下：

ε＝[εx,εy,εz,γxy,γyz,γxz]^t

其中，εx，εy和εz为正应变分量，γxy，γyz和γxz为切应变分量；ε表示梁结构的应变向量，t表示转置。梁材料为各向同性，杨氏模量e＝75gpa，泊松比μ＝0.3，通过弹性力学中的物理方程计算振动应力具体形式如下：

σ＝dε

其中，σ表示梁结构的应力向量，d为结构材料系数矩阵。

(6)利用梁结构的应变向量和应力向量计算梁结构的应变能和动能，同时，对于两端简支边界，设置虚拟弹簧刚度以获取边界能：kx0＝10¹⁰，ky0＝0，kz0＝10¹⁰；kxl＝10¹⁰，kyl＝0，kzl＝10¹⁰。具体表达式如下：

其中，vs，tp和vp分别为梁结构的应变能，动能和边界能方程。t表示时间，ρ为材料的密度。kx0，ky0和kz0为梁结构y＝0端所设的虚拟弹簧边界的刚度系数，kxl，kyl和kzl为梁结构y＝l端所设的虚拟弹簧边界的刚度系数。

(7)建立结构拉格朗日能量泛函ω＝vs+vp-tp，然后对其中的系数aτm，bτm和cτm求偏导并令其结果为零，即可得到梁结构的3×3阶核心质量矩阵和刚度矩阵。

求得核心矩阵中的元素如下：

其中k^mnij为核心刚度矩阵，m^mnij为核心质量矩阵；上角标i,j＝1,…,γ；m,n＝-2,-1,0,…,m；下角标a，b和c用以表示核心矩阵中的各个元素，例如ab表示矩阵中第a行第b列的元素。和表示分别对x和z求一阶偏导，和表示分别对x和z求一阶偏导，同理ψm,y和ψn,y分别表示ψm和ψn对y求一阶导数。d11,…,d66为结构材料系数矩阵d中的元素。

(8)如图3所示，通过迭代循环核心矩阵求得整体的质量矩阵和刚度矩阵：指针i，j由1取到γ＝6循环核心矩阵k^mnij得到子矩阵k^mn，指针m，n由-2取到m＝10循环子矩阵k^mn得到总体刚度矩阵k。通过相同的方法循环核心质量矩阵m^mnij得到总体质量矩阵m，进而得到结构的特征方程：

(k-ω²m)a＝0

其中ω为固有频率，a为对应ω的特征向量。

(9)应用arnoldi算法建立matlab求解器求解梁结构的特征方程矩阵输出其固有频率和振型。并进行收敛性判断：给予初始的改进傅里叶截断项数m1，算得结果并进行存储，增加截断项数至m2，通过前后两次结果的对比，判断计算结果是否收敛。

计算结果如表1所示，表1中给出了不同截断项数m下本方法计算出的结构整体的前五阶弯曲频率。细长梁指高跨比h2/l为0.01，短粗梁指高跨比h2/l为0.1，以传统的卡诺高阶梁理论计算结果作为参考。从表中可以看出，本发明方法无论是在处理细长梁还是短粗梁均具有较好的收敛速度，当截断项数为10时，前五阶弯曲模态已基本收敛。另一方面，通过与参考值对比可以发现本研究方法具有很好的计算精度。

表1梁结构前五阶弯曲模态收敛性分析(hz)

注：参考值源自论文carrerae,petrolom,nalip.unifiedformulationappliedtofreevibrationsfiniteelementanalysisofbeamswitharbitrarysection[j].shock&vibration,2015,18(3):485–502.