一种城市中SO2浓度值的预测方法与流程

本发明涉及气体含量检测技术领域，尤其涉及一种城市中SO2浓度值的预测方法。

背景技术：

伴随着人口高速增长所带来的自然资源过渡消耗和破坏，如气候改变、滥伐森林，尤其是环境污染。当前，有超过半数的人群生活在城市中，并且到2050年这个比例有望达到66％。据最新的城市空气质量报告可知，在中低收入国家的98％的10万人口级别及以上城市的居民不能满足世界卫生组织标准。

空气质量的定量预测从方法上主要有数值预测和统计预测。其中，数值预测方法较多的依赖于高分辨率的气象初始场和详尽的排放源清单数据，鉴于目前我国环境信息化现状，此方法尚不成熟。而统计预测方法的预测精度并不令人满意。但随着新技术和新理论的发展，人工智能和神经网络在空气质量预测方面发挥了较好的作用，因其过拟合、隐层节点难以确定和寻找结构参数复杂等缺点，导致训练速度和效率下降。

支持向量机(Support Vector Machine，SVM)是Corinna Cortes和Vapnik等于1995年首先提出的，它在解决小样本、非线性及高维模式识别中表现出许多特有的优势，并能够推广应用到函数拟合等其他机器学习问题中。在机器学习中，支持向量机(SVM，还支持矢量网络)是与相关的学习算法有关的监督学习模型，可以分析数据，识别模式，用于分类和回归分析。

支持向量机作为一种新的数据挖掘技术，在处理回归、分类和时间序列预测等方面得到了成功应用，如李龙等提出了一种基于支持向量机和特征向量的PM2.5浓度预测模型；陈柳提出了一种支持向量机和小波分析的SO2浓度预测模型。

支持向量机虽然取得较好发展，然而它仍有不足之处。支持向量机的本质是求解数学上的凸二次规划问题，而在大气污染环境当中，“内因是排放，外因是气象”已达成普遍认知，在外因中，风向、风速、气压和相对湿度等因素对大气污染的影响存在不同程度上，如把影响大气污染物浓度的因素均考虑在模型内，势必会加重训练负担，从而降低训练精度。如何克服不足，提高支持向量机的训练速度，推广其在预测空气质量参数效果，将会显得尤为重要。

技术实现要素：

本发明的目的在于提供一种城市中SO2浓度值的预测方法，从而解决现有技术中存在的前述问题。

为了实现上述目的，本发明采用的技术方案如下：

一种城市中SO2浓度值的预测方法，包括如下步骤：

S1，建立气象数值模型，并利用所述气象数值模型生成目标区域的气象场数据；同时，收集所述目标区域的SO2浓度的历史数据；

S2，利用如下公式，对所述气象场数据和所述SO2浓度的历史数据分别进行归一化处理，得到各因子的初始预测因子集：

式中，x、xn分别为归一化前和归一化后的浓度序列值；xmin、xmax分别为原序列x的最大值和最小值；

S3，将所述气象场数据和所述各因子的初始预测因子集分别利用偏最小二乘回归法提取主成分，筛选出最优预测因子集；

S4，将所述最优预测因子集输入到最小二乘支持向量机模型中进行训练，得到优化的最小二乘支持向量机模型；

S5，利用优化的最小二乘支持向量机模型，对预测样本进行预测，得到SO2浓度的预测值。

优选地，S1中，所述气象数值模型采用WRF。

优选地，S4包括如下步骤：

S401，根据训练样本在最小二乘支持向量机模型中，将目标函数描述为：

式中，xi为第i个样本输入向量，yi为第i个样本输出向量，l为样本容量，为非线性问题核函数，ω为权矢量，b为偏差值，T为转置符号，θi为第i个估计值和实测值之间的误差变量，γ为惩罚系数；

S402，引入拉格朗日函数对目标函数进行优化，得到下式：

式中，为目标函数求解值，αi为拉格朗日乘子；

S403，对S402得到的函数计算偏导数，得到下式：

S404，根据S403的偏导数，得到如下线性方程组：

其中，q为单位矩阵；为核函数矩阵；a为拉格朗日乘子集；b为偏差值；

S405，根据Mercer条件，由于核函数表示为：

故

将该核函数带入到线性方程组中，根据最小二乘法求解a和b；

S406，将S405求解得到的核函数带入KKT最优条件，得到如下的用于预测的优化后的最小二乘支持向量机模型：

式中，δ为核函数宽度。

本发明的有益效果是：本发明实施例提供的城市中SO2浓度值的预测方法，通过结合气象数值模型，弥补了气象场数据不足的问题；通过采用偏最小二乘回归法有效的解决了自变量系统中的变异信息，同时又对因变量给予了解释，克服了变量间的共线性问题，减少了计算量；另外，在基于径向基核函数的最小二乘支持向量机模型中，通过确定惩罚系数和核函数，极大的减少了利用最小二乘支持向量机模型进行预测计算的复杂性。

附图说明

图1是本发明实施例提供的城市中SO2浓度值的预测方法的流程示意图；

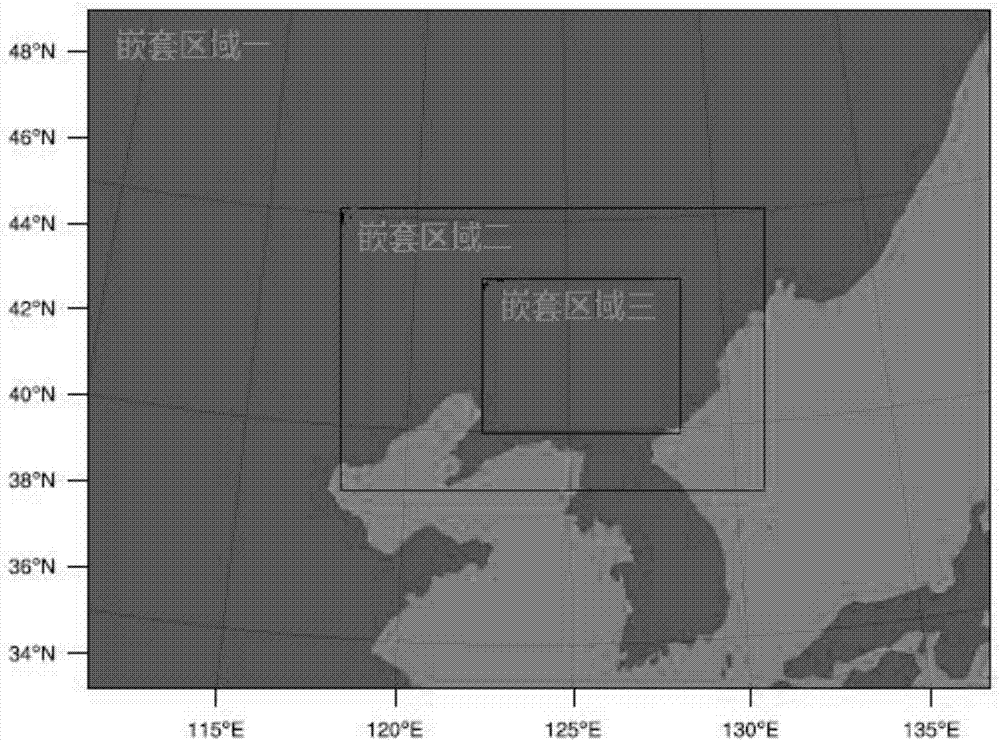
图2是本发明实施例中确定的气象数值模型的范围示意图；

图3是本发明实施例中SO2浓度值的相关分析示意图。

具体实施方式

为了使本发明的目的、技术方案及优点更加清楚明白，以下结合附图，对本发明进行进一步详细说明。应当理解，此处所描述的具体实施方式仅仅用以解释本发明，并不用于限定本发明。

如图1所示，本发明实施例提供了一种城市中SO2浓度值的预测方法，包括如下步骤：

S1，建立气象数值模型，并利用所述气象数值模型生成目标区域的气象场数据；同时，收集所述目标区域的SO2浓度的历史数据；

S2，利用如下公式，对所述气象场数据和所述SO2浓度的历史数据分别进行归一化处理，得到各因子的初始预测因子集：

式中，x、xn分别为归一化前和归一化后的浓度序列值；xmin、xmax分别为原序列x的最大值和最小值；

S3，将所述气象场数据和所述各因子的初始预测因子集分别利用偏最小二乘回归法提取主成分，筛选出最优预测因子集；

S4，将所述最优预测因子集输入到最小二乘支持向量机模型中进行训练，得到优化的最小二乘支持向量机模型；

S5，利用优化的最小二乘支持向量机模型，对预测样本进行预测，得到SO2浓度的预测值。

上述方法中，利用气象数值模型生成目标区域的气象数据，从而弥补了现有技术中气象场数据不足的问题，气象数据的丰富和完整，可以使得预测得到的SO2浓度数值更加准确。

同时，上述方法中，采用了偏最小二乘回归法，有效的概解决了自变量系统中的变异信息，同时又对因变量给予了解释，克服了变量间的共线性问题，减少了计算量。

另外，在本发明中，采用了最小二乘支持向量机模型，由于支持向量机模型为基于统计学习理论和结构风险最小化思想的模型，具有独立的理论背景和分类思想，所以，使得本发明实施例提供的方法具有独立的理论背景和分类思想。另外，在基于径向基核函数的最小二乘支持向量机模型中，通过确定惩罚系数和核函数，极大的减少了利用最小二乘支持向量机模型进行预测计算的复杂性。

本发明实施例中，S1中，所述气象数值模型可以采用WRF。

WRF(Weather Research and Forecast Model)主要面向对象是天气预报和天气研究。WRF中有NMM和ARW两种框架可以选择，可以作为全球模式进行天气预报，也可以作为区域模式进行天气现象的数值模拟。WRF是非静力平衡的数值模式，垂直方向采用eta坐标。

如本领域技术人员可以理解的，气象数值模型还可以使用ARPS、RegCM和CESM。

其中，ARPS(Advanced Regional Prediction System)针对中小尺度天气研究开发的数值模式，垂直方向采用高度坐标。

RegCM(Regional Climate Model)是基于MM5发展起来的静力平衡区域气候模式，主要面向区域气候模拟，计算相对稳定。

CESM(Community Earth System Model)是地球系统模式，里面的大气分量CAM(Community Atmospheric Model)也是一种常用的非静力平衡大气模式，主要面向气候方面的研究。CAM垂直方向采用混合坐标。

ARPS、RegCM和CESM三种模式是针对某一类型的问题细化的。RegCM的设计主要是面向区域气候领域，计算稳定，静力平衡，整体计算规模会比WRF小一些。CESM(CAM)只支持全球模拟，也是面向气候，环流等等研究，垂直方向上混合坐标，对于很多有强垂直运动的天气现象并不合适。ARPS则是对天气研究进行了强化，垂直方向高度坐标能够更好地解析垂直速度，但是模式也很不稳定。

而WRF模式，非静力平衡，垂直方向采用eta坐标，能够满足大部分中尺度的天气研究。最近几年WRF也开始作为区域气候模式使用，一定程度上也是因为eta坐标的特点和里面包含大量的物理参数化方案(WRF的扩展性是这些模式中最好的)。WRF在全球模式下可以进行天气预报。WRF还包含理想模型，从单柱模式到理想飑线到理想台风，WRF的理想模式可以用于理论研究。WRF甚至还包含单独的大气化学模块，可以进行气溶胶的预报等等。WRF还有一个同化系统WRFDA，里面有三维变分，四维变分，集合卡尔曼滤波等等。所以，本实施例中，采用WRF模型具有更好的代表性。

在本发明的一个优选实施例中，S4可以包括如下步骤：

S401，根据训练样本在最小二乘支持向量机模型中，将目标函数描述为：

式中，xi为第i个样本输入向量，yi为第i个样本输出向量，l为样本容量，为非线性问题核函数，ω为权矢量，b为偏差值，T为转置符号，为第i个估计值和实测值之间的误差变量，γ为惩罚系数；

S402，引入拉格朗日函数对目标函数进行优化，得到下式：

式中，为目标函数求解值，αi为拉格朗日乘子；

S403，对S402得到的函数计算偏导数，得到下式：

S404，根据S403的偏导数，得到如下线性方程组：

其中，q为单位矩阵；为核函数矩阵；a为拉格朗日乘子集；b为偏差值；

S405，根据Mercer条件，由于核函数表示为：

故

将该核函数带入到线性方程组中，根据最小二乘法求解a和核函数；

S406，将S405求解得到的核函数带入KKT最优条件，得到如下的用于预测的优化后的最小二乘支持向量机模型：

式中，δ为核函数宽度。

其中，KKT(Karush-Kuhn-Tucker)最优化条件(是Karush[1939]以及Kuhn和Tucker[1951]先后独立发表出来的。这组最优化条件在Kuhn和Tucker发表之后才逐渐受到重视，因此许多书只记载成Kuhn-Tucker最优化条件)是指在满足一些有规则的条件下,一个非线性规划(Nonlinear Programming)问题能有最优化解的一个必要和充分条件。

Mercer(人名)条件可以表述为任何半正定的函数都可以作为核函数。所谓半正定的函数f(xi,xj)，是指拥有训练数据集合(x1,x2,...xn)，定义一个矩阵的元素aij＝f(xi,xj)，这个矩阵为n*n的，如果这个矩阵是半正定的，那么f(xi,xj)就称为半正定的函数。Mercer条件不是核函数的必要条件，只是一个充分条件，即还有不满足Mercer条件的函数也可以是核函数。

具体实施例：

本发明的具体实施例，利用上述本发明实施例提供的城市中SO2浓度值的预测方法，进行SO2浓度的预测。

其中，气象数值模型的范围确定结果如图2所示，图中，横坐标是经度值，向右为正，纵坐标是纬度值，向北为正。该图中，通过三重嵌套，逐步提高气象场的分辨率，如第一重嵌套的空气分辨率为36km×36km，第二重嵌套可提高到12km×12km，第三重嵌套则已提高到4km×4km。由此可见，气象场数据的分辨率越来越精细，提供的数据越来越丰富。

利用优化的最小二乘支持向量机模型进行SO2浓度的预测后，对得到的结果进行相关性分析，其结果如图3所示，在图3中，横坐标是监测的SO2实际值，纵坐标是通过本发明实施例提供的方法预测得到的SO2浓度值。经相关性分析，从图中可见，相关性可达0.88。

可见，针对指定区域的SO2浓度预测，采用本发明实施例提供的方法可以得到更加精确的预测浓度值。

通过采用本发明公开的上述技术方案，得到了如下有益的效果：本发明实施例提供的城市中SO2浓度值的预测方法，通过结合气象数值模型，弥补了气象场数据不足的问题；通过采用偏最小二乘回归法有效的概解决了自变量系统中的变异信息，同时又对因变量给予了解释，克服了变量间的共线性问题，减少了计算量；另外，在基于径向基核函数的最小二乘支持向量机模型中，通过确定惩罚系数和核函数，极大的减少了利用最小二乘支持向量机模型进行预测计算的复杂性。

以上所述仅是本发明的优选实施方式，应当指出，对于本技术领域的普通技术人员来说，在不脱离本发明原理的前提下，还可以做出若干改进和润饰，这些改进和润饰也应视本发明的保护范围。