一种动中通天线系统辨识方法与流程

本发明涉及动中通天线伺服控制系统辨识技术领域，特别是指一种动中通天线系统辨识方法。

背景技术

动中通天线伺服控制系统主要包括电机、驱动器、减速机、齿轮传动、天线面及馈源网络，由于负载转动惯量、传动链阻尼、齿隙等无法准确获取，根据伺服系统工作原理直接建模得到准确的数学模型非常困难，因此现有技术中通常采用系统辨识方法进行建模。

目前，动中通天线系统辨识过程分为生成辨识信号、编写程序、采集数据、选择模型形式、参数拟合、模型误差对比、模型修正等过程，反复迭代，直到模型误差满足要求。

采用上述方式的辨识过程存在如下不足：

1)辨识过程不连续，信号生成、数据采集、数据处理在多个软件平台之间切换，工作量大。

2)模型形式、模型阶次需要预设，系统辨识主要辨识的是预设传递函数的参数，无法体现模型其他信息。

3)根据辨识误差，反复修正模型阶次，直到误差满足要求，工作效率不高。

4)仅适用于较低阶次模型的系统辨识，模型阶次较高时辨识误差较大。

技术实现要素：

有鉴于此，本发明的目的在于避免上述背景技术中的不足之处而提供的一种动中通天线系统辨识方法，其具有使用操作方便，辨识模型阶次准确、辨识精度高的特点。

为了实现上述目的，本发明所要解决的技术问题是由以下技术方案实现的：

一种动中通天线系统辨识方法，该方法用于获得由状态空间描述的动中通天线的数学模型，包括以下步骤：

(1)给定辨识激励信号；具体方式为，

生成伪随机序列，将伪随机序列作为半实物仿真平台的辨识输入；根据电机减速比和齿轮传动比，计算电机驱动器速度，将电机驱动器速度作为给定速度通过can总线发送到天线的电机驱动器，控制天线电机按照该给定速度转动；

(2)辨识数据采集；具体方式为，

采集并记录天线的给定速度、方位角度和俯仰角度；

(3)数据预处理；具体方式为，

从辨识采集的数据中剔除野值，根据辨识输入输出矩阵定义，将预处理后的输入输出数据代入到矩阵中，得到辨识输入矩阵u和输出矩阵y；

(4)确定模型阶次；具体方式为，

根据状态空间离散状态方程的伪随机序列响应关系y＝hu，通过矩阵运算求解hankel矩阵h；选择期望的模型最大阶次，构建子矩阵h1，对子矩阵h1进行奇异值分解：

h1＝vγ²u^t，

γ为对角矩阵，其对角元素是h1的奇异值，v、u为正交矩阵；

根据奇异值的大小确定辨识模型阶次k；

(5)确定状态方程矩阵；具体方式为，

选择矩阵v的前k行、矩阵u的前k列，矩阵γ的k行k列，构构建新的矩阵v、u、γ，得到能观矩阵p、能控矩阵q：

p＝vγ,q＝γu^t，

选择矩阵h的2～k+1行、2～k+1列，构建子矩阵h2，得到状态方程矩阵a、b、c，其中，a＝p^-1h2q^-1，b为矩阵q的第一列，c为矩阵p的第一行；

(6)对动中通天线进行建模，天线的状态空间表示如下：

xi+1＝axi+bui

yi＝cxi

其中，xi为状态变量，yi为输出变量；

完成动中通天线系统辨识建模。

可选的，所述伪随机序列由matlab软件生成，所述伪随机序列的参数设置为：时钟周期0.01秒，信号长度2047，重复周期4，信号幅度2°/s。

可选的，所述步骤(4)和步骤(5)中奇异值分解的方式为采用matlab软件中的svd函数进行分解。

本发明与背景技术相比具有如下优点：

1)本发明利用半实物仿真平台进行天线系统辨识，可以结合matlab和半实物仿真平台的接口，便于利用matlab强大的数学功能，具有编程简单、操作使用方便的优点。

2)本发明通过输入输出数据构建hankel矩阵，通过矩阵分解得到的奇异值从而判定模型阶次，不需要反复试凑确定模型阶次。

3)本发明采用半实物仿真平台构成高速can总线数据采集系统，实时性高，保证了数据的准确性。

附图说明

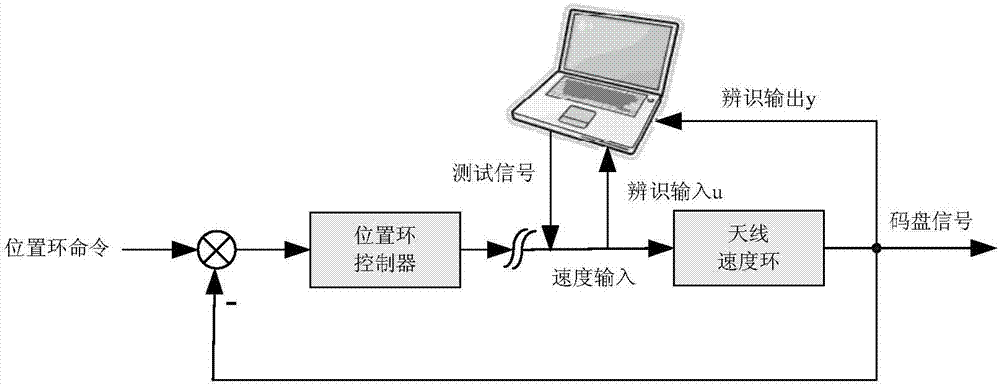
图1是本发明实施例中动中通天线系统辨识平台的结构框图；

图2是本发明实施例中动中通天线系统辨识过程的流程图。

具体实施方式

一种动中通天线系统辨识方法，该方法用于获得由状态空间表示的天线的数学模型。状态空间描述包括状态方程和输出方程，状态方程是描述系统状态变量和输入变量之间关系的一阶向量微分方程或差分方程，输出方程是描述系统输出变量与系统状态变量和输入变量之间函数关系的代数方程。状态空间表示如下：

xi+1＝axi+bui

yi＝cxi，

其中，矩阵a为系统矩阵或状态矩阵，b为控制矩阵或输入矩阵，矩阵c为输出矩阵或者观测矩阵。该辨识方法的主要任务就是完成对矩阵a、b、c的求解。

该方法包括以下步骤：

①给定辨识激励信号；具体方式为，

选取伪随机信号作为辨识输入，伪随机信号由matlab生成；根据减速机减速比和齿轮传动比，计算电机转速，通过can总线发送到电机驱动器，控制天线按照该期望速度转动；

②辨识数据采集；具体方式为，

采集并记录天线的给定速度、方位角度和俯仰角度；

③数据预处理；具体方式为，

从辨识采集的数据中剔除野值，根据辨识输入输出矩阵定义，计算输入矩阵、输出矩阵内部元素数值，构建辨识的输入矩阵u和输出矩阵y；

④确定模型阶次；具体方式为，

离散状态方程零初始状态下的脉冲响应可以表示成y＝hu，利用步骤③中的输入矩阵u和输出矩阵y，通过矩阵运算求解hankel矩阵h；接着，选择期望的模型最大阶次，可选的期望模型阶次不超过40，构建子矩阵，并对子矩阵进行奇异值分解，根据奇异值大小确定辨识模型阶次；

⑤确定状态方程模型；具体方式为，

状态方程为平衡实现形式，根据模型阶次构建新的hankel矩阵，进行奇异值分解，得到能观矩阵p、能控矩阵q，根据平衡实现和hankel矩阵关系，求解矩阵a、b、c，完成动中通天线系统辨识建模。

具体来说，如图1和2所示，一种动中通天线系统辨识方法，其针对的动中通天线可以为ae座架、aec座架或者ace座架天线，各轴系相互正交，耦合度低，辨识过程可以只考虑单个轴系，将天线系统作为单输入单输出(siso)系统。

该方法采用半实物仿真机and5436、matlab软件及simulink工具搭建系统辨识平台，其中，由matlab软件编制伪随机序列信号生成、数据处理、辨识算法等，simulink工具搭建天线运动控制及数据采集模块，全部软件在and5436仿真机内运行。

and5436仿真机运行程序，完成辨识数据采集后，由matlab进行数据处理，构造输入、输出矩阵。下一步需要确定模型阶次，具体方式为：根据离散状态方程伪随机序列信号响应，由输入矩阵和输出矩阵解算hankel矩阵h，进一步构造新的hankel矩阵h1，对矩阵h1进行奇异值分解，确定重要奇异值数量，从而确定模型阶次。最后，根据模型阶次，构建新的奇异值分解子矩阵，根据平衡实现和hankel矩阵关系，解算状态方程中的待定矩阵a、b、c，从而最终确认待辨识天线的状态方程。

具体步骤如下：

①给定激励信号

系统辨识时，首先给定天线激励信号，天线按照给定速度转动。本例选取伪随机序列信号作为辨识输入，伪随机序列具有良好的随机性且其自相关性和功率谱是对白噪声的近似，能够很好地削减测量噪声对辨识的影响，是用于辨识的理想激励。伪随机信号参数有时钟周期，信号长度，重复周期数以及信号幅度等。

动中通天线口径一般在0.3米～1.2米之间，谐振频率在10hz～45hz之间，根据动中通天线的结构和伺服系统特性，伪随机序列信号的参数选择为时钟周期0.01s，信号长度2047，重复周期4，信号幅度2°/s。

matlab编写伪随机序列程序，生成的伪随机序列信号作为天线的速度指令，利用半实物仿真平台and5436和simulink接口模块搭建can通信模块，通过can总线发送给天线驱动器，控制天线按照给定速度转动。

②辨识数据采集

辨识输入为伪随机序列信号，通过can总线发送给电机驱动器，辨识输出是码盘输出的轴角数据，通过can总线上报，辨识过程中定时采集并记录can总线上轴角编码数据和天线给定速度数据，采集记录的时间间隔为10ms，为了保证数据输入输出的对应性和一致性，将辨识过程中，每组辨识数据中包含天线给定速度和轴角。利用半实物仿真平台and5436和simulink接口模块搭建can通信模块和数据保存模块。

③数据预处理

辨识输入的伪随机序列的前500个点给定速度为0，计算前500个采样点的轴角平均值作为角度初始值，剔除异常角度值，得到辨识输入输出预处理数据。

将第i次速度给定值(即输入数据)表示为ui，第i次角度采集值(即输出数据)表示为yi，则输入矩阵为

输出矩阵为

y＝[y0y1y2...yp]，

上述两式中，q表示采样总数，p表示单周期伪随机序列长度，矩阵u为p行q列。

通过matlab编写m文件，实现数据的自动导入，并将数据按照输入输出矩阵形式存储。

④确定模型阶次

根据输入输出矩阵，计算hankel矩阵h，矩阵h计算公式为：

h＝yu^t(uu^t)^-1，

式中，u表示输入矩阵，y表示输出矩阵，上标t表示矩阵转置，上标-1表示逆矩阵。

上述矩阵运算量较大，利用matlab提供的函数求解矩阵转置、逆矩阵并进行矩阵乘法运算。

选择h矩阵的前p行、p列构成hankel矩阵h1，采用matlab中的svd函数对矩阵h1进行奇异值分解，分解公式如下：

h1＝vγ²u^t，

式中：γ是对角矩阵，对角元素是h1的奇异值，v、u是正交矩阵。

奇异值的大小决定了对应阶次的状态的重要程度，当奇异值很小时，对应的状态可以忽略。因此，假如大于门限值的奇异值个数为k，则模型阶次即为k。

⑤确定模型状态方程

离散时间系统状态方程为：

xi+1＝axi+bui

yi＝cxi，

其中，a、b、c为待求解矩阵。

模型阶次k确定后，从第一个元素开始分别取v矩阵的k列、u的k行和γ的k行k列构成新的矩阵v、u、γ，选择h矩阵的2～k+1行、2～k+1列构成hankel矩阵h2,令p＝vγ,q＝γu^t，则a＝p^-1h2q^-1，b为矩阵q的第一列，c为p矩阵的第一行。

利用matlab实现上述矩阵运算，确定矩阵a、b、c后，即可得到辨识模型的状态方程，进一步地，状态方程可以转换成传递函数形式。

以下为另一个实施例。一种动中通天线系统辨识方法，其针对小口径动中通天线系统进行系统辨识，包括如下步骤：

①辨识激励信号生成

系统辨识采样时间为0.01s，伪随机序列信号长度2047，重复周期4，信号幅度2(°/s)，采用matlab程序生成的伪随机序列,共计8188个点的时间序列，在生成的伪随机序列的开始和结尾插入500个点的零速数据，将生成的新数据序列作为辨识输入。

根据电机减速比、齿轮传动比，将天线辨识输入速度折算成电机驱动器速度，在and5436半实物仿真机中运行程序，辨识输入速度通过can总线发送到电机驱动器，控制电机按照给定速度转动。

伪随机序列通过编写m文件实现，将伪随机信号转换成时间序列，利用simulink搭建速度折算模块、can通信模块。

②辨识数据采集

在and5436仿真机中设置can总线接收模块，接收天线方位轴码盘数据、俯仰轴码盘数据，根据码盘位数和标校零点，将码盘数据转换成方位角度、俯仰角度，运行and5436辨识软件，启动辨识，软件发送伪随机序列给驱动器，天线转动，同时采集记录天线的给定速度、方位角度、俯仰角度，记录时间间隔10ms，辨识结束后自动停止记录。

③确定模型阶次

根据辨识输入输出矩阵定义，将预处理后的输入输出数据代入到矩阵中，得到辨识输入输出矩阵。

根据离散状态方程脉冲响应，解算h矩阵，输入hankel矩阵阶次p，提取h矩阵的前p行、p列元素构成hankel矩阵h1，利用matlab的svd命令对h1矩阵进行奇异值分解，得到矩阵v、u、γ，矩阵γ为对角矩阵，其对角元素的开方即为矩阵奇异值，奇异值门限为0.05，判定大于门限的奇异值个数k，得到系统模型阶次。

上述功能均可通过在matlab中编写的m文件实现。

④确定状态方程矩阵

模型阶次k确定后，从第一个元素开始分别取v矩阵的k列、u的k行和γ的k行k列构成新的矩阵v、u、γ

利用matlab计算矩阵p＝vγ,q＝γu^t，提取h矩阵的2～k+1行、2～k+1列构成hankel矩阵h2，则a＝p^-1h2q^-1，b为矩阵q的第一列，c为p矩阵的第一行。

矩阵a、b、c确认后，即可得到天线的离散状态空间模型。此外，根据matlab的tf2ss命令，可将模型由状态方程转换成传递函数形式。

总之，本发明是一种将待测天线接入系统后，给定天线伺服系统激励信号，采集记录响应信号，从而自动计算天线模型阶次、确定模型状态方程的辨识方法。其具有使用操作方便，辨识模型阶次确定、辨识精度高的特点，是对现有技术的一种重要改进。